联想解题“促”自然 创造编题“显”深度
——2021年浙江省杭州市数学中考第16题的解法与创编探究
姜琴娣
(余杭区黄湖镇中学,浙江 杭州 311118)
在2021年各省各地的数学中考试题中,精彩“好题”层出不穷.“研题”不仅给我们带来无限的思维冲击,而且也给予我们无穷的乐趣享受,这必然能促进教学.细研浙江省杭州市数学中考第16题——填空压轴题,发现近6年来一直延续“折叠”题,“年年考,年年新”形成一种特色,已成为一道亮丽的风景线.现以2021年浙江省杭州市数学中考“折叠”题的拓展探究为例,探讨联想解题能力的培养、深度编题的策略,与同行们共享.
1 原题呈现简析
例1如图1,在一张矩形纸片ABCD中,点M是对角线AC的中点,点E在边BC上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,联结DF,EF.若MF=AB,则∠DAF=______ °.
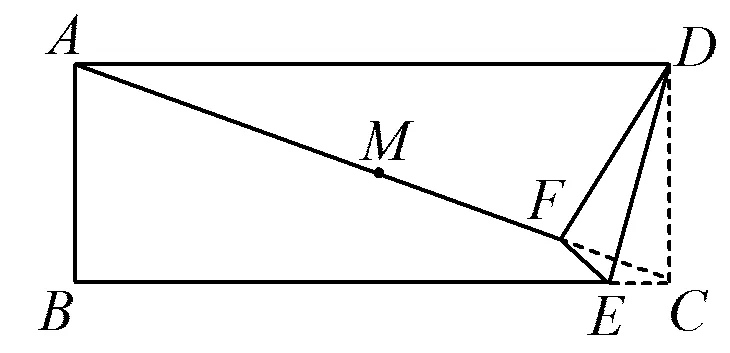
图1
(2021年浙江省杭州市数学中考试题第16题)
命题者图画得精确,解题者量得精准,得到所求角的度数为18°,而且不设“陷阱”,可谓“秒杀”.经过简单推理,果然答案如此,让优等生有“简单得怀疑人生”的感觉,中等生有“压轴题做得真爽”的感受,后进生有“竟然用量角器都能做对”的感叹.
若命题者“故意”将图画得不精确一点,仅凭“量”解决不了问题,则又与实际不符,这是不严谨的,而且会使“魅力”黄金分割之美黯然失色.
由此看来,与以往相比,此题确实难度不大,没有上演压轴大戏,也因区分度不够而略显遗憾.但题目背景简约熟悉,知识常规中矩,图形蕴涵“0.618的美丽”,其实是一道值得细细品味、深度研究的“好题”.
2 联想解题探究
在教学中,追求“一题多解”,寻求适合学生自己的“最优解”,必定能挖掘题目的潜在价值,激增学生的思考容量,有效拓展学生数学思维的宽度,培养数学解题的知识联想能力,缩短数学思维的长度.
在本题中,对于条件“点M是对角线AC的中点”可以联想到:直角三角形“斜中线”定理、等腰三角形“三线合一”性质、三角形中位线定理、倍长(类)中线法、平行四边形的对角线互相平分等,于是非常自然地作出辅助线:如图2,联结DM(或联结BD).

图2
解法1借助“共边等腰三角形”联想.
易得到等腰三角形△AMD,△MFD,△FDC,设∠DAF=x,则
∠FMD=∠FDM=2x,
进而
∠DFC=∠DCF=4x.
于是在Rt△ACD中,
∠DAC+∠ACD=90°,
即
x+4x=90,
解得
x=18,
故
∠DAF=18°.
评注结合矩形的性质、折叠、直角三角形斜中线等知识,综合运用3个“共边等腰三角形”,问题迎刃而解.
解法2借助“母子等腰三角形”联想.
易得△MCD,△MFD,△FDC为母子等腰三角形,联想到“黄金三角形”,可得∠CMD=36°,又根据△AMD是等腰三角形,利用外角性质可得∠DAF=18°.
评注根据母子相似三角形进行“巧妙转移”视线,利用“黄金三角形”直接获解,解题思路非常简捷高效.
解法3借助“轴对称列方程组”联想.
设∠DAF=x,∠CDE=y,因为∠ADF+∠CDF=90°,∠DFC+∠FDE=90°,所以得方程组
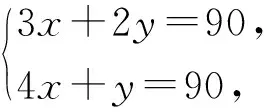
解得
x=18,y=18,
即
∠DAF=18°.
评注充分利用轴对称列出方程组顺利求得答案,达到了“左右逢源”的效果.
解法4借助“母子直角三角形”联想.
由折叠可知DE⊥AC,交AC于点N,又
∠ADC=90°,
于是
△ADN∽△DCN∽△ACD,
从而
∠DAF=∠CDE.
设∠DAF=∠ADM=x,则
∠DMF=∠MDF=2x, ∠FDE=∠CDE=x,
由于 ∠ADM+∠MDF+∠FDE+∠CDE=90°,
即
x+2x+x+x=90,
解得
x=18,
故
∠DAF=18°.
评注观察到“母子相似”就能迅速实现战线统一,解题的核心素养得以充分展现.
本题中的折叠问题涉及两个“熟悉”的模型:
1)“鸡爪”模型.如图3,MA=MD=MC(一个顶点引出的3条线段叫做“鸡爪型”线段).
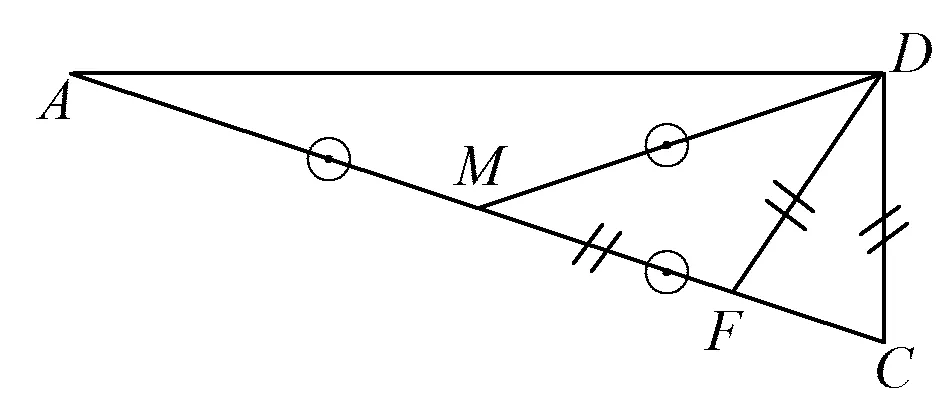
图3
2)“三节棍”模型.如图3,CD=DF=FM(一条线段连接另两条线段组成的图形叫做“三节棍”图形).
解题时,需要将图形适当、恰当地分离,概括、提炼出特殊模型(识模),借助模型可以联想到相应知识(用模),进而解决数学问题(解模),促进学生数学解题的自然生成.
3 创新编题策略
“知识求联,方法求变”,对试题进行有效变式拓展,有利于进一步感悟“母题”的解法,理解问题的本质,训练数学思想方法,不断提升分析、思考、研究问题的思维能力[1].在实际的教学“题组演练”过程中,教师积极采用“三十六计”策略,乐此不疲,精彩之技不容错过,同时让学生学会举一反三,远离题海战术,助推初中数学核心素养的培养.
创编策略1瞒天过海,化“静”为“动”.
例2图4是一张矩形纸片ABCD,点M是对角线AC的中点,点E在射线CB上,把△DCE沿直线DE折叠,使点C落在直线AC上的点F处,联结DF,EF.当FM=AB时,∠DAC=______°.

图4 图5
评注例2提供一个参考图,给学生展现空间想象的机会,将“静”的原图“动”起来,边AB仍静止,把边CD水平向右拉伸得到图1(18°),或水平向左压缩得到图5(54°).考查学生“分类讨论”思想的运用,“瞒天过海”,解题思路与原题完全不同,学生自行作出图形,尽管“测量法”仍适用,但难度上骤然提升,同时也增添了“数学味”.
创编策略2偷梁换柱,变“显”为“隐”.
例3如图1,在一张矩形纸片ABCD中,点M是对角线AC的中点,点E在边BC上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,联结DF,EF.若MF=AB=2,则AC=______.
评注例3将原题“求角度”改为“求长度”,在一定程度上提升了难度.原题所求角度显性18°被隐藏,“偷梁换柱”后联想不到36°,进而联想不到“黄金三角形”,往往会与“妙法”擦肩而过.此题若利用方程思想去解则不太容易.
创编策略3明修栈道,引“暗”变“明”.

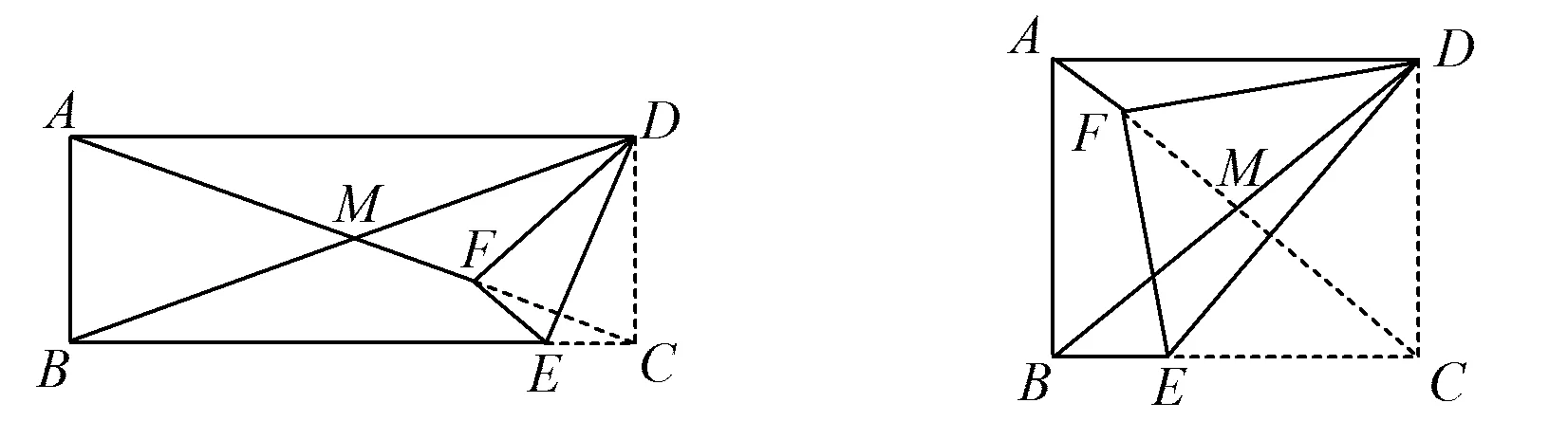
图6 图7
评注例4将条件“点M是对角线AC的中点”改为“对角线AC,BD相交于点M”,实现知识转向,将暗知“直角三角形斜中线”变为明知“矩形对角线互相平分”.给定“图6和图7”,呈现明确的两种情况,变为“明修栈道”,着重考查学生的数学思想运用能力.
创编策略4声东击西,由“近”及“远”.
例5在一张矩形纸片ABCD中,AB=12,点M是对角线AC的中点,点E在射线CB上,把△DCE沿直线DE折叠,使点C落在直线AC上的点F处,联结DF,EF.
1)如图8,当F为MC的中点时,AD=______.
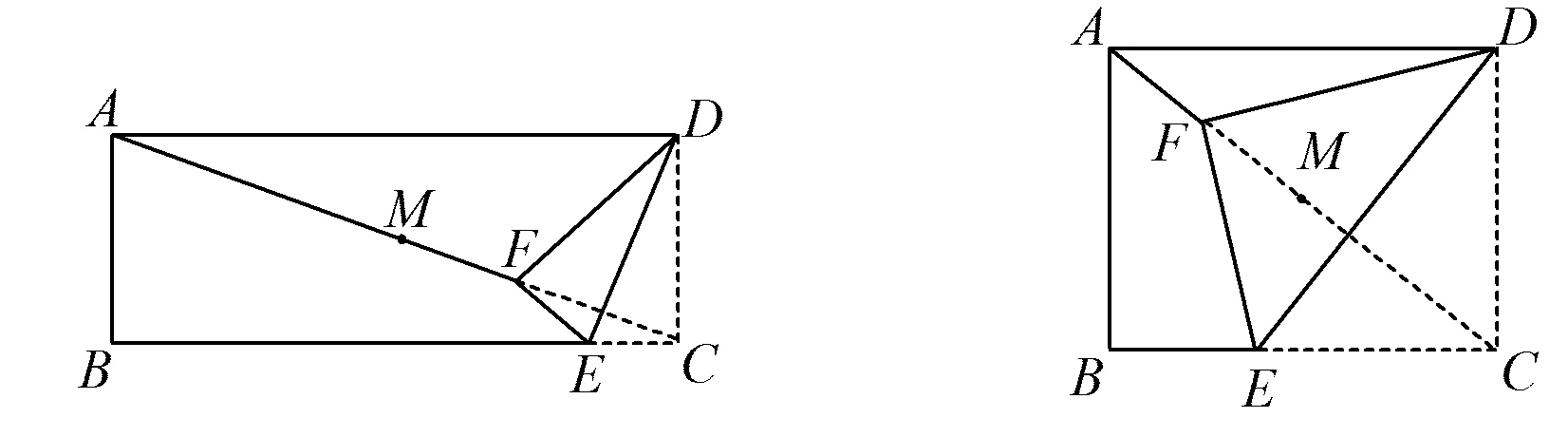
图8 图9
2)如图9,当F为MA的中点时,AD=______.
评注本改编考查“分类讨论”思想相关知识的运用.为了分散画图技能的难点,设置两个小题,给出了图8和图9,意图是为了降低难度,节省解题时间.第1)小题的“声东”为第2)小题的“击西”提供知识支架,让学生拾级而上,难度适宜,达到了由“近”及“远”的效果.
创编策略5围魏救赵,避“实”就“虚”.
例6在一张矩形纸片ABCD中,AB=12,点M是对角线AC的中点,点E在射线CB上,把△DCE沿直线DE折叠,使点C落在直线AC上的点F处,联结DF,EF.如图10和图11,当F为AC的三等分点时,AD=______.

图10 图11
评注例6给出图10(“赵”)和图11(“魏”),不同活动经验的学生的解题能力在“围魏救赵”计策下显露无遗,要救“赵”,不妨先围“魏”,避实就虚,击中要害,左右逢源,运筹于帷幄之中,呈现一定的压轴信度.当然,如果不给予一个备用图(图10和图11),那么本题彻底压轴,“画图,推理,运算”三技共舞,难度系数瞬间提高,随之也提升了区分度,但在目前“双减”背景下,不宜出一些过难之题.
4 解编教学启示
教师需关注解题“解”得精彩,更需注重编题“编”得精致.其实二者是相辅相成的,值得教师尽力探索、极力尝试、倾心渗透、潜心研究.
4.1 联想“促进”自然
“联想是思维的翅膀,解题离不开联想”.近几年浙江省杭州市数学中考试题都有意避开套用“模型”,考查的是数学本质,学生必须凭借对数学的理解,临场发挥解决问题[2].
在教学中,教师要重视基本活动经验的积累,让学生先行,呈现思考过程;要加强知识“联想”的训练,让学生善于“联想”.教师要围绕数学本质进行总结和归纳,长此以往必然会对提高解题能力、优化思维品质大有裨益,从而促进学生自然解题.
4.2 创编“彰显”深度
深度学习意味着学生需主动地参与知识的构建,获得良好的可迁移的认知结构,能综合应用和灵活运用所学知识解决问题[3].
正如本题采用化静为动、变显为隐、引暗变明、由近及远、避实就虚等创新编题策略,以核心素养为基点、能力立意为基准、数学思想为基线、活动经验为基调,从而彰显学习的深度.
总之,在几何复习课教学中,由于落实“双减”的需要,教师只有多思考、多研题、多拓编,同时必须适当考虑难度的控制,进行精准的知识关联和整合,才能充分拓宽学生的视野,夯实学生的基础知识,迁移自然解题能力,演进和内化学生的数学核心素养.

