洞察图像特征 聚焦思维卡点
冯双婕, 苗孟义
(慈溪中学,浙江 慈溪 315300)
在研究各类试题时,总能发现与函数图像有关的考题,有时考查函数图像的作法与变换,有时考查函数解析式与图像之间的相互识别,有时考查函数图像在压轴题中起着转化与化归的作用,总之依托图像特征,借助数形结合,可以快速实现精准解题.教材是一个很好的命题源泉,分析挖掘教材,是命题的生长点,也是有效备考复习的生长线,抓住这条线,可以减轻学生的负担,实现精准备考、高效复习.
1 研读教材,提炼生长线
在教学中落实并提升学生的核心素养,关键是根据学生的实际情况、新课程标准,及时找出并设计出核心素养的“生长线”,“精准”实施教学,使学生的核心素养得到“孕育”和“生长”.何为核心素养“生长线”?它是指符合学生认知规律和教学规律的实施路线和发展方向,是用数学学科思维和观念指导教学设计、反思教学的过程,是不断提升关键问题、优化关键环节、实施精准到位的系统线、科学线.
函数解析式与图像之间的相互识别是历年高考、重大考试中十分常见的题型.但不少考生无缘这类题型,是什么原因造成失分,是考点知识不够清晰还是解决方法未能掌握?浙江省教研课题“构建高中数学课堂核心素养‘生长线’的实践与研究”组在笔者所在学校开设研讨课,围绕这个问题开展讨论,找原因,想对策,重落实.笔者结合核心素养“生长线”围绕函数图像开展课例研究,就人教A版高中《数学(选修2)》第五章“一元函数的导数及其应用”中第95页的例7进行设计与讨论:
引例给出函数f(x)=(x+1)ex.
1)判断函数f(x)的单调性,并求出f(x)的极值;
2)画出函数f(x)的大致图像;
3)求出方程f(x)=a(其中a∈R)的解的个数.
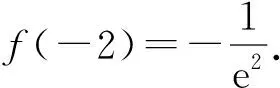
2)函数f(x)的大致图像,如图1所示.

图1
3)方程解的个数等价于y=f(x)与直线y=a的交点个数,由图1可知:
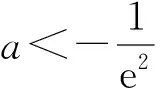
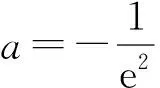

本题的教学功能是让学生体会并掌握根据已知函数的解析式进行基本性质的分析与确定,再结合得到的结果能大致绘制函数的图像.教学价值在于函数图像能直观地反映函数的基本性质,同时函数的基本性质也能刻画函数的大致图像,这种能力体现蕴藏着水平层次的差异与区分,在选拔性考试中往往比较流行,进一步提炼函数的基本性质与函数的大致图像之间的关联.这其实是一条核心素养的生长线.
2 以生为本,精准施教
根据函数的解析式识别函数图像,往往有两类题型:一类是不含参数的函数解析式,另一类是含参数的函数解析式.关键要善于发现函数解析式的基本初等函数模型、组合结构、图像特征以及参数对解析式及图像的影响,要关注选择题解题策略的高效性.
类型1不含参数的函数解析式与函数图像的相互识别.
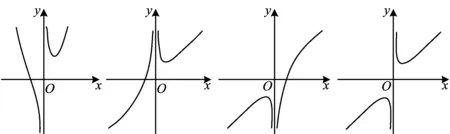
例11)函数f(x)=(x2-x)ex的图像大致是
( )
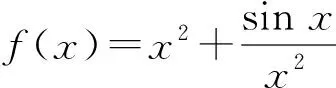
( )
1)方法1由于f′(x)=(x2+x-1)ex,令f′(x)=0,则
x2+x-1=0,
解得
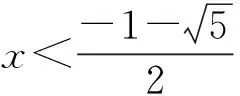
又当x<0时,ex>0,x2-x>0,从而f(x)=(x2-x)ex>0,可排除选项C.故选B.
方法2不妨设g(x)=x2-x,h(x)=ex,则
f(x)=g(x)·h(x).
令f(x)=0,则x=0或x=1,函数f(x)有且只有两个不同的零点,可排除选项A,C.当x→-∞时,g(x)→+∞,h(x)→0且h(x)>0,则f(x)→0且f(x)>0,可排除选项D.故选B.

f(-x)≠f(x),
且
f(-x)≠-f(x),
f(x)既不是奇函数又不是偶函数,可排除选项D.当x→0+时,x2>0,sinx>0,则f(x)>0,可排除选项C.当x→-∞时,x2→+∞,-1≤sinx≤1,则f(x)>0,可排除选项B.故选A.

A. B. C. D.
A. B. C. D.

可排除选项C.又
可排除选项B.故选A.
设计意图问题1)以两个函数相乘的形式呈现,与引例形式相似,问题2)以基本初等函数的四则运算相结合.问题1)的卡点在x<0时,不清楚图像的变化趋势及有无零点,方法1需求导数得到函数单调性后才可明确函数图像的大致变化趋势,方法2从函数零点的个数入手,可排除选项A,C,不难发现选项B,D在y轴右侧图像相似,需比较y轴左侧,极限思想是小题小做中的首选策略.问题2)的卡点在于不太容易用求导判断函数的单调性,用极限思想快捷精准.
例2已知函数f(x)的大致图像如图2所示,则该函数的解析式可能是

图2
( )
A.ex·ln|x|
C.ln|x|+ex
D.ex-ln|x|

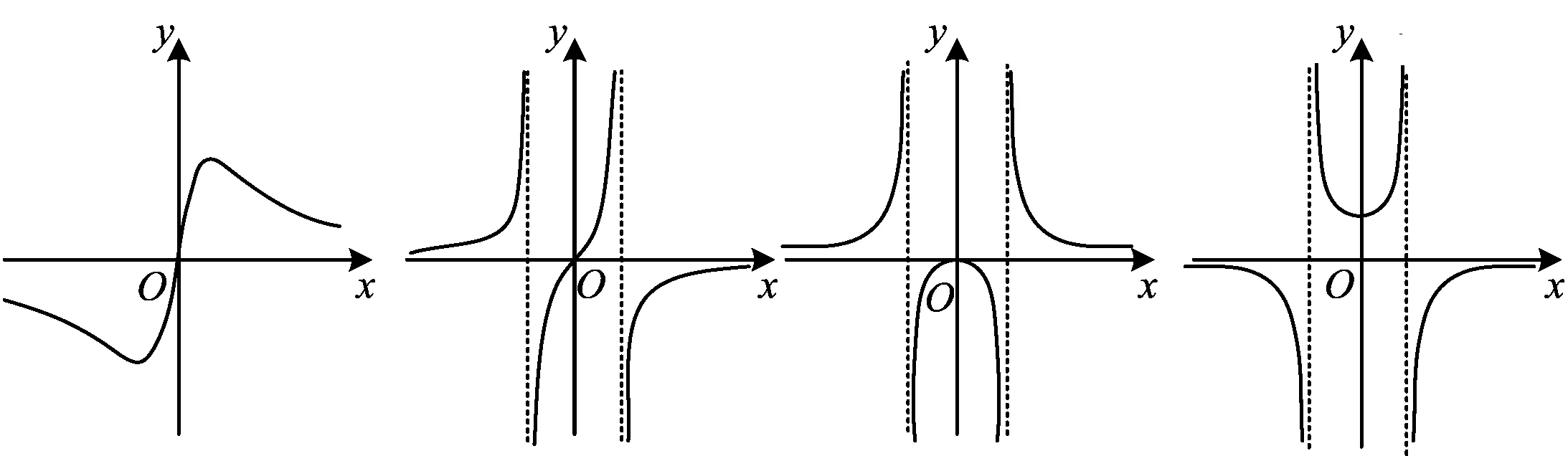
A. B. C. D.

类型2含参数的函数解析式与图像的识别.

( )



综上所述,选项A,B,D正确.

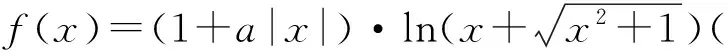
思考同一平面直角坐标系内函数f(x)与f(x-a)的图像的位置关系、零点问题,不等式取值范围等.
类型3先变形后作图.
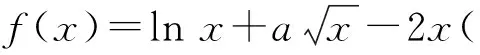
1)求实数a的取值范围;


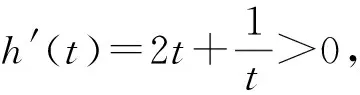

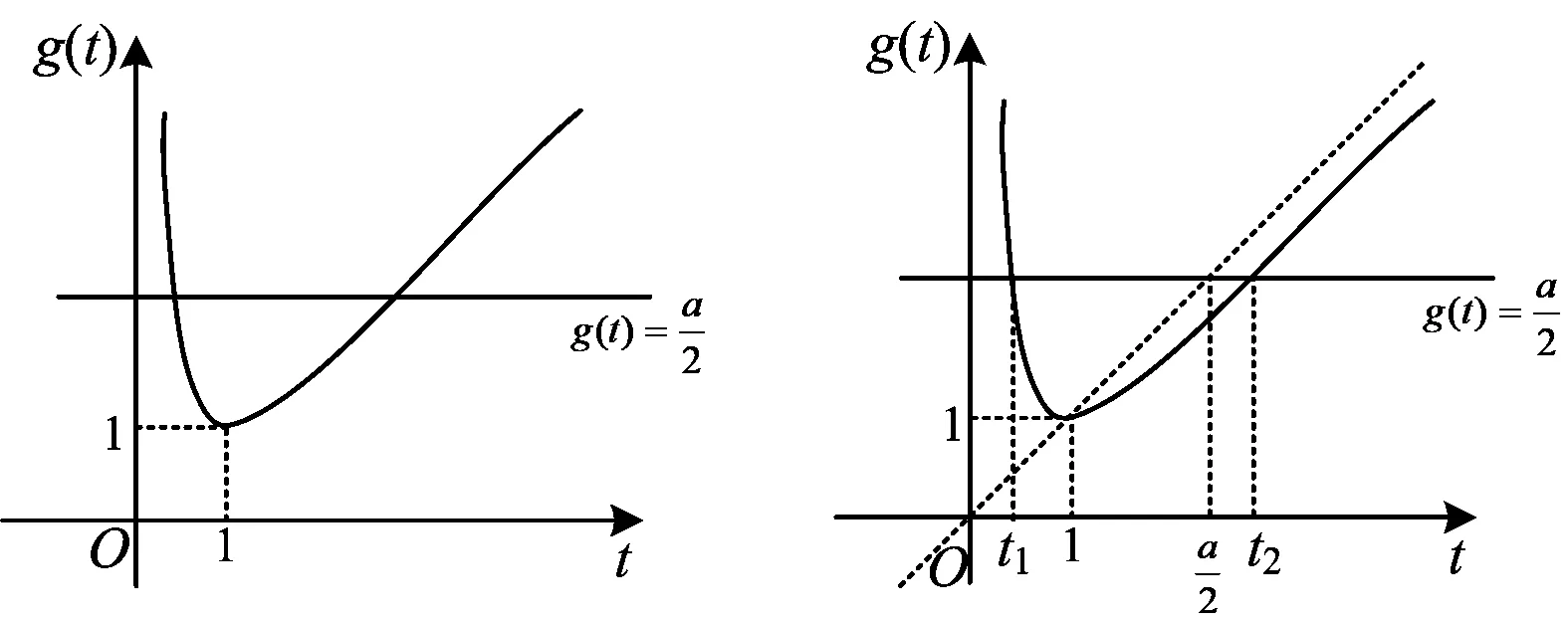
图3 图4
注意到当t>1时,
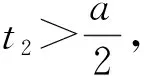
由第1)小题知0 即 下面证明t1t2>1. 从而函数h(t2)在区间(1,+∞)上单调递减,于是 h(t2) 即 故 得 t1t2>1. 因此 即 设计意图有些不含参数的函数图像是容易画出的,有些含参数的函数图像不能直接画出.本题的思维卡点在于不能直接求出最大值点,通过数形结合发现需将参数分离出去,但并非每一道题都可以通过分离参数来解决,分离参数的核心思想是“简化解题”,强调图像是否能反映问题的关键信息.换元是一种技巧,其初衷依旧是使问题解决得到简化,经过转化,构造函数将双变量问题转化为单变量问题来处理. 核心素养的“生长线”具有针对性、适应性、生成性、实效性的特点,将教材中的例题、习题、复习参考题的教学价值与功能发挥到最佳,是核心素养得以有效落实的保障.课堂例题的选择,教学功能、价值的体现,问题自我解决能力的培养,是核心素养的“生长线”形成的重要因素.追溯课堂教学中所呈现的3种类型的例题,其模型组合、内容特征、策略方法值得关注. 1)丰富的模型与组合:教材中的f(x)以g(x)·h(x)形式呈现,即两个函数相乘型,当然也可以通过相除、相加、相减、复合,或者是分段函数、取绝对值函数、取最值函数;两个函数g(x),h(x)又有各自的形式,如正比例函数、反比例函数、一次函数、二次函数、对勾函数、飘带函数、指数函数、对数函数、三角函数等,都是学生熟悉的基本初等函数模型. 2)核心的内容与特征:无论函数呈现的模型、组合如何变化,需要考查的核心内容与特征大致相同,即要关注函数的定义域、值域(最值)、单调性、奇偶性、对称性、周期性、零点、渐近线等,进行平移变换、对称变换,要善于抓住图像的特征并结合函数的基本性质进行问题的解决. 3)最佳的策略与方法:观察函数的图像,寻找切入点,要善于捕捉特殊点、线(如f(0)、定点、定线、零点、拐点、渐近线)代入检验与排除,要会根据函数的三要素(主要是定义域)和性质(单调性、奇偶性、对称性、周期性)等检验与排除,能运用函数的定义域与值域(图像的左右位置、上下位置)、函数的奇偶性(图像的对称性)、函数的单调性(图像的变化趋势)、函数的周期性(图像的循环往复)函数的特殊点和线(定点、定线、渐近线),结合特殊值法、估算法、排除法进行求解.用极限的思想来分析是这类试题的撒手锏,当x→0+,x→0-,x→+∞,x→-∞时,3类函数增长速度对比,指数暴涨:指数函数>幂函数>对数函数. 如何精准检测并有效反馈课堂教学,编制一份有针对性的课后作业进行独立检测很有必要.可以结合课堂互动中所反映的学生的所思所虑,有针对性地设计问题、编制作业;可以在学生思维的最近发展区,编制学生课外能独立解决的问题、作业;课堂例题不能只有单一的练习功能,不能只设计形式单一、简单重复、直接套用的练习,可以结合学情、围绕所学基础知识设计一些符合学生认知水平与思维水平的问题链,从而不断提升关键问题的设计、优化关键环节的预设、有效地精准实施.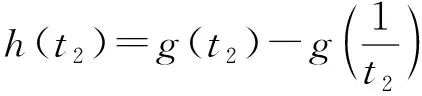
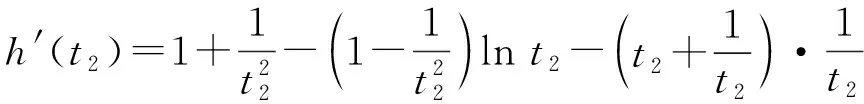

3 精准测评,有效反馈

