例谈基于数学发展内在逻辑的教学及价值

李福军, 戚颖朵

(1.宁海海亮学校，浙江 宁海 315600;2.海亮初级中学，浙江 诸暨 311800)

每门科学都有推动自身发展的内在逻辑，数学也不例外.数学源于生活的外显属性，导致教学中忽视了学科发展的内在逻辑，殊不知“数学的精神、思想和方法却是创作数学著作、发现新的东西，使数学得以不断向前发展的根源”[1]，我们暂且把这种推动力称之为数学自身发展的内在逻辑！

1 数学发展内在逻辑的主要表现

一般认为，矛盾是推动事物发展的内在动力，而数学内部的矛盾是促使数学发展的最主要的内在逻辑，主要表现在以下4个方面.

1)数学的应用化、合理化过程中的自洽性问题.

数学从开始的少数几个公理出发，进行符合逻辑地推导，证明出定理、公式，又导出另外的定理、公式.例如欧氏几何就是通过先建立公理体系，再引进新的定义和概念，在应用和合理化推广过程中解决一系列自洽性问题，最终搭建起的庞大的逻辑体系.

2)数学的扩张化、一般化过程中的普适性问题.

数学中许多概念，从最初的原始状态不断扩张，伴随着一般化过程中普适性问题的解决，最终形成广泛而精确的概念.例如函数的概念，就是通过7次扩张，直到成为今天这样令人惊叹的广泛的概念.

3)数学的组织化、系统化过程中的统一性问题.

早期的数学都是零碎、片断的，而随着数学的发展，最后通过组织化形成一个系统.例如：自然数是由计数的需要产生的，分数是由表示等分物品的需要而产生的，无理数是由开不尽方的需要而产生的，负数、复数是由求解方程的需要而产生的……数系的扩充很好地诠释了矛盾推动数学前进，又通过系统化过程形成统一体.

4)数学的严密化、形式化过程中的严谨性问题.

很多数学知识都是精神研究的产物，因而会出现一些与现实经验相违背的知识版块，最典型的就是被视为“异端”的非欧几何，正是因为有违常识的矛盾，所以要通过引进假设，进行严密的形式化推演，最终形成严谨的知识体系.

2 基于数学发展内在逻辑的教学实践

教学中应体现数学内在发展的逻辑，但教科书只以文本的形式呈现了最终的知识，而教学者要做的事就是挖掘学科内在的逻辑，通过“再创造”还原数学知识“火热的思考”.基于上述分析，笔者从以下4个方面进行了教学尝试：

2.1 注重知识的整体性把握

数学的最大特点是整个知识像是一张网，相互关联而不能割裂，教学中要强调知识从哪里来到哪里去，要形成对知识的整体性把握.

案例1浙教版《数学》七年级上册第2.1节有理数加法(1).

针对教材中过于文本化的呈现，可设计以下问题串：

1)加法是求和，和是有理数，可以分成哪两个部分？

符号和绝对值.

2)如何确定和的符号和绝对值？

借助数轴，分同号和异号两数相加的情况得出法则，强调先确定符号再确定绝对值.

3)计算(+2)+(-2)=？

异号两数相加，但绝对值相等，法则有漏洞，探究后补充：互为相反数的和为0.

4)再计算(+2)+0=？(-2)-0=？

这里0没有符号，原法则不能解决，需再次进行补充规定……

5)谈谈有理数的加法与小学算术数的加法的异同？

评注教材往往把知识以符合文本逻辑的形式呈现，而教学应把知识按学科内在发展的逻辑并符合学生的认知规律进行重组，即符合教学的逻辑呈现，关键要把握学习的路径：探明知识生长点—新的问题(并解决)—次生问题(打补丁解决)—构建知识网络—进入下一新的学习内容…….本节课的逻辑循环具体表现在：

1)知识生长点：相反意义的量、有理数、数轴、算术数的各级运算，这里最关键的是要理解有理数是由符号和绝对值两个部分组成；

2)新的问题：如何处理有符号的数的加法，即有理数相加，要遵循从简单到复杂，先同号再异号；

3)次生问题：法则表面上解决了问题，但又产生新的问题，如何打补丁，最终完成一个自洽的体系；

4)构建知识网络：如何与原有的知识进行有机融合；

5)进入新的学习：有理数的减法、乘除法又如何进行；

……

2.2 注重结论的推广性拓展

许多数学上的伟大成果都是在对结论的推广性拓展中产生的，如费尔马大定理就是对勾股定理进行拓展的猜想，再经过数代数学家不懈的努力解决，这也是推动数学发展的重要内在逻辑.

案例2如图1，在△ABC中，AB=AC,P是BC上任意一点，过点P作PE⊥AC,PF⊥AB，试问：PF+PE的和为定值吗？

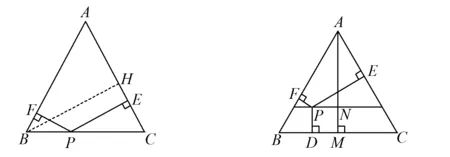
图1 图2

拓展1上述结果可以得出什么结论？

等腰三角形底边上任一点到两腰的距离和等于腰上的高线长.

拓展2等边三角形边长为a，求边上任一点到另两边的距离和.

拓展3等边三角形边长为a，求其内任一点P到3边的距离和.

如图2，由PF+PE=AN,PD=MN,得PE+PF+PD=AM.

拓展4如果点P在△ABC外，又会有什么样的结论呢？

分两种情况：如图3，点P在△ABC外，可得

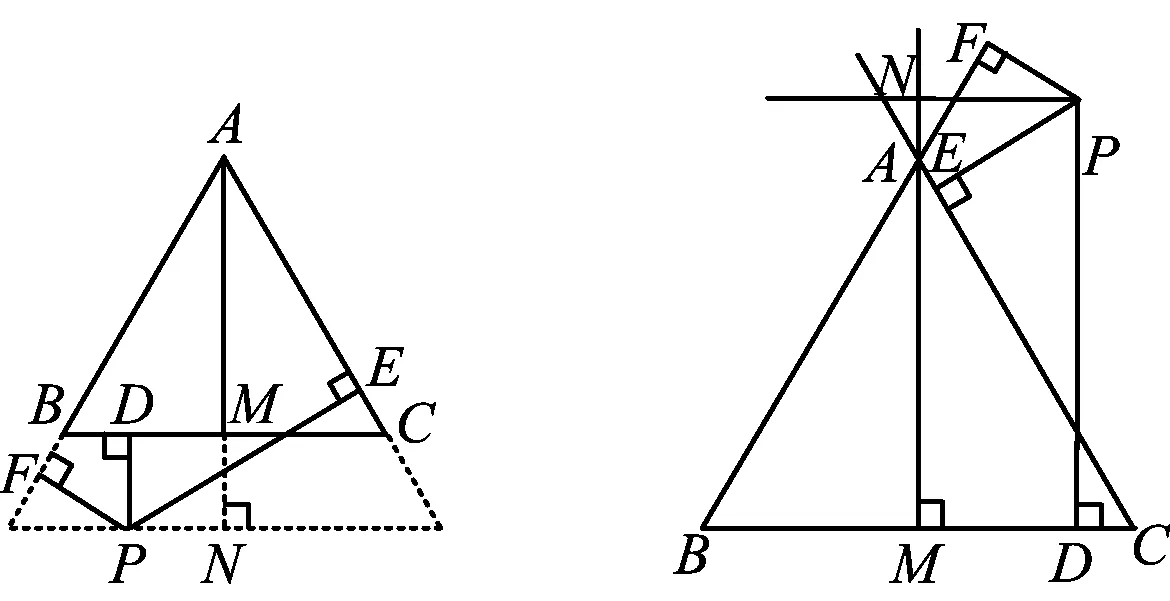
图3 图4

PE+PF=AN,AN-PD=AM,

从而

PE+PF+(-PD)=AM；

如图4，可得 (-PE)+PF+PD=AM.

结合图形，发现当垂线的方向与原始图方向相反时线段的值取负值.

结论1无论点P在何处，三垂线代数和为定值(等边三角形的高).

评注本案例通过追问学生“如果点P位于三角形的不同位置，那么结论是否成立”，极大地调动了学生的学习兴趣.当然，教学中点P的位置也可以让学生自己去设定，并自己去寻求答案，将会更精彩.

2.3 注重新知的结构化纳入

皮亚杰认为：学习的过程是“同化—顺应—平衡”的过程.数学学习也是如此，刚接受新知时，是一种同化的过程，当知识积累到一定程度后，必须通过顺应再实现新的平衡，即将新知进行结构化纳入，才能建立起牢固的知识结构.

案例3借鉴段春炳教师的教学课“同底数幂的除法”.

在最后环节，段教师进行了非常精彩的新知的结构化纳入[2].

师：我们把加、减称为一级运算，乘、除称为二级运算，乘方称为三级运算.请观察幂运算和指数运算的关系，你能得到怎样的结论？

1)am·an=am+n,幂相乘→指数相加.

2)am÷an=am-n,幂相除→指数相减.

3)(am)n=amn,幂乘方→指数相乘.

生1：指数运算比幂运算降了一级.

师：请大家再比较下面两个公式，又能得到什么结论？

4)(ab)n=anbn,乘方对乘法有分配律.

5)m(a+b)=ma+mb,乘法对加法有分配律.

生2：高一级运算对低一级运算有分配律.

师：那(a+b)2=a2+b2为什么是错的？

生3：乘方比加法高两级，不存在分配律了.

……

评注教师在法则教学后，一般只会通过例题、习题进行巩固，而段老师的高明之处在于对4种幂的运算进行比较、总结，揭示三级运算的转化关系，把新知进行结构化纳入，使学生对运算的理解更为深刻.

2.4 注重思维的严谨性训练

正因为数学中的许多成果是精神研究的产物，所以严谨性的要求比别的学科更高，在教学中必须注重对学生思维的严谨性训练.

案例4如图5，在⊙O中，弦AB∥CD，∠BAC=90°，直径EF分别与AB,CD相交于点H,I.求证：EH=IF.

图5

分析本题只需联结BC，证明△OBH≌△OCI即可.但学生往往会想当然认为BC过圆心，即想当然地认为BC是直径，这里暴露出学生思维严谨性的不足，教学中务必把握住机会，对学生进行思维的严谨性训练.

3 教学价值

遵循数学发展的内在逻辑的教学，与当下数学教学的热点高度契合，主要表现在以下3个方面：

1)关注基本活动经验的积累.

从“双基”到“四基”，是对数学教学理解的一大提升，但大家往往对基本活动经验的积累无感，其实在上述教学改进中，无不体现出基本活动经验的积累.如案例1中不断地经历出现问题、解决问题的自洽性建设(也体现出数学的严谨性)；案例2则是在变化中对结论进行不断地推广，让学生体会数学的普适性建设……由此可见，基于数学发展的内在逻辑的课堂教学，能使基本活动经验的积累融合于日常的学习之中.

2)体现数学核心素养渗透.

义务教育阶段的数学核心素养是：会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界.而重视数学发展的内在逻辑的教学无一不体现着这三大核心素养，只有深刻理解数学学科内在的发展逻辑，并按这一逻辑组织展开教学，才能让学生树立数学的眼光观察的世界观、建立用数学的思维思考的方法论，同时在实践上具备用数学的语言表达的输出能力.如案例3，在得出法则并进行了一定的熟练后，从数学思维出发，从运算的层级的角度进行思考，揭示其内在规律，让学生用数学的思维思考现实的世界；案例4则更是规范了用数学语言进行表达.

3)促进教师专业能力提升.

随着教师队伍的学历层次的提升、教师的职称评定系统日益完善，教师的专业地位已确立，但平时强调的教师专业能力往往会更多地关注教学技能、心理学和教育学等通识，数学专业方面最多会关注一些解题能力的提升，而较少对学科自身发展的内在逻辑的研究.如果教师能关注学科自身发展的内在逻辑，并能把学科逻辑与教材的文本逻辑、学生的学习逻辑相结合，形成自己的教学逻辑，这无论是对教师的专业能力提升还是对学生数学核心素养的培养都是大有裨益的.