学习要抓住本质——以立体几何距离和角的统一性为例

王 琛

(绍兴市第一中学，浙江 绍兴 310012)

学习要“抓住本质”，这是我们指导学生学习数学时经常会提到的经验.但如果深刻反思一下“什么是本质，怎样去抓住本质”，无论是学生还是教师在认识上都会有很大差距.一般我们认为：对于定义、定理、公式，不仅要熟记它们的文字表述，还要准确无遗漏地掌握它的构成，这就是抓住本质.虽然这种认识并无错误，但从《普通高中数学课程标准(2017年版)》要培养学生数学核心素养的角度看，这样对“抓住本质”的认识远远没有达到真正理想的境界.而且这样学下去，随着新的概念、知识的不断增加，记忆上会不堪重负，常常会出现学新忘旧的情况，因为这时的知识在头脑中是碎片化的，没有融为一体，这样的知识学习，对学生数学核心素养的培养，也不会有促进作用和利用价值.

那么，正确的做法是什么呢？我们认为应当从系统的角度去学习数学知识，置知识于系统之中，应着眼于知识之间的联系和规律，着眼于数学思想、数学核心素养的渗透，从而深入本质，抓住本质.这里我们以立体几何中有关点、线、面的距离和角的统一关系为例做一探究说明，希望对广大师生的教和学有所启发.

视角1立体几何中有关点、线、面的距离从两平行平面角度看是统一的，大小是唯一的，且点、线、面的各种距离，是相应点、线、面上各取任意一点的连线段长度的最小值.

立体几何中有关点、线、面定义了7种距离，即点点、点线、点面、两平行线、两异面直线、直线与平面、两平行平面之间的距离.

如图1，平面α和平面β为分别经过对应点A，B(垂足)，或直线a、直线b且和直线AB垂直的两平行平面，则从平行平面α和平面β的角度看，7种距离可以统一为平行平面α和β的距离，或两平面内任意一点到另一平面的距离，即距离值不会因为点或线在一个平面内的平移、转动变化(距离不变性)，且为相应点、线、面上各取任意一点的连线段长度的最小值.这进一步为通过转化化归思想求距离值提供了理论依据和解题路径，并呈现出了体积法、代数法、向量法等众多间接求法.

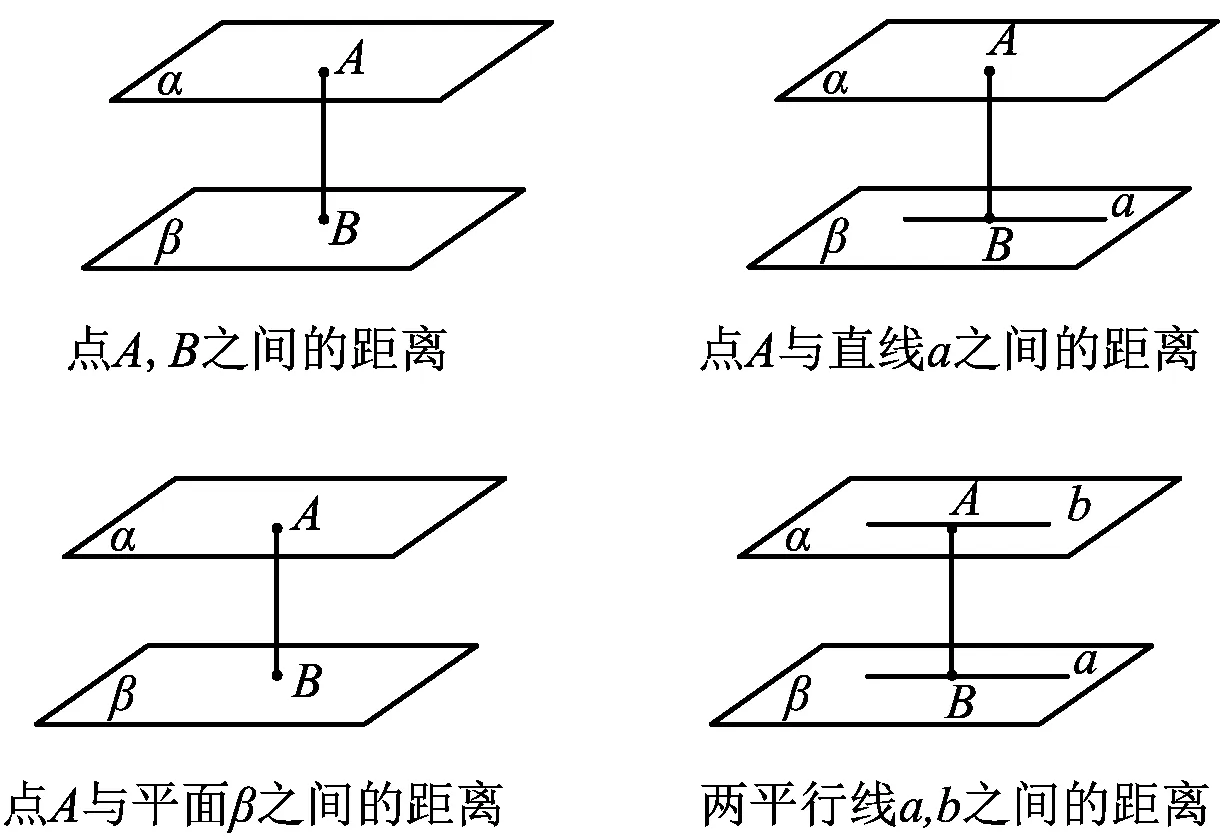
图1

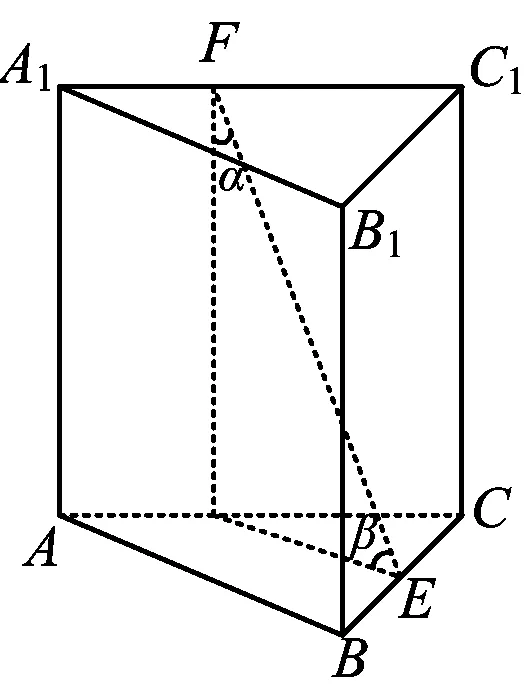
例1如图2所示的长方体木料中，已知AB=BC=2，AA1=1，设E,F分别为DD1，AA1的中点，G为线段EF上一点，则△A1GC面积的最小值为______.该长方体中经过点A1,G,C的截面面积的最小值为______.

图2 图3

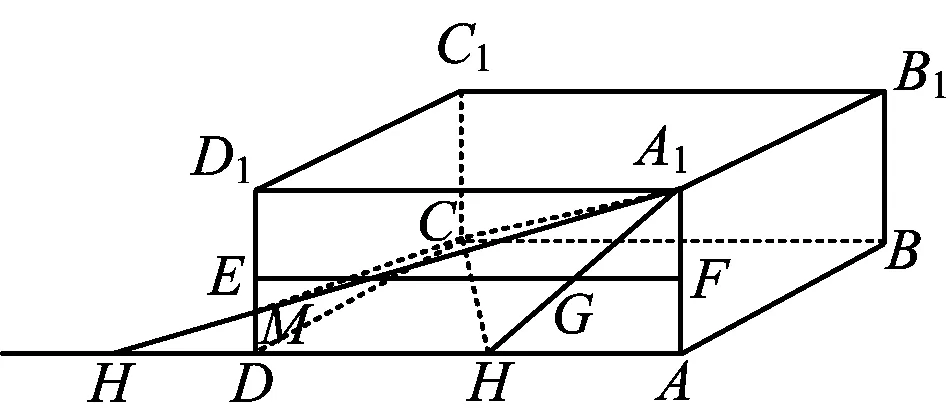
图4

说明原解通过设GE=tEF，用代数法求解，较为烦琐.若数形结合利用7种距离的等价关系思考，则可实现化繁为简.同时也可利用7种距离的等价关系拓展或改编形成如求异面直线EF与A1C、点C到面EFTS的距离等7种距离的系列试题及以下的改编题组.

图5 图6

说明基于立体几何中有关点、线、面的距离和两平行平面的统一性，我们可以将动点由线及面，从而得到改编题1，条件结合向量呈现并将定长线段设置进行调整或更为隐蔽，得到改编题2.

视角2立体几何中有关线、面之间所成的角，从二面角的平面角角度看是统一的、大小是唯一的，且线、面之间所成的角是相应特定结构中一类角的最值角.

立体几何中有关线与面之间的角，除平面几何中定义的相交直线所成角外，又定义了3类角，即两异面直线所成角、斜线和平面所成角和二面角的平面角.

如图7，平面α和平面β分别为异面直线AE,BF分别与它们的公垂线EF确定的平面，从二面角α-EF-β角度看，上述3类角可以统一为二面角α-EF-β的平面角，即异面直线AE,BF所成角的大小等于直线AE与平面α、直线BF与平面β所成角的大小，也等于二面角α-EF-β的平面角或其补角的大小，并进一步体现出角大小的“平移不变性”，即凡是与直线AE,BF或平面α、平面β平行的线或面，它们与对应的线或面所成的角和原来的大小相等.如若直线l与直线AE平行，则直线l和直线BF所成角与直线AE和直线BF所成角大小相等，直线l和平面α所成角与直线AE与平面α所成角大小相等.

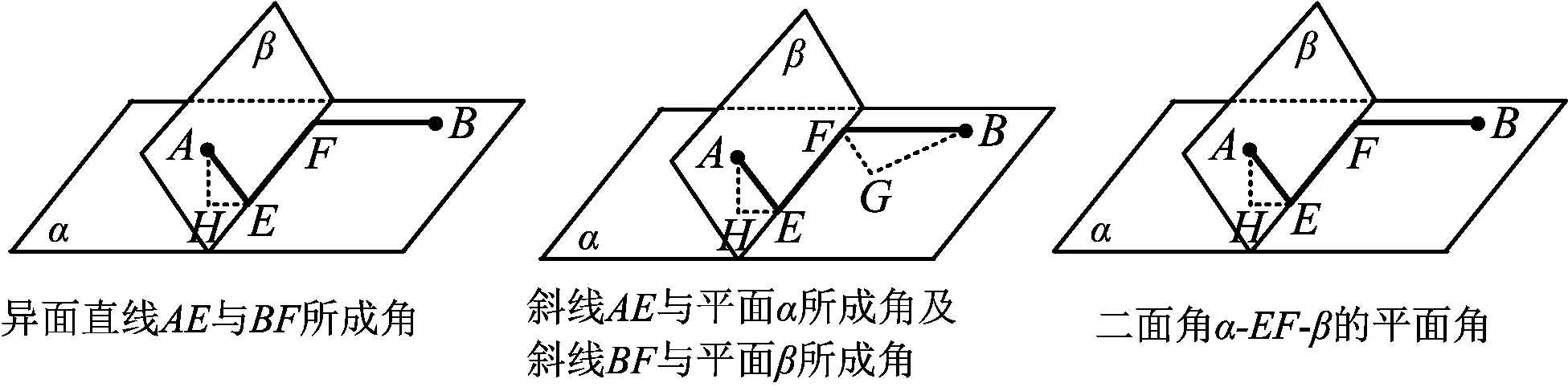
图7

角和距离类似也具有最值性，具体有最小角定理和最大角定理.

结论1(最小角定理)线面角是线线角的最小角.

如图7，对应3类角可统一表述为：直线AE与平面α所成角，或直线BF与平面β所成角(或两异面直线AE与BF所成角，或二面角α-EF-β的平面角或其补角即为非钝角的角)分别为直线AE与平面α内任一直线所成角，及直线BF与平面β内任一直线所成角中的最小角.

结论2(最大角定理)二面角的平面角是线面角的最大角.

如图7，对应3类角可统一表述为：平面α和平面β的二面角的平面角(或两异面直线AE与BF所成角，或直线AE与平面α所成角，或直线BF与平面β所成角)为平面α中的任意一条直线l与平面β所成的线面角中的最大角，也为平面β中的任意一条直线m与平面α所成的线面角中的最大角.

视角3如图8，空间线与面之间所成角的定义与点、线、面距离有着直接的关联，并有着如空间四边形AEBF等特定的结构和特点.进一步由这些结构特点，可以得到以下结论：

图8

结论3(异面直线上两点距离公式)如图8，AB2=AE2+BF2+EF2±2AE×BF×cosθ，其中θ可以为平面α和平面β的二面角的平面角，或两异面直线AE与BF所成角，或直线AE与平面α所成角，或直线BF与平面β所成角(其中EF为异面直线AE,BF的公垂线).

例2如图9,在矩形ABCD中,AD

图9 图10

( )

A．α>β>γB．γ>β>α

C．γ>α>βD．α>γ>β

分析由线面角最小角定理可知α>β,由二面角最大角定理可知γ>β.

如图10,过点D′作D′M⊥AB，则异面直线D′M和BC所成的角即为二面角D′-AB-C的平面角γ.因为BC⊥AB，所以直线BC与平面ABD′所成角也为γ，由线面角最小角定理可知α>γ,从而α>γ>β.故选D．

说明异面直线所成角、线面角和二面角的等价转换是解决问题的关键，体现了上述3类角的等量关系；利用线面角最小角定理、二面角最大角定理是解决问题的关键，体现了上述3类角的不等量关系.

利用上述3类角的统一等值关系或将锥体这一载体改变成柱体等,也可进一步改编形成系列题组.

改编1如图9,在矩形ABCD中,AD

( )

A．α>β>γB．γ>β>α

C．γ>α>βD．α>γ>β

分析直线BD′与平面ACD′所成角为β,二面角A-CD′-B的平面角为γ，由二面角最大角定理可知γ>β.因为AD′⊥D′C，所以可将二面角A-CD′-B的平面角看做AD′和平面BCD′所成的线面角，由线面角最小角定理可知α>γ,从而α>γ>β.故选D．

改编2如图9，在长方形ABCD中，AD

( )

A．α>β>γB．γ>β>α

C．γ>α>βD．α>γ>β

分析1因为AD′⊥D′C，所以二面角A-CD′-B的平面角等价于AD′与平面BD′C所成的线面角，由线面角最小角定理可知γ<α.

另一方面,在三棱锥D′-ABC中，根据几何体的对称性知直线AD′与平面ABC所成角等于直线BC与平面ACD′所成角,即直线BC与平面ACD′所成角为β.而二面角A-CD′-B的平面角为γ，由二面角最大角定理可知γ>β，即α>γ>β.故选D．

分析2因为AD′⊥D′C，所以二面角A-CD′-B的平面角等价于AD′与平面BD′C所成的线面角，由线面角最小角定理可知γ<α.

另一方面,在三棱锥D′-ABC中，根据几何体的对称性知二面角A-CD′-B的平面角等于二面角C-AB-D′的平面角,即二面角C-AB-D′的平面角为γ，由二面角的最大角定理可知γ>β，即α>γ>β.故选D．

说明要解决改编1和改编2，几何体的对称性是解决问题的突破口，线面角和二面角的等价转换是解决问题的关键，利用线面角最小角定理和二面角最大角定理是解决问题的有效工具.

例3如图11，已知正三棱柱ABC-A1B1C1，AC=AA1,E，F分别为棱BC，A1C1上的点.记EF与AA1所成角为α，EF与平面ABC所成角为β，二面角F-BC-A的平面角为γ，则

图11

( )

A.α≤β≤γ

B.β≤α≤γ

C.β≤γ≤αD.α≤γ≤β

(2022年浙江省数学高考试题第8题)

分析由二面角最大角定理可知β≤γ，因为AA1⊥面ABC，所以α与β互余且在以EF为斜边的直角三角形中.由α所对边不大于β所对边，可知α≤β.故选A.

说明例3是基于线面角最小角定理和二面角最大角定理改编而成的高考题，与例2及改编1，2相比，一是载体由三棱锥变为三棱柱，二是将3类角的等价关系通过“面的法线”转变为互余关系，进一步将线面角最小关系转变为最大关系，但本质并没有改变.

立体几何中距离和角的定义及求法，分散在新教材的两章各节，如最大、最小角定理及投影线段公式等，甚至没有在教材中单列呈现，而是隐藏在具体的习题之中.事实上，无论是距离和角的定义、求法，都是以唯一性或最值性为基础演绎出的一个统一的系统，即它们原本就是一个系统，因此距离和角的上述关系，看上去会有些令人意想不到，却是必然的合情合理.这种“置知识于系统中，着眼于知识之间的联系”的学习方法，实际是一个融会贯通的过程，能使我们通过繁杂的现象抓住本质，简化记忆.更为重要的是，这是数学核心素养培养作为目标认识问题的一种思想方法，即由寻找联系入手，运用化归等数学思想及“从特殊到一般，又从一般到特殊”等数学方法，把个别的、离散的现象构成浑然一体的系统，实质也是新教材“大单元教学”的本意，对学生能力的提高和素质的发展具有重要的意义.