高中数学习题课教学中的问题链设计——以平面向量的解题项目化教学为例

朱祖煌

(诸暨中学,浙江 诸暨 311800)

1 数学解题教学中的问题链设计

在数学教学中，“解题”教学是一种最基本的活动形式.无论是核心素养中数学抽象、逻辑推理的提升，还是通过数学运算促进和提升学生的数学思维，形成规范化分析和思考问题的品质，养成严谨求真务实的科学素养，都离不开问题链的精心设计[1].数学问题链教学不仅关注了学生基础知识与基本技能的掌握，更关注了学生对数学知识理解的深度.在问题链教学中，教师常常通过问题组织学生的学习内容，用“链”去引导学生学会思考，在教师的预设问题和学生的生成问题中评估学生的知识掌握程度和知识拓展与迁移能力.笔者在日常解题教学中，结合导问式教学方式，以数学问题为载体，以主干问题—延伸问题—提炼问题为教学组织形式，以学生辨析、师生辩驳为教学手段，引导启发学生主动思考、探讨(如表1).在问题链的解决过程中进一步引导学生提问，从而培养学生的数学学习力(知识与经验、思维与方法、批判与创新)，进而提升学生发现与解决问题的能力[2].

表1 基于提升学生数学学习力的数学解题教学原则与问题链的设计

2 以平面向量的解题项目化教学为例

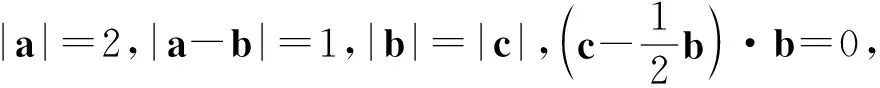
主干问题问题1～问题5.

问题1在起点问题中，描述几何关系的量有哪些？

通过审题环节，理解题中向量模长与向量数量积等基础知识点的数学含义.基于知识内容教学的主题思维设计如下问题链：

问题2-1题中的代数关系|a|=2,|a-b|=1,|b|=|c|，用几何语言如何描述？

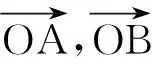
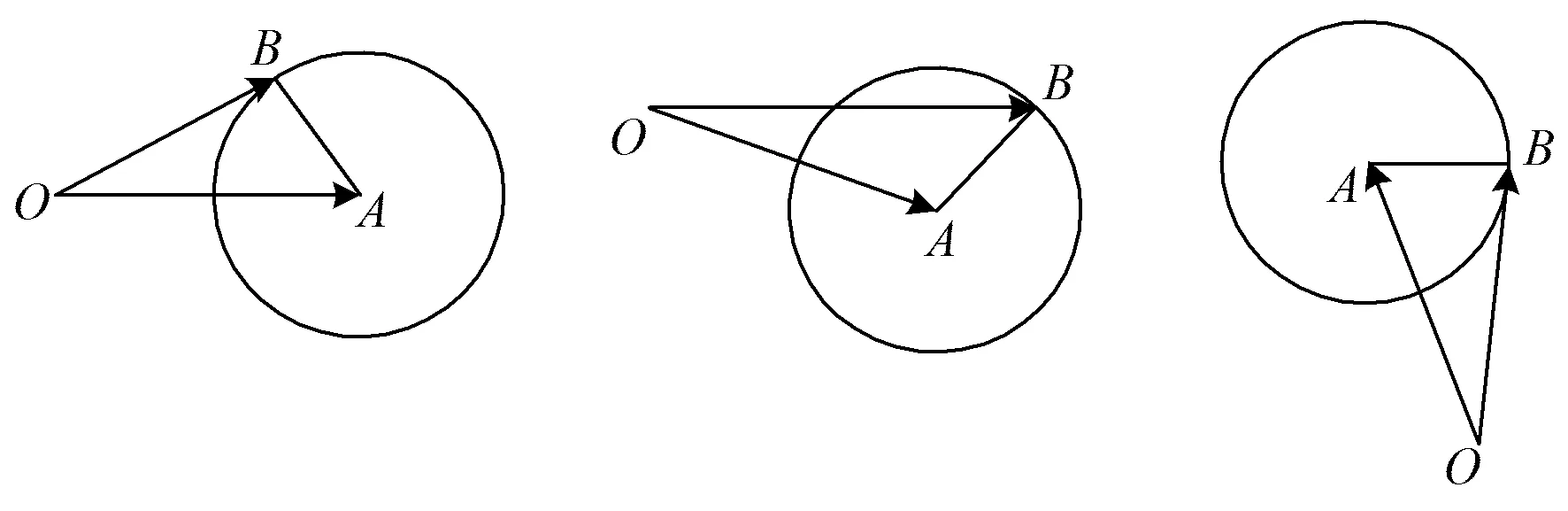
图1 图2 图3

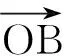
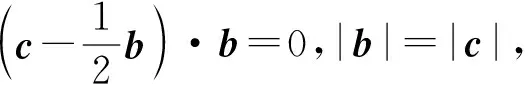
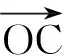
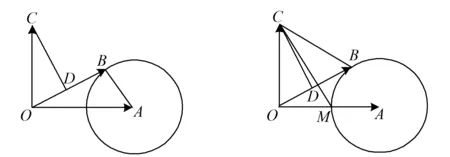
图4 图5

问题2-3(追问与辩驳)此时△OBC确定吗？为什么？

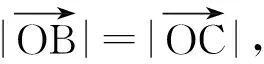
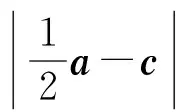
课堂预设表示点C到OA中点M的距离，即线段|CM|(如图5).

问题3-1在图6中，要求线段|CM|的最大值，其中不变的几何量是什么？与|CM|的关系如何？

课堂预设点B在⊙A上运动，且|OC|=|OB|保持不变，故点C的运动是由点B的运动而变化的.点M是一个确定的点，因此需要确定动点C的轨迹.

课堂生成如图6，|CM|≤|DM|+|CD|，且

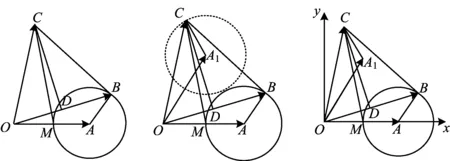
图6 图7 图8

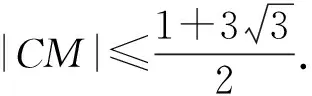
问题4-1能从几何角度出发，确定动点C的轨迹吗？

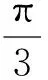
课堂生成动点B的轨迹是圆，动点C与动点B的运动相关，可以建立直角坐标系，利用求轨迹方程问题中相关点的思想确定动点C的轨迹方程，从而确定轨迹类型(如图8).

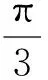
课堂预设利用复数的乘法的几何意义可以表示点B,C之间的关系.设点C(x1,y1)对应的复数为z1=x1+y1i，点B(x0,y0)所对应的复数为z0=x0+y0i，则

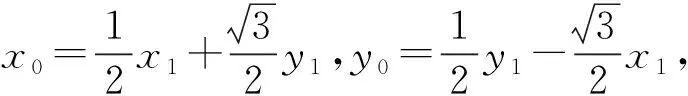
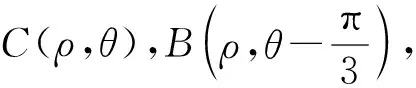
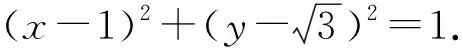
问题4-3(延伸问题1)描述动态几何中，常见的变量有哪些？

课堂预设线段长度变量x，角度变量θ.

问题5-1(延伸问题2)这样的解题策略关键点在哪里？

课堂预设在用向量法解决几何问题中，借助几何直观，用几何语言转化为向量语言，画出各个条件表征的几何元素.

问题5-2(延伸问题2)如何计算几何元素的最值？

课堂预设1)利用几何观，寻找几何元素中的变与不变量，通过转化求几何最值；2)利用代数运算，将几何问题转化为代数问题，由数形结合思想构建几何之间的桥梁.

问题6(提炼问题1)通过起点问题，你能总结解决此类向量问题的一般策略吗？

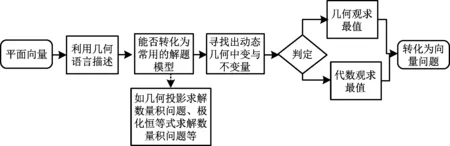
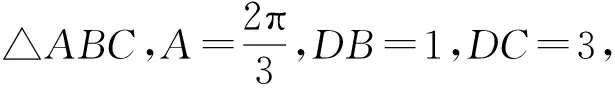
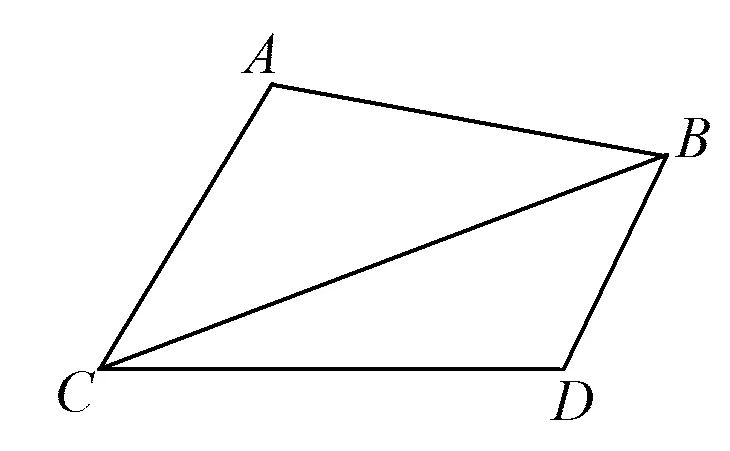
图9

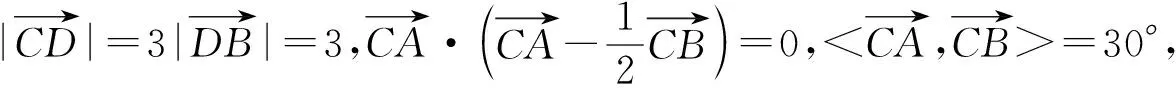
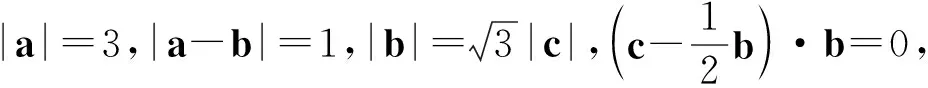
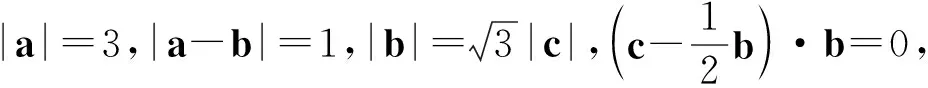
问题8(延伸问题4).

练习1已知向量a,b满足|a|=1,=60°且c=-2a+tb(其中t∈R),则|c|+|c-a|的最小值______.

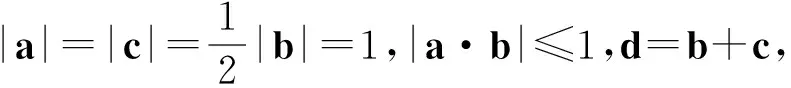
问题9(提炼问题2)以向量的共线问题为例，使向量语言与几何语言实现相互切换.

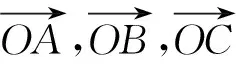
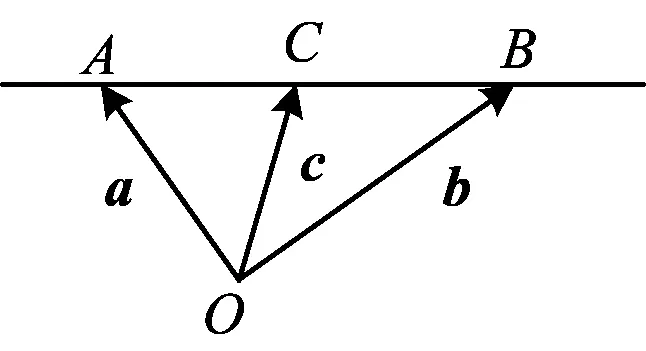
图10

课堂预设平面向量中引入参数，激活了图形的变化.在动态几何中，恰当的“文式图”的建构是图形语言和向量条件间切换的“密码”，从而实现了代数与几何间的自由切换.

课堂生成以常见几何元素的“文式图”为例，以小组为单位，拓展思维，展开丰富的几何元素与向量语言的转换的拓展性作业，以思维导图呈现.

课后练习请设计一张平面向量中常见向量语言与几何语言问题清单.

3 结语

结构化是数学问题中的一个典型特征——数学对象之间存在着各式各样的联系.本文以平面向量的解题项目化教学为例，给出了基于提升学生数学学习力的解题教学原则与问题链的设计策略.课堂的主干问题链设计，立足基本知识，突出核心思想方法——向量代数与几何的自由切换.表现在：一方面，通过课堂预设与课堂生成，将课堂在教师的导引下以学生为主体，强调在思考的脉络中不断延伸和拓展问题，以此激发学生探究数学知识的思维，提升数学学习力.另一方面，通过提炼问题，引导学生参与和归纳解题思想方法，给出思维导图式的解题策略和文式图表示的知识清单，真正落实核心素养下的解题教学目标.