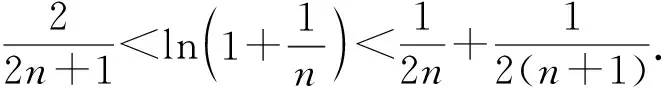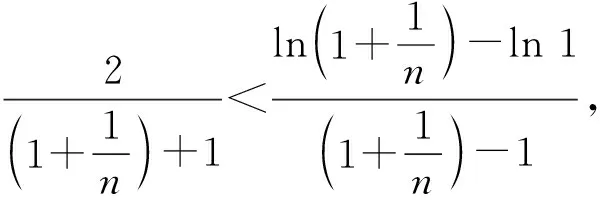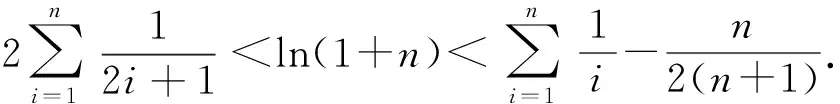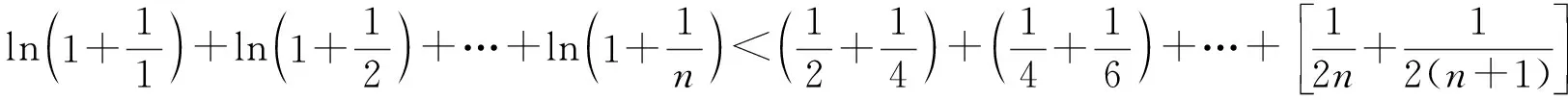高观点下对数均值不等式的证明及推广
吴俊凯
(义乌中学,浙江 义乌 322000)
近些年,全国各地的高考卷中含ex,lnx的函数零点、方程的根、极值点偏移及数列中的不等式的相关问题成为考查的热点,常出现在各地模拟卷及高考卷压轴题中.“对数均值不等式”是解决此类问题的一个简化工具,其价值也不言而喻.以下不等式的证明将结合初等方法和高观点的证明方法来加深学生对该不等式的理解与应用.
1 对数均值不等式
两个正数a和b的对数平均定义如下:
2 对数均值不等式的证明方法
该不等式的证明有多种方法,下面笔者整合了3种初等的方法和6种高观点下的证明方法.
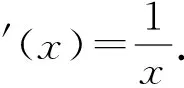
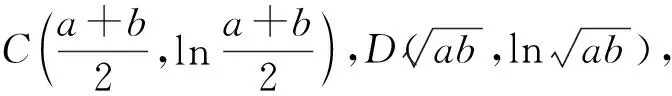
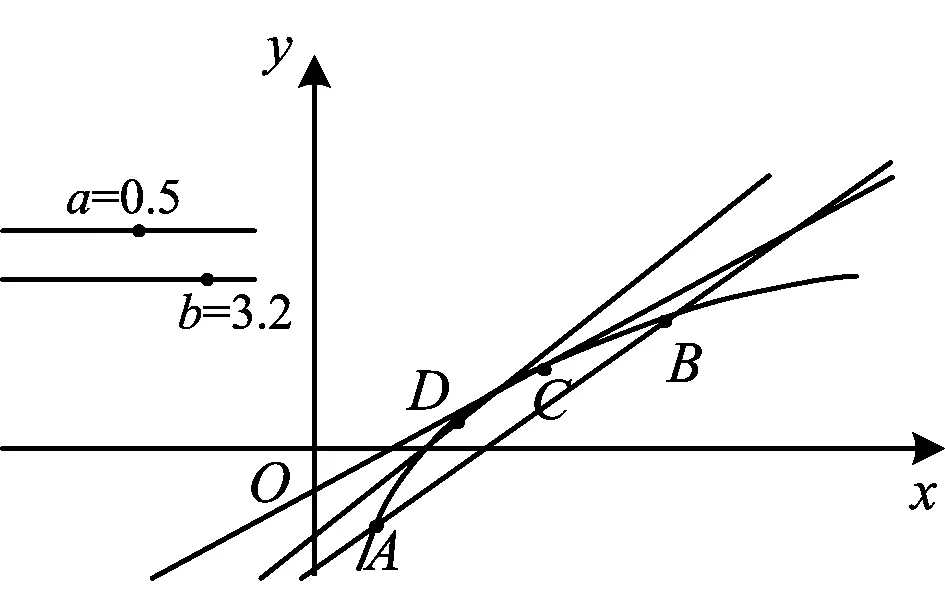
图1
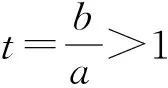
移项构造函数求导求最值可证.
证法3[2](主元法)设b>a,则
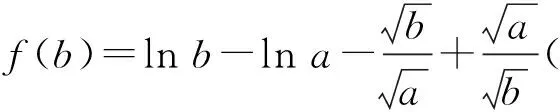
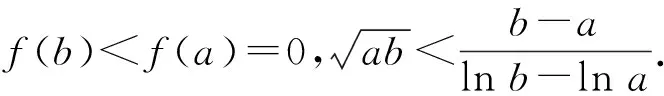
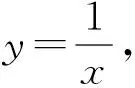
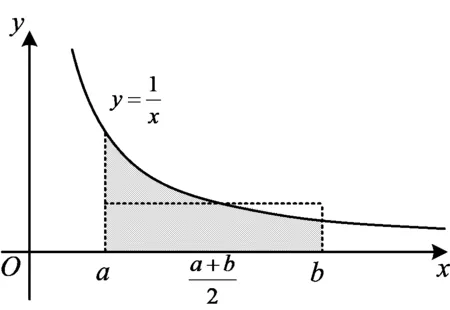
图2
因为S矩形 图3 由S阴影 于是 证法7(拉格朗日中值定理法)构造f(x)=(x+a)(lnx-lna)-2(x-a)(其中x∈[a,+∞)),从而 根据拉格朗日中值定理,存在ξ∈(a,x),使得 可得f(x)在[a,+∞)上单调递增.因此令x=b>a,则 同理,构造 于是g(x)在[a,+∞)上单调递减.因此令x=b>a,则 同理,存在ζ∈(1,x),使得 由柯西不等式,可得 又由幂平均不等式,可得 对数均值不等式是双变量不等式,直接证明具有一定的难度.给出的后6种证明方法结合了高等数学中的定积分、积分形式下柯西不等式、拉格朗日中值定理、柯西中值定理、函数的级数展开和幂平均不等式等知识.高中生提早接触高等数学的知识,可以帮助他们用高观点去思考和解决数学问题,有助于他们认知的提升和思维方式的训练. 得证. 证明由推广1可得 得证. 推广2可以应用于真数为正整数的对数的估计,也可应用于离散型级数求和的估计[3]. 对数均值不等式的证明方法灵活,形式也多样,以上展示的证明方法具有一定的典型性.对数不等式不仅可以进行拓展延伸得到许多不等式结果,也可以应用于例如极值点偏移等一系列问题,因此对该不等式的研究是有意义和价值的.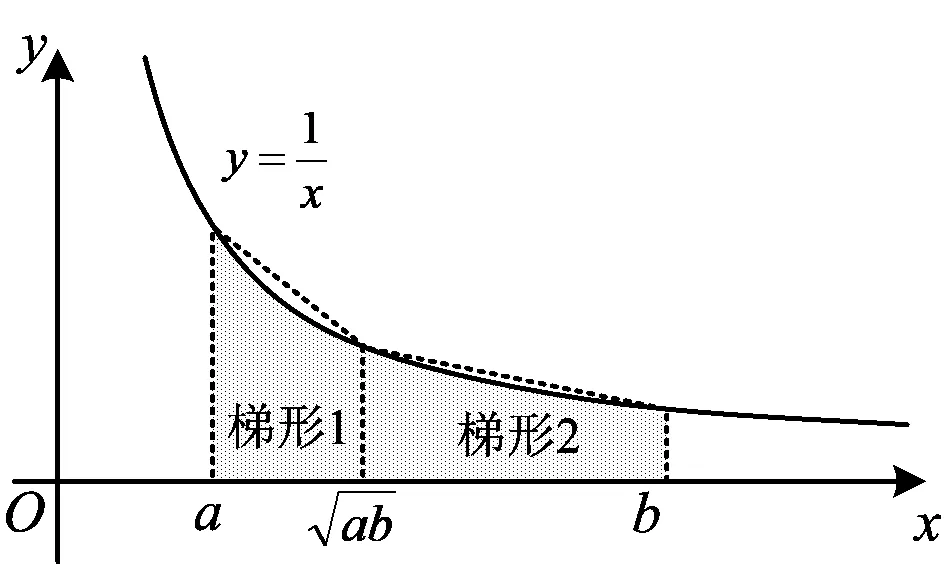
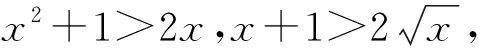
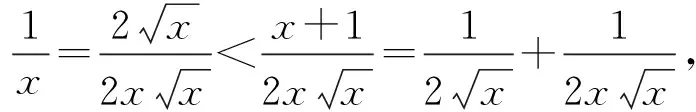
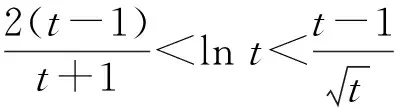
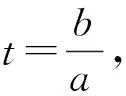
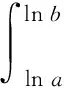
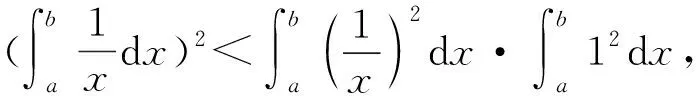
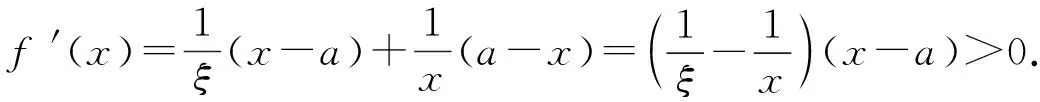
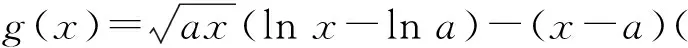
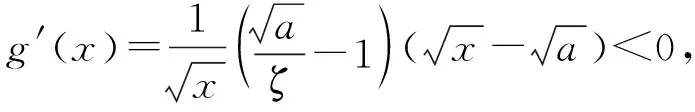
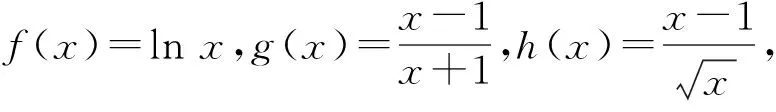
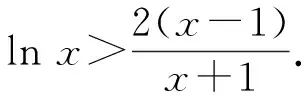
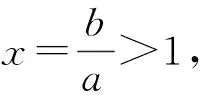
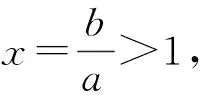
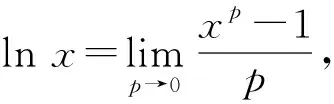
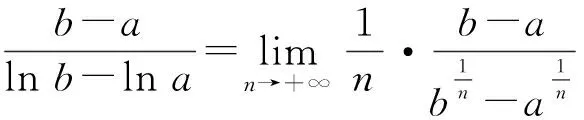
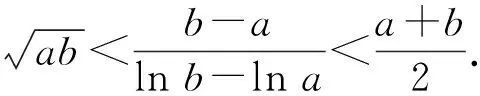
3 对数均值不等式的推广