深化问题理解 强化问题探究 提升数学素养
郑 良
(合肥市第四中学,安徽 合肥 230000)
1 问题提出
在实际教学中,教师往往要面对不同课型的教学,如新授课、复习课、习题课和试卷讲评课等.复习课又可分为单元复习课、整章复习课和模块复习课.每种课型都有着各自不同的特点和功能定位,只有抓住了各种课型的功能定位,才能上好不同的课型,才能使得每一种课堂都比较有效[1].新授课要关注知识的生成和知识的运用,知识的学习主要是由薄到厚零散积累的过程.复习课要关注知识的梳理和知识的综合,知识的系统化主要是由厚到薄的过程.研究表明:一个能够解决问题的“专家”,具有内容丰富、联系紧密、区分明显、有层次的知识结构[2].高三第二轮复习课不同于新授课,也不同于第一轮、第三轮复习课.高三第二轮复习课到底怎么上?最近笔者随堂听了教师A执教的一节题为“圆锥曲线中的最值、范围问题”的高三第二轮复习课.下面笔者选取一道例题,简要呈现教学过程,剖析学生在解题中的疑难困惑,结合教学实践给出思考与建议.
2 教学过程呈现
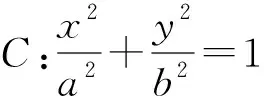
1)求椭圆C的方程.
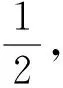
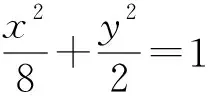
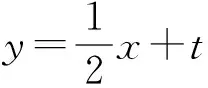
x2+2tx+2t2-4=0.
由Δ=16-4t2>0,得
-2 设点P(x1,y1),Q(x2,y2)(下同),则 x1+x2=-2t,x1x2=2t2-4. 由点P与点E关于原点对称知点E(-x1,-y1),从而 (2-x1)(y2-1)-(2+x2)(y1+1)=2(y2-y1)-(x1y2+x2y1)+x1-x2-4 =x2-x1-(x1x2+tx1+tx2)+x1-x2-4=-x1x2-t(x1+x2)-4=0, 对于第2)小题,教师A呈现的解答(参考答案)犹如“天外来物”,学生都表示“听得懂,想不到,学不会”.教师A没有说明如何发现kAE+kAQ=0,没有对接学生的想法,自然无法解决学生的困惑,如此学生下次遇到类似问题依然困难多多,束手无策.教学的基本要求就要让学生“想得起,弄得清,用得到”,基于此,笔者对上述教学进行了改进. 教师先展示参考答案,引发学生的困惑,让学生在充满困惑和兴趣中整装待发. 师:对于第2)小题,已知条件有哪些?这些条件如何表示?求解的目标是什么? 当且仅当点Q与点E重合于(2,1)、点P的坐标为(-2,-1)时等号成立. 生1的分析与教师的补充结合即为完整的解答,记为证法2.接着,生2给出了证法3: 师:证法2与证法3的区别与联系在哪里? 生3:它们均为基本量法,证法3直接用t表示点P,Q,E的坐标,证法2先(局部直接或间接)利用一元二次方程根与系数的关系,再代入进行证明,强调了整体运用. 即 亦即 cosβ=-sinα, sinβ=-cosα, 师:证法2与证法4均构建函数,本质是消元法.证法1借助对称关系确定kAE=-kAQ,均将非对称问题“转化”为对称问题,体现了化归与转化思想.请同学们比较证法1与证法2~4,交流一下你们的想法. 小组内研讨,不同组间交流. (1+4k2)x2+8kmx+4m2-8=0, 由Δ=16(4-m2)≥0,得 -2≤m≤2. 而当m=-2时,点E与点Q重合于点(-2,-1),kAE,kAQ均不存在,从而m∈(-2,0)∪(0,2],于是 当且仅当m=2时等号成立,此时点E与点Q重合于点(2,1). 师:生6的分析非常精彩,深化了我们对解析几何中对称问题和非对称问题的理解,给出了证法1的合理性. 师:同学们能对本题进行改编吗? 学生尝试改编例1,其中以下变式1的形式最多. 1)求椭圆C的方程. 师:若以该变式为母题搭建台阶,则例1的难度能有效降低. 师:请同学们仔细审题,提出你的想法? 学生经过探究,得到如下一般性结论: (a2k2+b2)x2+2a2kmx+a2m2-a2b2=0. 师:请同学们课下思考各种证法的原理与本质,并尝试探究更多的结论. 当前教学中“重技巧、轻知识”“重套路(现象)、轻本质”的情况较为普遍.对于相同或类似的问题,学生尝试浅层次“对号入座”,遭遇挫折就基本宣告失败.“对号入座”的“号”就是数学活动经验中积累的数学模型,只有对该模型深入理解,遇到问题才有可能灵活运用.夯实“四基”是教与学的基本要求,提高“四能”是教与学的目标要求.“缺乏‘四基’,空谈‘四能’”便会遭遇无源之水,无本之木.在教与学中,我们要力争“知其然,知其所以然,知其何以所以然”.只有切实理解知识的功能与作用,才能物尽其用. 李大潜院士说:“一个人要做学问,要做得好,最重要的就是坚持,五分钟热度不行,要一辈子坚持.”人的认知具有层次性,均是从肤浅逐步走向深入.具有普适性的“笨”方法思路易得,结果难求.学生要多经历、体会与感悟问题的生成与发展的曲折过程,提高运算求解等数学核心素养.在不断磨砺中反思出现困难的原因,寻求方法上的突破,进而搭建整体结构,规避局部对象的求解,实施整体代入,优化解题过程.如本文例1中诸多条件的使用,本质就是交集思想方法的理解与应用. 无论是新授课与复习课,它们共同的目的都是为了建构良好的知识结构,建构过程中的不同阶段会表现出不同的学习水平.新授课通常是学习新知识,具有丰富的事实性知识、方法性知识,或者如现象、概念、规律、模型等学习内容.复习课通常是为优化知识结构而进行的学习.知识结构在转化过程中会产生一些新的知识,如方法、策略、联系性知识、区分性知识、抽象性知识.与新授课主要关注知识内容不同,复习课的教学目标既要关注结构变化,又要关注新内容[2]. 一些教师为保证完成任务往往采用自我可控的讲授法较多,压缩了学生自主参与体验活动的时间[4].由于每年的高考、模考试题都会产生大量的“新题”“好题”,导致教师在选题时“爱不释手”“不忍割爱”.数量越来越多,无形之中形成的“题海”必然导致教学中囫囵吞枣、浅尝辄止,教学只重视答案的获取,不顾学生的认知与感悟,造成了学生的“被动”接受,长此下去,学生失去数学学习的兴趣,甚至产生数学“恐惧症”和“厌恶感”[5].教育归根结底是通过行动培养学生良好的学习与生活习惯,形成良好的思维品质.对于教学,不仅仅是教师要明确教学目标,稳步推进与实施,还要让学生对教师的课堂结构具有清晰的认知,明确学习目标与任务. 新授课内容相对简单,有较多的资源可供参考,如与教材配套的教师用书等,而复习课可供参考的资源不多,往往只是知识点与题型的简单累积.学生对复习课的内容相对熟悉,教师有效地激发学生的学习兴趣离不开对课堂教学的精心设计.如教师要思考选择例题的目的是什么,该例题是否必要,可有更典型的例题进行替代,如何构建变式题组,各个例题之间具有怎样的关系,课堂教学的主题是否明确,主线是否清晰.复习课也要有适度的情境,抓住逻辑与结构,注意问题之间的衔接与过渡,让学生弄清问题的来龙去脉.如证法1的“首先展示”比“最后呈现”更能激发学生学习的兴趣.对于每一类问题,通过几道题将其研究得通透要花费一定的时间与精力,但它比浅尝辄止地做更多题在总体的时间花费、思维的有序化与调整策略、解题的过程优化等方面受益会更多.如教师可引领学生思考“本题为什么出现非对称”,即培养学生探究方法和理性精神.教师自己心里要清楚,学生的数学学习不是教师讲明白的,而是学生自己想明白的.要培养学生的数学思维,一定要留有时间让学生去思考.数学教学要不求快,而求深[3].如案例中提供的改编试题质量并不高,学生探究的结论也较为明显.但学生通过它们可以了解例题的演变过程,强化探究问题背景的意识与习惯. 雅思贝尔斯认为:对学生来说,仅仅获得知识是不够的,他们还应成为完整的人,因此需要的是全人教育.现在的教师就是过去学生的延续,而在一定意义上,现在的教师也是学生将来的模样[3].教师教学的照本宣科,实质是其教师素养难以支撑起课堂教学的体现.学生的全面发展离不开教师的全面发展,那么教师如何提高自己的素养呢?笔者认为教师可通过持续地广泛涉猎、静心思考、勇于实践、反思提炼等行动保持终身的学习能力.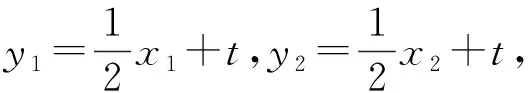
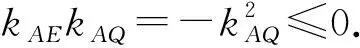
3 改进教学
3.1 探寻不同的证法
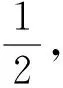
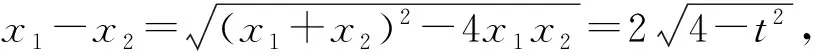
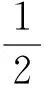
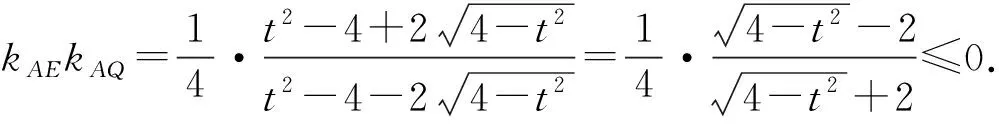
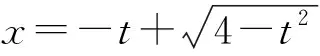
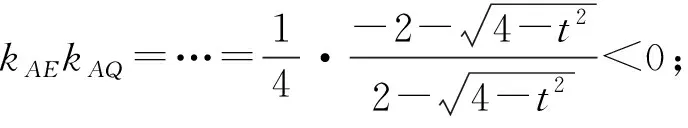
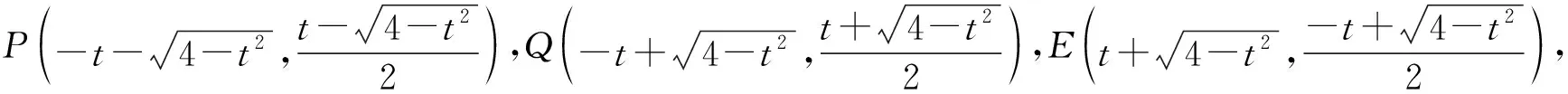
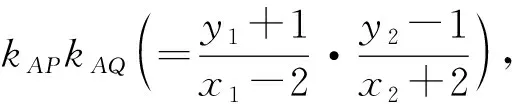
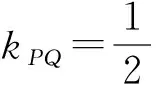
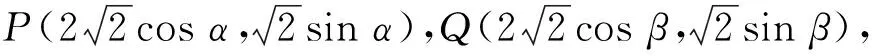
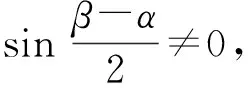
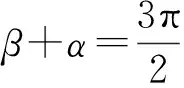
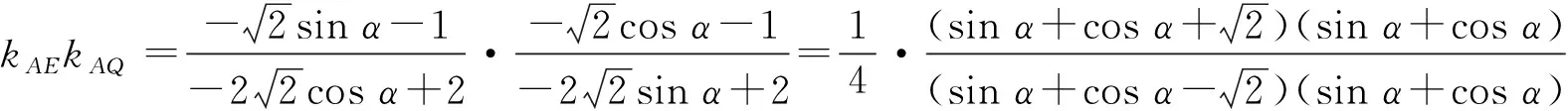
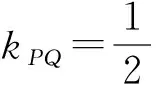
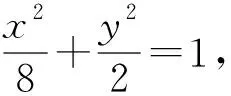
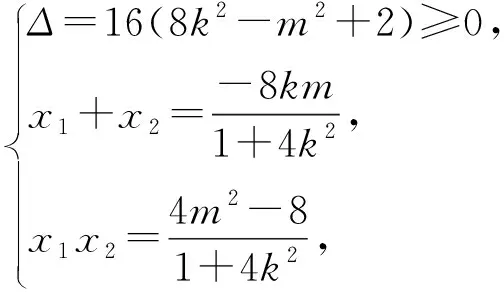
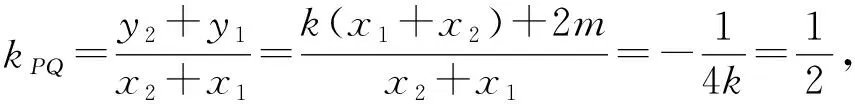
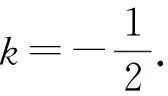
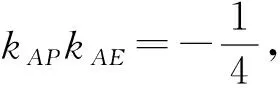
3.2 改变问题形式
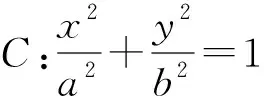
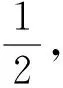
3.3 推广一般结论
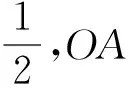
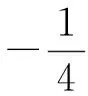
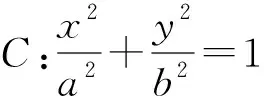
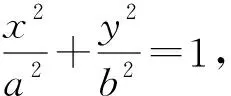
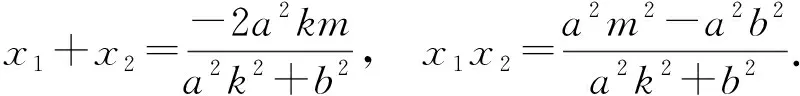
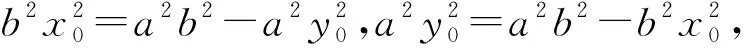
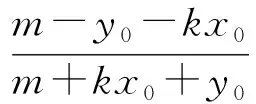
4 思考与建议
4.1 强化内容理解,构建整体结构
4.2 明确功能定位,对接学生认知
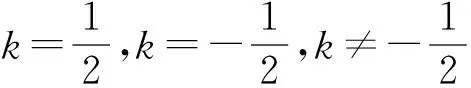
4.3 聚焦当前任务,明确长远目标
4.4 强化终身学习,提升教师素养

