“评、学、教”一体化视域下的数学课堂及思考——以“三点共线”复习课为例

刘清清， 赵玉斌， 卫德彬, 陈方勇

(1.上派初级中学，安徽 肥西 231200；2.合肥市第四十六中南校区，安徽 合肥 230092)

0 引言

复习课首先要帮助学生复习已学知识，完成查漏补缺，实现巩固提升.通过背诵、默写、罗列等方式简单再现概念、公式、定理、法则等基本知识，是“炒冷饭”，不利于学生的理解提升[1].让教师感到无措的是：学生对复习课失去了探究的热情与欲望，参与课堂的积极性和主动性不高，导致教师不能正常评估学情，不能准确地进行形成性评价.因此，初中数学复习课是困扰教师教学实践的难题之一.“评、学、教”一体化的理念是将教学评价前置，根据评价及时组织教学,而复习课恰恰缺失实时的教学评价.“评、学、教”一体化可以从另一个视角对知识进行再认识，并使复习的知识再结构与重组.本文以“三点共线”复习课为例，具体铺展“评、学、教”一体化的教学.

1 “评、学、教”一体化的数学复习课

本环节将分为3个部分拆解“评、学、教”一体化在数学复习课中的实施和应用.

1.1 以“疑”引“评”

课堂伊始，教师与学生互动交流，展示例题.

例1如图1所示，网格中有甲、乙、丙、丁4个图形，经过旋转或平移变换后形成图2，图1中的图形面积是64，图2中的图形面积是65，根据该变换，得到64=65.那么64=65吗？

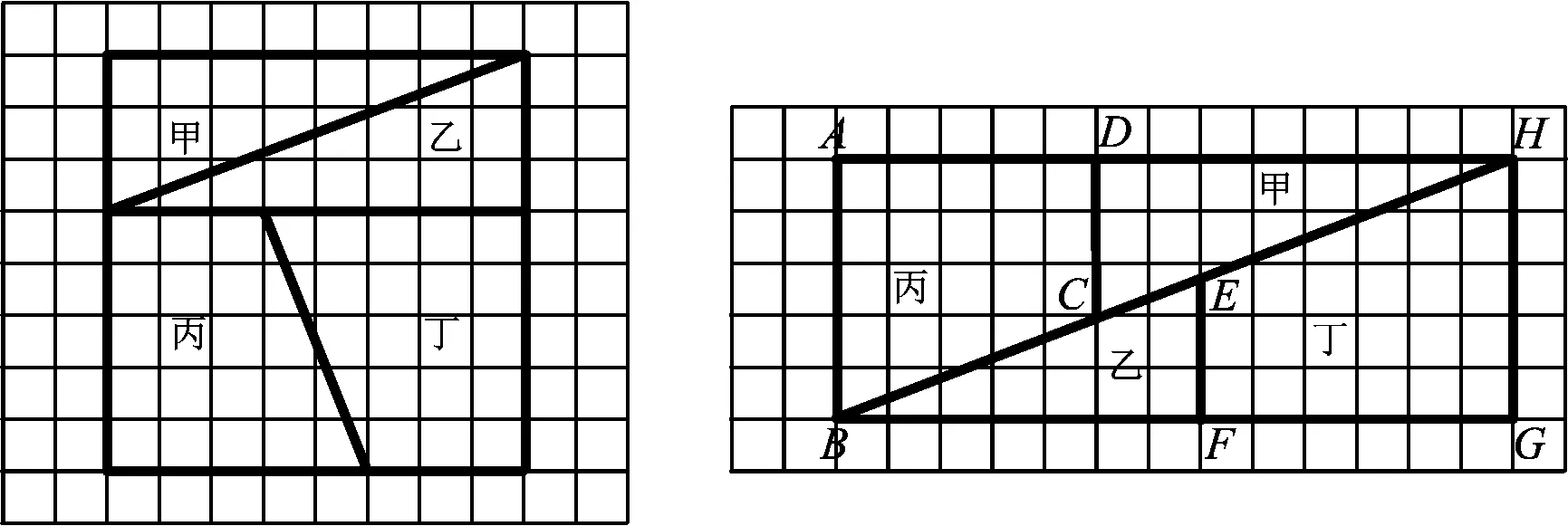
图1 图2

设计意图“评、学、教”一体化教学理念下的复习课，需要教师聚焦特定的学习主题，使用适合的资源，选择匹配的学习指导方法，才能达成教学目标.若是直白抛出复习主题“三点共线”，则难免又陷入“复习知识点→讲解→巩固练习”的老路.因此在确定了复习主题后，教师选择了一道富有数学趣味的例题.所有的学生对例1均有所思，在质疑的过程中教师能够积极调动学生头脑中已有的知识经验，让每一位学生均有所获.这与《普通高中数学课程标准(2017年版)》中的理念“面向全体学生”相吻合.以“起点低、反常理、思路广”的方式引起学生的注意，引发学生积极思考，为下一步形成性评价做好铺垫.

1.2 以“评”牵“学”

例题的呈现让学生先是质疑、接着困惑、最后跃跃欲“算”，转折起伏的心理活动展露了内在知识的筛选过程和思维的流动.学生对疑惑的解释亦是可爱.

师：以上的问题出现在哪里呢？

生1：我认为问题出现在“对角线BH”上，中间应该是有缝隙的，导致了面积增加.

师：如何从数学角度刻画这条缝隙，可以通过怎样的数学方法来说明？

生2(直角三角形的方法)：根据勾股定理可知

显然

即

BC+CH≠BH，

说明点B,C,H不在同一条直线上.同理

显然

即

BE+EH≠BH，

说明点B,E,H不共线，进而说明了“缝隙”的存在.因此拼接之后的图形与原来的不相等.

生3(相似三角形)：假设点B,C,H共线，则

△HDC∽△HAB，

从而

∠DCH=∠ABC.

根据图2可知

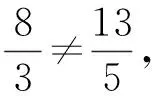
点B,E,H不共线，也能说明图2存在“缝隙”.

设计意图在本环节上，教师没有破解谜题，而是用“问题出现在哪”来回应学生的质疑.虽然学生用生活化的语言描述了数学问题的原因，但这并不影响学生对问题的分析，反而是认知“三点共线”更直白、更易于理解的描述方式.教师用“刻画缝隙”“数学方法”牵引学生从语言描述走向数学说理，从感性质疑到理性印证，顺水推舟般让学生自主学、自主思、自主做.教师通过“数学角度”“多种方法”等形成性的评价语言鼓励、引导学生积极思考.同时，学生需要将现实生活中的“缝隙”转化为数学中“三点共线”的知识，这一转化亟需学生调动数学抽象思维，转化为数学图形，进而实现从数学问题到生活表述再到数学探究的华丽转身.

1.3 以“学”推“教”

师：以上同学们运用了哪些知识破解谜团？在什么情况下，能够运用这些知识解决问题？

生4：在直角三角形中，想到了勾股定理和解直角三角形；由线平行联想到角的数量关系和三角形相似.

师：以上同学们回顾的知识都属于“图形与几何”的模块，也就是说从“几何”的角度可以解决“三点共线”的问题，还有其他的角度可以说明三点共线吗？网格在学习什么知识时高频出现？

生5：平面直角坐标系.

师：该例题如何在平面直角坐标系中说明三点共线呢？

生6：以点B为坐标原点、以BA为y轴、BG为x轴建立平面直角坐标系.由B(0,0)，E(8,3)确定的直线方程为

当x=13时，

设计意图由于图形的特殊性，生2和生3的证明方法较易得到，但是利用函数思想判断三点共线对学生来说是困难的，甚至“难以想象”，因此这里需要教师引导与提醒.教师由“网格”引导联想到“平面直角坐标系”，再联想到“判断点是否在直线上”.整个联想的过程需要学生积极构建平面直角坐标系与点坐标之间的联系，再联想到直线方程(一次函数).本环节，由学生的已学方法拓展到待学方法，需要教师的引导与启发，从“学”推动“教”，在鼓励学生动脑动手的过程中收获了新知.

1.4 以“教”再“评”

课堂总结是对知识网络再建设性地构建过程，“评、学、教”的课堂亦是如此.在完成“评、学、教”之后，学生跟随教师一起构建如下的知识结构图，对本节课再进行整体评价.微观上展示三点共线的不同方法，宏观上展示解决问题的不同视角，拓宽学生的认知地图.特别说明的是，在初中阶段，学生对向量和斜率是陌生的，因此教师只需点到为止，将解决问题的触角延伸到高中阶段，为即将到来的高中学习增添熟悉感.

2 教学思考

在传统的“教、学、评”设计中，“完整地”完成教学内容是教师的关注重点，课堂绝大部分时间是教师讲授，教师将重点内容讲授结束后才是学习效果的评价或测试，或者将评价重点安排在教学过程外的测验和考试，课堂上对“评价”的部分进行时间上的挤压与空间上的外置.而“评、学、教”一体化将颠覆传统设计，结合本文案例，笔者做几点反思.

2.1 对“评”的反思

“评、学、教”一体化可以简单地理解为现有的教学评设计模式的逆向教学设计，是对常规教学思维进行的逆向思考.而这种逆向的思考有着教学的现实诉求.“教、学、评”模式将对学生的评价置于课尾或课下，这无形之中将学生的渐进式成长推出了教师的引导之外，让教师不能正确地、精准地把握学生的实际学情.而“评、学、教”一体化首先将“评”置于首位，评价优先于教学活动，在确定了教学目标之后，设计达到预期目标的评价任务(学生有什么表现)，再基于评价任务组织相应的学习活动(活动的组织有针对性).笔者认为：在“评”的环节中，应该包含评知识内容、评数学方法、评知识结构这3个维度，才能较全面地评价学生当前的学情与认知生态.在本案例中，教师的最终目的是得到图3，但是教师在组织教学之前并不清楚学生对图3的认知程度，因此在教学之初，以趣味数学题引入，接着教师用“问题出现在哪”“用数学的方法如何刻画”等评估学生对三点共线的认知程度，并根据学生的回答(“缝隙”)再组织学生进行教学学习.另外，笔者认为“评”不仅体现在教学之前，还应该在课程之尾再次对学生进行评价，由此形成“评、学、教、评”的闭环，首尾相接，环节之间彼此互动与衔接.

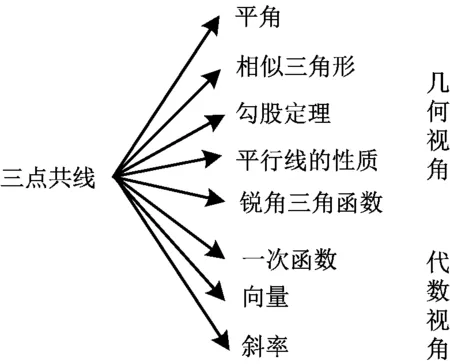
图3

2.2 对“学”的反思

无论是“评、学、教”一体化还是“教、学、评”一体化，最终的目的就是让学生“学”与“做”，而“评、学、教”一体化的“学”又有不同.“评、学、教”一体化的评价不仅先于教学活动设计，而且教学全程指向学生的学习成果.从最开始的评价任务到学生利用数学方法说理“缝隙”的存在，均是指向学习成果(图3).而学生的“学”应该是教学评价的驱动下做出的思考动作.笔者认为“评、学、教”一体化中的“学”应该包含多个层面，如自主地学、合作地学、教师引导地学或自我反思总结.也就是说，“学”不应该仅仅局限于评价之后的学，不管处于哪个环节，在课堂中都要组织各种教学形式促进“学”，而促进“学”的最佳助攻就是合情合理的教学评价.

2.3 对“教”的反思

在“教、学、评”模式中，把“教”放在首位，课程的教学活动均是围绕着教学目标展开教学，而教学活动的执行者与策划者是教师.教师为了达成教学目标，首先进行教学活动.但是教学活动的基础和前提是学生的认知基础.在“教、学、评”的模式下，学生的认知基础是上一节或上一阶段的教学目标，实际上这已经偏离学生的实时学情，因此虽有教学目标作为参考，但在组织教学活动时缺乏具体评价任务的指导，学生的学习得不到及时监测，活动形式的选择也不是那么贴切与匹配，因而导致缺失教学评价或进行无意识、不明确的教学评价任务，整节课就会“面面俱到，博而不精”.与之相反的“评、学、教”一体化的教学模式却将教学放在了尾部，这并不意味着淡化教师的“教”，反而是强调了“教”，更注重“因何而教”“为何而教”“因势利导”.在这种理念下，教师仍然依据教学目标进行教学活动，是依据对学生评价后而进行的有目的的教学.透过对学生的评价探得学生的认知结构，进而调整教学活动与任务，更好地实现教学目标.在“评、学、教”一体化的模式下，因为以评价为导向使得教学中的目标评价更加清晰、具体、明确、可测评，所以能够更好地紧扣目标，实现“一课必得”.

“评、学、教”一体化遵循“教学目标—评价任务—学习活动”的线路，逆向设计坚持目标倒逼、效果倒追的原则，让评价前置，诊断和促进教学效果.教学目标的重要性是贯穿整个设计的，后续的教学设计都要以目标作为中心指导，教学则是为了帮助学生达到学习目标的一个过程.由此可见，“评、学、教”一体化的教学模式在初中数学复习课中已较好地实现了价值，着实值得继续探索与尝试.