三角矩阵环上FC-投射模的刻画

吴德军, 付家慧

(兰州理工大学 理学院, 甘肃 兰州 730050)

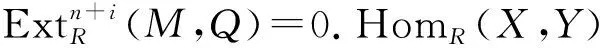
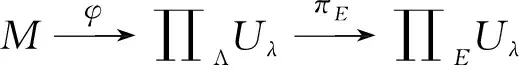
定义2[6]称左R-模M为有限余表示模,如果左R-模M是有限余生成左R-模,并且对于任意的正合列0→M→L→N→0,若L是有限余生成模,则N是有限余生成模.

引理1[6]设0→M1→M2→M3→0是左R-模正合列.

1) 如果M1和M3是有限余表示左R-模,那么M2是有限余表示左R-模.

2) 左R-模的有限直和是有限余表示模当且仅当任意的直和项是有限余表示左R-模.

引理2[7]环R是左余诺特环当且仅当任意的有限余生成左R-模是有限余表示模.

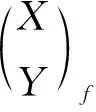
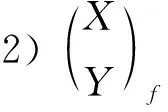
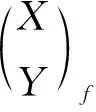
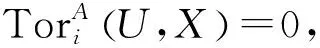
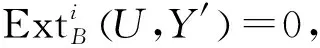
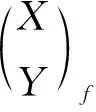
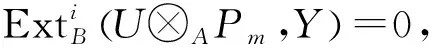
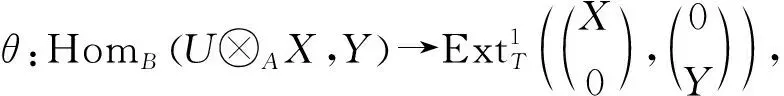
进而由伴随同构知：

HomB(U⊗AX,Y)≅HomA(X,HomB(U,Y))

2)i=0时,由1)可知.下证：i≥1时成立.存在正合列:

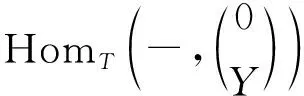
得到

又由引理4可知：

进而得到

3)n=0时,由1)可知.下证：n≥1时成立.对X作投射分解有左A-模正合列：

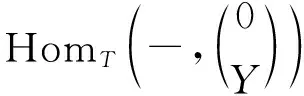
…→HomA(Pm,HomB(U,Y))→

HomA(Cokerdm+1,HomB(U,Y))→

因为Pm为投射左A-模,所以

由1)知：

HomA(Cokerdm+1,HomB(U,Y))

进而得到以下交换图1.

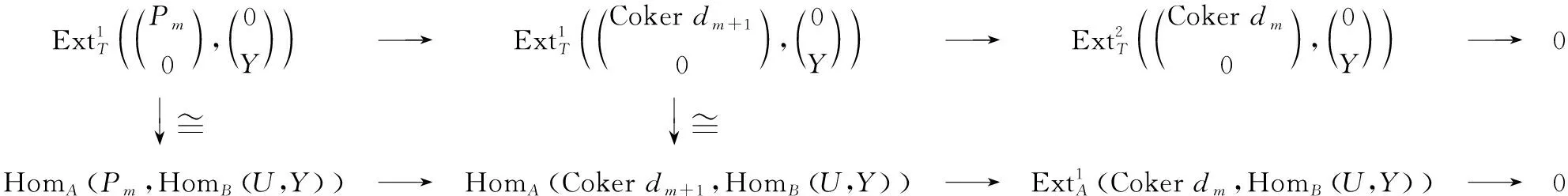
图1 交换图

由引理5可知：

进而有

所以n=1时成立.

当n≥2时,有长正合列：

由2)和假设可知：

所以有

进而有

由维数转移可知：

因为n=1时已证得成立,所以有

又由维数转移可知：

进而得到了同构式：

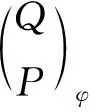
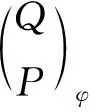
又因为

直积函子是加法函子,所以有

进而有左T-模正合列：

进而有左B-模正合列：

从而Q,P为有限余生成模.

如果Q为有限余生成左A-模,P为有限余生成左B-模,那么由定义1知对任意的单同态Q→∏ΛUλ,P→∏Λ′Vλ′存在正合列：

0→Q→∏ΛUλ→∏EUλ→0
0→P→∏Λ′Vλ′→∏E′Vλ′→0

从而有左T-模正合列：

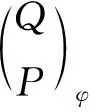
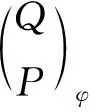
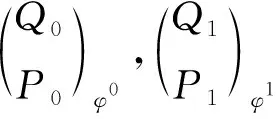
证明因为AQ是有限余表示左A-模,所以存在正合列：0→Q→Q0→Q1,其中Q0,Q1是有限余生成内射模.进而存在左T-模正合列：

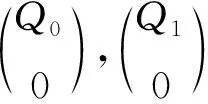
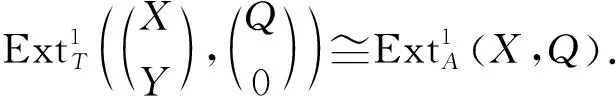
对于任意的有限余表示左B-模BP,由引理4有

下证.

0→HomB(U,P)→HomB(U,P0)→HomB(U,P1)

进而有正合列：

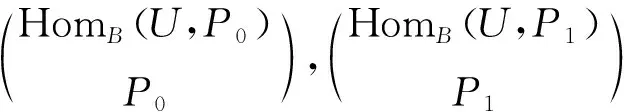
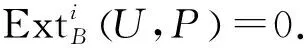
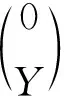
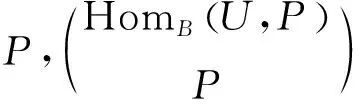
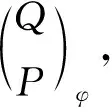
进而有

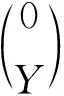
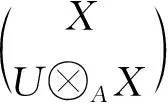
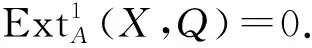
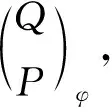
由引理4知：

又因为A为左余诺特环,X是FC-投射左A-模,根据引理2可知Q是有限余表示左A-模,所以

进而有

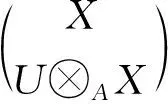
由引理5有

又由引理4有

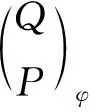
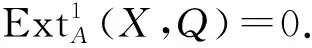
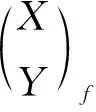
定理2考虑以下条件：

2)X是FC-投射左A-模,Cokerf是FC-投射左B-模且f是单同态.

故X是FC-投射左A-模.下证：f是单态射.

对于有限余表示左B-模BW,存在正合列：

所以上正合列右正合得到满同态g:

又因为

HomA(X,HomB(U,W))

HomA(X,HomB(U,W))≅HomB(U⊗AX,W)

所以有交换图2.

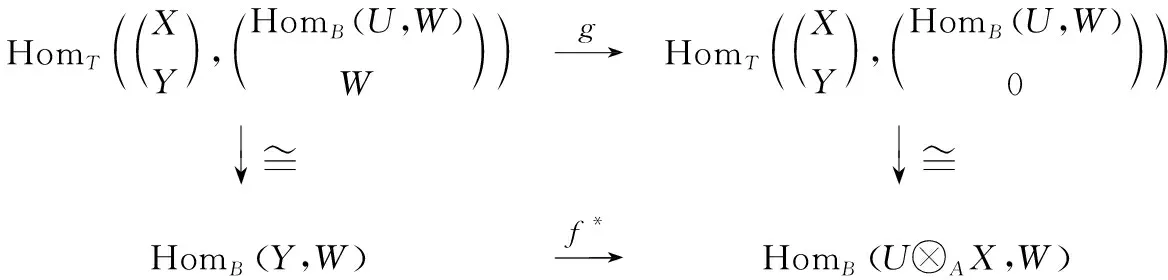
图2 交换图

进而有f*是满同态.因为BW为内射余生成子,所以f是单同态.下证：Cokerf是FC-投射左B-模.

因为f是单同态,所以存在正合列：

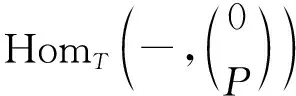
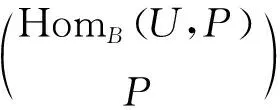
又因为

所以

进而有Cokerf是FC-投射左B-模.

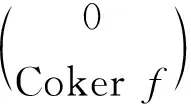
命题4设A为左余诺特环,AU是有限表示左A-模.如果满足以下条件：

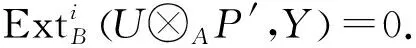
2) FC-pd(BB)≤n-1,FC-pd(AA)≤n,FC-pd(BU)≤n-1.

那么有FC-pd(TT)≤n-1.

其中i≥2.因为AU是有限表示左A-模,根据文献[6,30.5]有HomB(U,P)是有限余表示左A-模,所以有

其中i≥1.进而有

其中i≥2.

因为FC-pd(BU)≤n-1,所以

其中i≥2.进而有

其中i≥2.又因为FC-pd(BB)≤n-1,所以

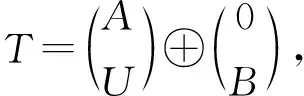
其中i≥2.从而有FC-pd(TT)≤n-1.

由命题4可得

FC-pd(T2T2)≤n-1.