在初中几何教学中渗透维数知识的几点思考
卢敬棣
[摘 要]维数是中学数学教学中时常用到的概念,但目前中学数学教材内容几乎没提到几何图形的维数概念,因此有必要渗透维数知识教学。人们认识维数经历了一个复杂的过程,在初中教学中渗透维数知识是有意义的和可行的。但在教学中不宜喧宾夺主。
[关键词]数学教学 维数 几何图形
新课程要求教师不仅仅是课程的实施者,还应该是课程研究、课程建设、课程资源的开发者。具有多重角色的数学教师要根据学生的认知水平和原有的知识、活动经验,灵活结合教学内容,设计出合适的教学素材,以使数学新课程有利于学生的发展。维数是几何图形的一个性质。凡学过数学的人,对某些几何图形的维数总以为是了解的,如“直线是一维的”、“抛物线、圆是二维的”、“长方体、四面体是三维的”。但细究一下,许多问题又模糊起来。例如:“直线是一维的”,为什么?几何图形的维数是怎样规定的?几何图形的维数只是整数吗?这些问题的回答是有点难度的,需要现代数学的知识来解释。几何图形的维数具有既简单又复杂的双重身份,是教师在初中几何教学中值得开发的资源,有利于开阔学生的数学视野。
一、人们认识维数的历程
简单地说,维数就是刻画几何图形性质的数,但人们对它的认识,却经历了一个不断深化的过程。以往,人们从图形中的点的位置的确定需要几个独立参数的观点,认为直线、线段和曲线是一维的,因为其上的点依赖一个参数s=s(t);平面和平面区域是二维的,决定其上一点需要两个参数(二度坐标);现实空间和立体是三维的,需要三个参数(三度坐标)才能决定其上一个点的位置。
在康托尔揭示了线段上的点集与空间的点集的等势性以后,皮亚诺建立了线段到正方形的连续映射,数学家们于是开始明白,图形维数这个直观明显的概念需要精确的叙述,应用边界的概念,这个概念可用下列方法来形成:空集有维数-1;如果集合X的任一点具有这样的任意小邻域,其边界的维数为n-1,则集X的维数为n。例如,孤立点的维数是0,因为它的邻域是空集且维数为-1,由n-1=-1得到n=o,所以得到孤立点的维数是0;而直线的维数为1,因为直线上任一点有任意的领域,其边界由两点组成且是零维的,由n-1=0得到n=1,所以直线是一维的;类似地可以得到圆域是二维的,球体是三维的。拓扑空间的维数是拓扑性质,即在同胚映射下是保持不变的。可以证明,在中学数学中研究的任意曲线(圆、双曲线、抛物线、函数图象等)的维数等于1,任意曲面的维数等于2,球以及其他空间立体的维数等于3。
二、在初中几何教学中渗透维数知识的意义
1.扩大学生的数学文化视野。数学新课程提倡在教学中注意渗透数学文化知识,扩大学生的数学文化视野,以激发学生的学习兴趣,提高学生对数学的整体认识,提高学生的数学素养。维数在几何教学中偶尔被提到,但目前初中数学教材几乎没有维数的一席之地,目前没有哪个版本的初中数学教材涉及到维数的内容,所以对这个在几何教学中偶尔遇到的概念,在提倡数学文化教育的新课程背景下,我们在教学中是有必要渗透的。维数概念经历了由初等数学的明显直观性到现代数学的精确叙述性,是“人类对数学的认识是一个不断发展的过程”的一个体现,是“数学是系统的、严密的”一个体现,是“数学崇尚理性”的一个体现。
2.促进学生形成正确的维数观。为了了解学生对几何图形维数的认识情况,笔者设计了一个调查问卷,对本校初一的40名学生进行了调查,具体内容主要涉及三个维度:判断一些常见几何图形的维数;获得几何图形的维数的途径;倾向学习维数知识的主观意愿程度。在第一维度调查中,学生能正确判断一些常见图形的维数的准确率如表1所示。

表1 判断常见图形的维数
由表1得出许多学生不能正确区分一些常见几何图形的维数,只有35%的学生明确曲线是一维的,仅40%的学生能指出域是二维的,不到30%的学生认为曲面是二维的。学生可能认为曲线和域都是平面图形,在解析几何上都是在二维的直角坐标系上表示出来的,所以它们都同是二维;相类似地也认为球和球面是同维数的。既然在生活中、教学中偶尔会有维数的说法,而且学生具有某些不正确的维数观,那么在教学中是有必要比较系统地向学生渗透维数的知识,使学生能正确区分各种常见几何图形的维数,适当了解与维数相关的知识。
三、在初中几何教学中渗透维数知识的可行性
全日制义务教育《数学课程标准》(实验稿)建议教学活动必须建立在学生已有的知识经验和主观愿望基础之上。
1.大部分学生的认知结构里有维数。维数是几何图形的性质之一,目前初中数学教材并没有关于维数知识的学习内容。在第二维度的调查中发现,70%学生都接触过维数(见表2),所以他们对“维数”并不陌生,在学习上能够像对其他学习内容一样,心理上不会产生很大的障碍。学生总是用原来的知识来过滤、解释新信息,但是他们不能完全同化不熟悉的新信息。因此,学生的认知结构里有维数为学习提供了同化的基础学习材料,这对于渗透维数知识的教学无疑是一大幸事。

表2 获取维数几何图形的维数知识的途径
2.绝大部分学生有学习维数知识的意愿。在第三维度的调查中发现有 57.5%学生认为很有必要学习维数知识,有 17.5%学生认为有必要学习维数知识,结果表明大部分学生具有倾向学习维数知识的主观意愿(见表3)。学习的主观意愿是对学生学习维数知识起激励和推动作用的动力,可以激发学生学习的积极性和主动性,推动学生努力地、有意义地了解维数知识。所以,学生具有的这个学习意愿在渗透维数知识的教学中可以起到事半功倍的教学效果。
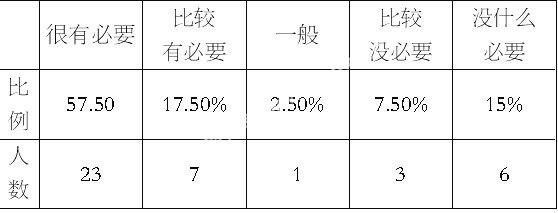
表3 数学课学习维数知识必要性
四、在初中几何教学中渗透维数知识的教学建议
1.不宜喧宾夺主。维数知识是作为几何教学中的一种数学文化的补充形式穿插在授课内容中的,不能喧宾夺主,应以完成教学计划为主。在几何的授课过程中自然引出,不应过分渲染,忽视了正常的教学内容。正确把握好维数知识和课堂教学内容的主次,但也不能因为不能过分渲染,而在教学中草率地一笔带过。课前要精心准备教学设计,根据初中学生的接受能力和旺盛的求知欲,既要交代清楚一般常见图形的维数、简单介绍维数概念的相关知识,还要充分挖掘其中蕴涵的丰富的数学文化意义,努力把维数有形的数学知识和无形的数学文化价值在教学中融合在一起。
2.语言宜通俗化。维数的概念要用到边界和任意小邻域的概念来叙述,初中学生的认知结构里还没有极限的概念,任意小邻域的理解对他们来说是比较抽象的,所以在教学中要采取一种比较通俗的、学生可以接受的语言描述方式。20世纪初,Poincare用通俗的语言指出了维数的概念,这在教学中是适宜引用的。Poincare 认为:若在一条曲线上标定一点,就把曲线“切断”成两部分。一个蚂蚁从一端爬进其中一部分,如不通过这个点,它就无法进入另一部分。也就是说一个点就能阻止蚂蚁继续前进。若在一个曲面上,就不能用点将它“切断”,必须用曲线才能划开曲面为两部分。划分空间一个立体为两部分,则必须用曲面。这就是说一种图形被另一种图形划分,两者是不同维的。图形的边界(也是图形)比该图形的维数低一维。若视点是零维的,曲线即应是一维的,曲面是二维的,立体是三维的。根据这种想法,Menger和Uryon用归纳的方法给出了图形M维数的严格定义。
3.简单介绍分形图形的维数。在讲完了上述的维数内容之后,或许学生就觉得几何图形的维数是整数的,这时还可以给学生来个认知冲击,并不是所有的图形的维数都是整数的,像噪音图、材料的裂缝图等分形图形的维数并不是一维的,而是分数维的。如果学生很感兴趣,那么,分形又是另一个值得开发的数学素材。
数学教学不等于教学数学,而是着眼于人的素质的提高和德智体美诸方面的和谐发展。几何图形的维数蕴涵着丰富的数学意义,数学教师可以挖掘出许多蕴涵其中的教育价值,在渗透教学中做到全面育人。
参考文献:
[1]胡炳生.现代数学观点下的中学数学[M].北京:高等教育出版社,1999.
[2]唐复苏.中学数学现代基础[M].北京:北京师范大学出版社,1988.

