风电场功率曲线异常数据的清洗与建模

曹立新, 刘伟民, 郭虎全

(1. 甘肃省特种设备检验检测研究院, 甘肃 兰州 730050； 2. 兰州理工大学 机电工程学院, 甘肃 兰州 730050)

风电是目前最成熟、发展最快的可再生能源之一.截止2020年底，全球新增装机容量为93 GW，同比增长53%，总装机容量达到743 GW；中国新增装机容量占比达到55.91%，在风电发展中占据重要地位[1].随着风电的迅速发展，为保证风电机组正常运转，风机的日常状态监测成为了重要的研究方向[2].

海上风电远离内陆，风机故障会造成更加严重的经济损失，目前解决此类问题的主要方法是建立高效精确的日常风机工作监控曲线模型[3-4].因此，风电场功率曲线建模成为重要的研究方向.主要包括2部分：1) 风电场风速和功率数据的采集与异常数据清洗，风电场异常数据的识别和清洗不仅可用于功率曲线建模，还能进行风能评估和发电量预测[5]；2) 利用清洗后的数据，建立实时风速-功率曲线状态监控模型，及时发现风机故障信息[6-7].

在风电场异常数据的识别和清洗中，最常用的方法是基于数据方差、中位数和平均值等特征进行清洗.娄建楼等[8]通过降序排列组内功率数据，计算滑差并设置阈值完成异常数据清洗,该方法虽然计算简单方便，但忽略风速-功率曲线上方异常数据，清洗不完全.Shen等[9]通过计算方差变化率等进一步完善了阈值的选择，结果更加精确，但计算较为复杂.此外，基于数据之间距离和密度进行数据剔除也是清洗异常数据的常见方法之一.赵永宁等[10]首先利用四分位法剔除分散异常数据，然后利用k-means聚类方法剔除叠加异常数据.朱倩雯等[11]利用临近风场数据和三次样条插值重构缺失数据.Zheng等[12]利用加权距离和局部离群因子算法(LOF)来实现异常数据的识别和剔除.Zhao等[13]首先利用2次四分位法消除稀疏异常数据，然后利用基于密度的聚类方法消除叠加异常数据.Long等[14]将风速功率的散点图转换为二值图像，通过提取图像特征完成异常数据识别和清洗.Wang等[15]和Gill等[16]基于Copula函数建立概率功率曲线，并通过提取风场异常数据特征，建立了异常数据判断准则.

对风电场风速-功率曲线进行建模和分析，可以为风机设计、风场选址、评估机组运行性能和检测风机是否存在故障等提供参考[17-19].最常用的功率曲线模型是高次多项式模型[20]，Carrillo等[21]通过比较三次多项式、指数函数和三次幂函数，进行建模精度对比.基于假定形状的风电功率曲线虽然求解简单，但精度不高，Thapar等[22]利用最小二乘法和三次样条插值曲线拟合方法进一步提高了拟合精度.Taslimi-Renani等[23]提出利用修正双曲正切的参数模型拟合风电功率曲线，并借助粒子群优化等进化算法进行参数估计，通过对比验证了该模型的有效性.此外，由于Logistic函数形状与风电功率形状相似，近年来四参数Logistic和五参数Logistic也被广泛应用于风电功率曲线建模，并表现出了较好的拟合精度[24-26].非参数模型也被广泛应用于功率曲线建模[25].Manobel等[27]通过高斯过程预先过滤异常数据，然后利用神经网络建立风电功率曲线.杨茂等[28]利用混合半云模型对风电功率曲线进行建模和数据挖掘.

本文将风速-功率散点图中的数据进一步分类，根据异常数据的特征采用组内方差和四分位分步进行数据清洗.该方法简单高效，适用于不同风场和不同风机，具有良好的适应性.在此基础上,利用高次多项式和四参数Logistic进行风速-功率曲线建模，通过比较均方根误差(RMSE)、和方差(SSE)以及决定系数(R2)优选最佳模型.

1 风电场异常数据特征及其分类

风电机组运行数据可通过安装在风电场的数据采集与监视控制(SCADA)系统得到.在数据采集过程中,极端天气、通讯故障、测量仪器损坏、风电机组故障以及弃风限电等均会造成大量异常数据[7].根据产生原因和分布特征，风电场异常数据可以分为3类：顶部稀疏异常数据、中部稀疏异常数据和底部叠加异常数据.不同类型的异常数据分布如图1所示.

图1 异常数据分类Fig.1 Outlier classification

顶部稀疏异常数据是散乱分布在功率曲线上方的数据点，其产生的原因是通信故障或风速计传感器故障.因为在风场测量准备期间，仔细核对了测量仪器，所以这种现象不会大量出现;此类异常数据一般出现在低风速区间，其功率值高于正常功率值，在总体数据中占比较少.中部稀疏异常数据是散乱分布在功率曲线下方的异常数据，其产生的原因包括通信故障、极端天气、传感器记录错误和弃风限电等;此类异常数据一般在正常数据下方波动，无法真实反映风机真实工作性能.底部叠加异常数据是叠加分布在风速-功率散点图底部的大量异常数据，其产生的原因包括风机故障停机或维护、测量设备故障和弃风限电等;此类异常数据存在风速，但功率值在零附近，在总体数据中占据了很大部分，尤其在较为偏远的“三北”地区，底部叠加异常数据更为严重.

2 理论功率曲线和异常数据对功率曲线影响

风机通过叶片吸收风能并转化为机械能，再利用发电机发电实现能量转换，达到使用要求.风机叶片捕获的理论功率P为

P=0.5ρACpv3

(1)

式中：ρ空气密度，kg/m3；A为叶片扫掠面积，m3；Cp为理论风能利用系数，最大值为0.593；v为风速，m/s.

风力发电机的工作状态可以分为4部分：切入风速之前功率为零，切入风速与额定速度之间功率满足式(1)，额定速度与切出速度之间功率保持额定功率不变，超过切出速度后功率为零.风机实际输出功率P(v)为

(2)

式中：v1为切入速度，m/s；v2为额定速度，m/s；v3为切出速度，m/s；p(v)为切入风速和额定风速之间的可变功率，kW；pr为额定功率，kW.

风机理论功率曲线如图2所示.

图2 风机理论功率曲线Fig.2 The theoretical power curve of the wind turbine

异常数据的存在会造成功率曲线模型不准确，无法进行风机检测和功率预测.尤其当异常数据数量超过正常数据时，问题更加严重.在此情况下，采用IEC标准进行功率曲线建模时，发现拟合功率曲线明显偏离理论值[29].图3是采用Bin法对未进行异常数据剔除便进行拟合得到的风电功率曲线.可以看出，若不进行异常数据清洗，则无法进行有效建模.

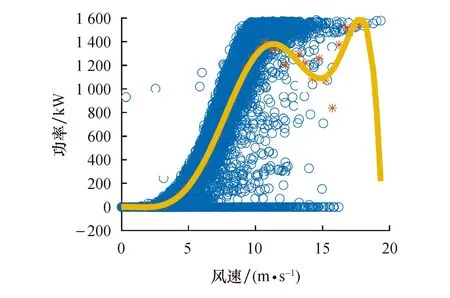
图3 应用未处理数据得到的功率曲线

3 异常数据剔除方法和原理

3.1 组内标准差算法

为便于分析和异常数据识别，按照IEC标准，对风场数据按照0.5 m/s风速区间进行划分.任一区间W为

W={(v1,p1),(v2,p2),…,(vi,pi),…，(vn,pn)}

i∈(1,n)

(3)

式中：vi为W区间内第i个数据对应的风速，m/s；pi为vi对应的功率，kW.

传统组内标准差算法是基于整体平均值来计算的，即

(4)

式中：s为第i个点的标准差；¯p为区间W内功率的平均值；n是区间W内的样本总数.

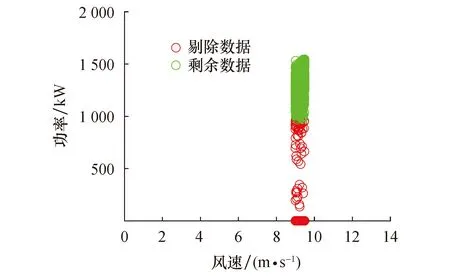
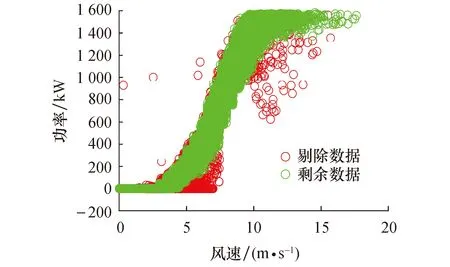
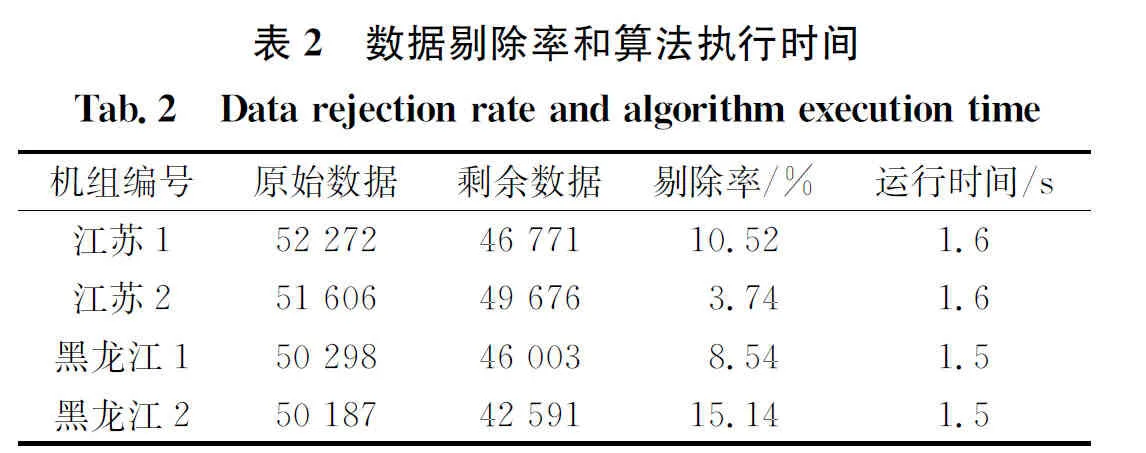
由于底部叠加异常数据的存在，区间W的平均值无法真实反映功率平均值，所以无法利用传统的标准差计算方法完成数据清洗.另外，根据风电场异常数据特征和分类，可以确定顶部稀疏异常数据占比较小，不会大量存在.因此，可将区间W内的数据按照功率从大到小排列，记为U= {(x1,y1), (x2,y2), … , (xi,yi), … , (xn,yn)},其中，yi

(5)

最后，需要设置阈值E，当滑差值超过所设阈值时判定为异常数据.

在进行分析时，常选取额定风速前的区间[13].本文以[9.0～9.5]风速区间为例进行滑差值计算和阈值确定，原始数据中位于该区间内的数据点共有1 434个，降序排列后计算滑差值.图4是该区间的滑差值变化曲线，通过分析可以找出突变点为(1 295，118)，即滑差阈值E为118.因此，当滑差值超过118时可剔除相应的数据.

图4 滑差曲线

图5是利用滑差值剔除异常数据后的结果.可以看出，底部叠加的异常数据大部分被剔除掉，但中部稀疏异常数据未清理完全，且顶部稀疏异常数据还未被清理.将该区间的滑差阈值分别应用于其他区间，可以得到应用滑差法剔除异常数据后的结果，如图6所示.

图5 风速区间[9.0-9.5]内功率散点分布Fig.5 Distribution of power scatter points in the wind speed range [9.0-9.5]

图6 滑差法清洗后的结果Fig.6 Results after cleaning by slip variance method

可以看出，用上述方法进行异常数据剔除时，将某个特定区间的滑差值突变点作为阈值应用在其他区间效果并不理想.因此，仅凭滑差法进行异常数据剔除无法达到理想效果，需要借助其他方法进一步提高异常数据的清洗效果.

3.2 四分位算法

四分位算法是将数据平均分成4份，依据3个间断点P1、P2和P3之间的关系进行数据划分.按照升序排列的任一风速区间功率数据P=[p1,p2,…,pn]，其计算过程如下[9,10,13]：

1) 计算中位数P2(第2个中位数)

(6)

2) 计算第1个四分位数P1和第3个四分位数P3

当n= 2k(k= 1, 2,…)时，中位数将原本的数据从中间分为2部分.此时计算第1个和第3个四分位数，并按照式(6)继续求这2部分中位数P′2和P″2(P′2

当n= 4k+ 1(k=1, 2,…)时，有

(7)

当n= 4k+3(k=1, 2,…)时，有

(8)

利用第1个四分位数P1和第3个四分位数P3计算四分位距q,即

q=P3-P1

(9)

通过四分位距q可以计算得到异常数据的内限，即

[Fl,Fu]=[P1-1.5q,P3+1.5q]

(10)

式中：Fl为异常数据区间下限；Fu为异常数据区间上限.

位于内限的数据均为正常数据，四分位法作为稳健统计方法，不受极端异常数据影响，对于异常数据较少的数据集能够较好地完成异常数据识别和剔除.四分位法常用于稀疏异常数据的清洗，但值得注意的是，未经处理的风场数据，由于底部含有大量叠加异常数据，而且数量可能超过正常值，所以无法利用四分位法识别.本文利用滑差法处理后,将底部叠加异常数据进行了初步清理，恰好满足四分位法使用要求.图7是用滑差法处理后的数据进一步利用四分位法进行清洗的效果.

图7 四分位法清洗结果

4 实例分析和算法对比

为验证提出的滑差-四分位法分步剔除异常数据的有效性，本文选取江苏某风场2组数据和黑龙江某风场2组数据进行实验验证.江苏风场数据的记录日期为2019年1月1日至2019年12月31日，风机额定功率1 800 kW，叶轮直径106 m，轮毂高度90 m，切入风速3 m/s，额定风速9.5 m/s，切出风速20 m/s.黑龙江风场数据的记录日期为2019年5月15日至2020年5月14日，风机额定功率1 500 kW，叶轮直径93 m，轮毂高度90 m，切入风速3 m/s，额定风速9.5 m/s，切出风速22 m/s.

表1是异常数据剔除前后利用九次多项式拟合功率曲线的均方根误差，通过数据剔除前后均方根误差对比，验证本文所提方法的有效性.可以看出，该方法面对不同风场的不同风机均表现良好.其中，江苏的2组数据均方根误差分别提高了46.66%和47.49%，黑龙江的2组数据均方根误差分别提高了62.20%和74.88%.相比之下黑龙江的2组数据提升较大，主要原因是：风场较为偏远，没有完善的电力调度策略，弃风限电现象较为严重.

除了均方根误差，运算速度和异常数据剔除率也是重要的评价指标.表2是在PC端MATLAB程序运行时间和数据剔除率.可以看出，平均处理时间为1.55 s，满足工程实际需要.

图8是不同风场利用滑差-四分位法剔除，并采用Bin法取点后利用九次多项式拟合得到的实际风速-功率曲线.与剔除前得到的功率曲线对比，更符合理论功率曲线形状，可以作为风机的日常状态监测模型.

图8 不同风场用滑差-四分位法清洗后的功率曲线

表3比较了九次多项式和四参数Logistic拟合功率曲线结果，引入和方差、均方根误差和确定系数进行评价.可以看出：和方差、均方根误差值越小，拟合效果越好，确定系数则相反;相比四参数Logistic九次多项式拟合效果较好.

5 结论

本文基于风场原始数据中存在的大量异常数据，根据不同异常数据的分布特征划分为3类:顶部稀疏异常数据、中部稀疏异常数据和底部叠加异常数据.采用滑差-四分位法对不同风场进行异常数据筛选和功率曲线建模，引入和方差、均方根误差和确定系数验证该方法的适用性和有效性.主要结论如下:

1) 风场得到的原始数据存在大量异常数据，若不进行筛选就进行功率曲线建模，则无法反映风机真实工作情况，不能作为风机日常状态监测模型；

2) 本文所提滑差-四分位法对不同风场的数据清洗效果显著，滑差法可以筛除底部叠加异常数据和部分中部稀疏异常数据，四分位法可以清洗部分中部稀疏异常数据和顶部稀疏异常数据，具有较强的通用性和有效性，可以为风场电力调度和风机故障检测提供新策略；

3) 数据筛选中无法辨识是否剔除了正常数据，需要进一步提高异常数据识别率；同时，数据清洗效果缺乏评价指标，有待提出新的评价准则；

4) 比较了现有功率曲线建模方法九次多项式和四参数Logistic，发现九次多项式略优，但参数较多，有待提出更加简单精确的函数模型.