基于SSA-VMD和熵的特征值提取方法*

韩星辰，赵柏山，慈贺迪

（1.沈阳工业大学信息科学与工程学院，沈阳 110870；2.吉林大学电子科学与工程学院，长春 130012）

1 引言

滚动轴承作为旋转机械设备的基本核心部件之一，具有易损性高的特点。滚动轴承的振动信号也有着非平稳、非线性[1]的特征，在故障发生早期，会制造较大的噪声干扰，故障信号极易淹没在噪声中。为了能够直接准确地进行故障特征识别，就需要对轴承的振动信号进行故障特征提取。变分模态分解（VMD）方法能够将多分量信号一次性分解成多个单分量调幅或调频信号[2]，从而克服了EMD算法中模态混叠和频率特征不易分辨等问题，使分解出来的各个IMF分量更加清晰，方便后续处理。本研究即是基于这一方法，利用SSA加以优化，并结合熵，提出一种改进的特征值提取算法。

2 基于SSA-VMD和熵的特征提取

改进算法的整体流程如图1所示。在流程开始之初，须采用SSA-VMD方法对信号进行分解。在麻雀搜寻算法（SSA）[3]中，每只麻雀均有三种可能的身份：一是负责觅食的发现者；二是负责跟随发现者进行觅食的加入者；三是预警者，负责警戒侦查，有危险则通知种群放弃食物，一般预警者数量占整个种群的10%～20%。

图1 算法整体流程图

以SSA对VMD进行优化[4-5]的具体实现步骤详细如下：

a.对相关参数初始化，并随机产生[k,α]组合作为麻雀种群的初始位置。

b.计算适应度值并排序，找到当前最优、最差的个体。

c.对种群中的发现者位置进行更新，其位置更新可表示为：

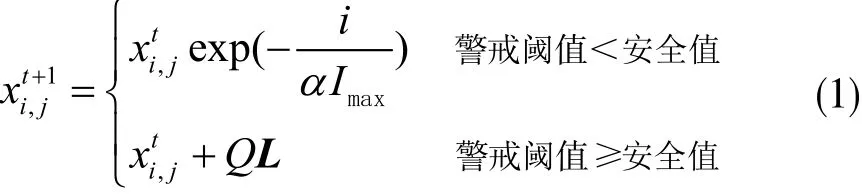
其中，t表示当前迭代次数；IMAX表示最大迭代次数。α表示(0,1]内一个随机数；Q表示服从正态分布的随机数；L表示大小为1×d、所有元素均为1的矩阵。对种群中的加入者位置进行更新，其位置更新可表示为：

其中，A表示大小为1×d、所有元素随机赋值为1或-1的矩阵，A+为A的伪逆矩阵，即A+=AT(AAT)-1。xp为发现者所处最佳位置；xworst为全局最差位置。对种群中的预警者位置进行更新，表示为：

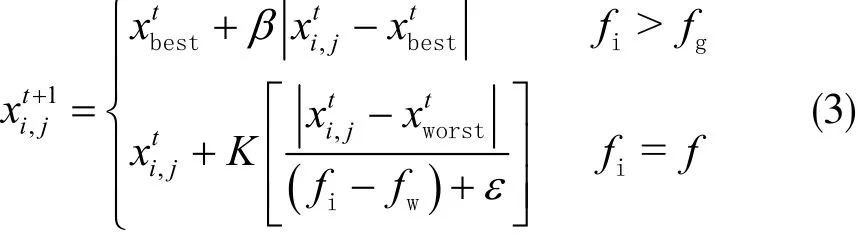
其中，K、β为步长控制参数；xbest为全局最优位置；fi为麻雀适应度值；fg为全局最佳适应度；fw为全局最差适应度；ε表示最小常数。

d.判断是否终止，若不能终止，重复执行步骤b至d。

e.输出最优个体位置[k,α]。

包络熵值与信号中特征信息含量成正比，故将包络熵作为SSA-VMD的适应度函数。包络熵的定义为：

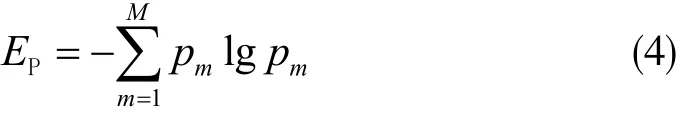
其中，pm表示对信号x(m)利用Hilbert解调变换的包络信号归一化处理。

利用峭度筛选分解后所得的IMF分量。峭度值通常是对信号中包含故障信息量的度量手段[6]。峭度越大，故障信息越多。峭度值的定义可以表示为：

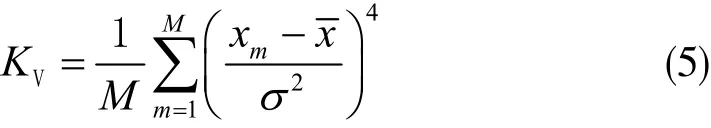
其中，x为信号xm的均值；M为采样长度；σ为信号xm的标准差。对于正常轴承，KV=3。

至此，便可以构成特征向量矩阵，将能够检测信号是否存在动力学突变的排列熵与能够反映信号复杂程度的样本熵共同作为特征因素。

假设有时间序列{x(1),x(2),...,x(m)}，排列熵可以表示为：

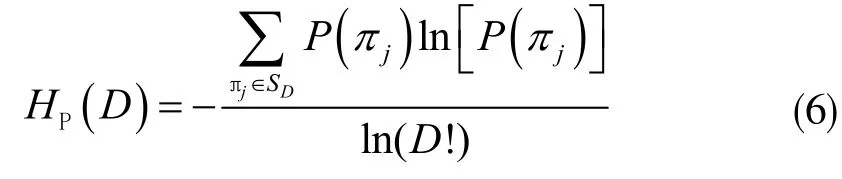
其中，D表示嵌入维数，将所有的可能排列集合记做SD；P(πj)表示每一类πj序列的概率。

样本熵[7]可表示为：

其中，r为相似容限阈值；Cm(r)与Am(r)分别表示构建m、m+1维向量中向量数d[xi+1,xj+1]＜r与总向量数的比值的平均值。

3 实验分析

采用美国凯斯西储大学轴承数据（CWRU）进行实验分析。实验中采用数据的转速为1797r/min，信号采样频率为12kHz。数据包括四种：正常状态、内圈故障、外圈故障、滚动体故障。

令采样长度N=1024；每种数据100个样本，共计400个样本。以滚动体故障数据为例，设种群大小n=30，最大迭代次数IMAX=200，安全值为0.6，发现者比例为种群的70%，预警者比例为种群的20%，其他为加入者。令α∈[100,4000]，K∈[2,15],取噪声容限为0，收敛容差为1.0×10-7，滚动体故障信号经SSA-VMD方法处理后，所得模态分量的时域图与频谱图如图2所示。

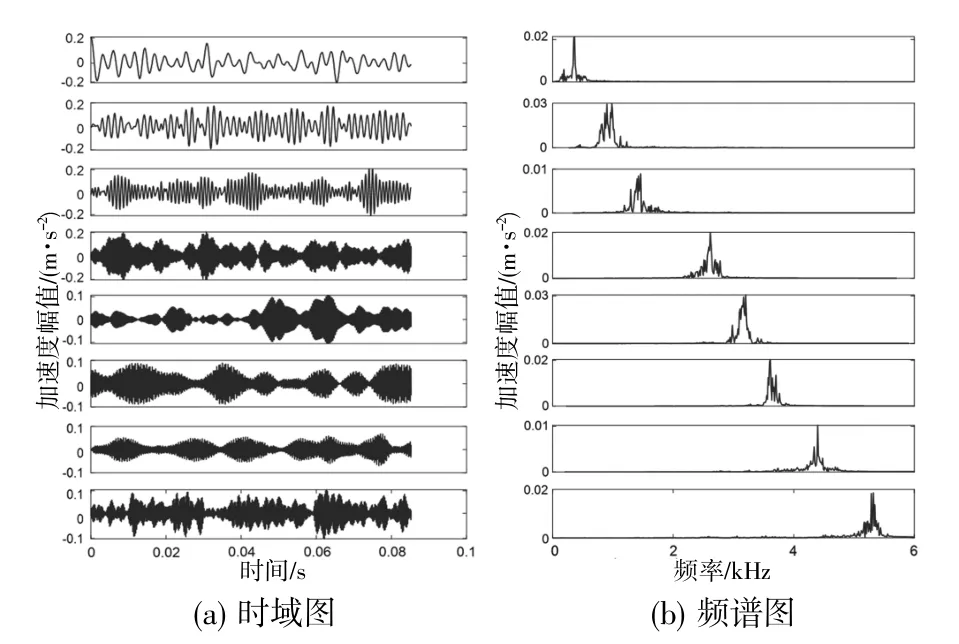
图2 滚动体故障信号SSA-VMD处理效果

由图可知，滚动体故障信号经过SSA-VMD处理后，获得了信号分解出来的8个模态分量，每个分量都有一个对应的中心频率。为进一步验证SSAVMD方法的有效性，令其与PSO-VMD和GA-VMD进行对比。同样以轴承的滚动体故障数据为例。令遗传算法中交叉概率为0.8，变异概率为0.2，粒子群算法中学习因子皆为1，其他参数均与SSA-VMD相同，并且同样将包络熵作为适应度函数。三种算法的适应度函数迭代对比情况如图3所示。

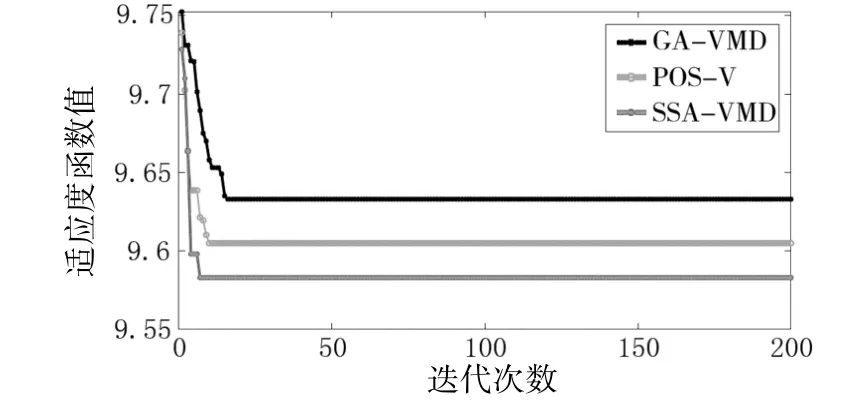
图3 各算法适应度函数对比

可见，SSA-VMD算法的寻优速度优于POSVMD与GA-VMD。由适应度函数值可知，经SSAVMD方法处理后所得的IMF分量中，噪声含量少于POS-VMD与GA-VMD。

SSA-VMD、POS-VMD、GA-VMD三者的各模态分量的中心频率如图4所示。由实验结果可见，信号经过SSA-VMD方法分解所得到的各模态中心频率之间相对独立，有效地避免了模态混叠现象，得到了较为单纯的本征模态。

图4 各算法中心频率分量对比

综上可知：SSA-VMD方法在迭代速度、中心频率分布与所得包络熵局部最小值方面均优于POSVMD与GA-VMD。

实验中也得出了不同状态下的SSA-VMD最优参数，详细结果如表1所示。

表1 SSA-VMD最优参数

计算各个模态的峭度值，由于峭度值越大，包含冲击信息越明显，因此选用峭度值最大的三个IMF分量，计算排列熵与样本熵。轴承的四种状态分别对应1、2、3、4的标签，每种状态共100个样本。以此计算故障数据所对应的排列熵[HP1,HP2,HP3]与样本熵［ES1,ES2,ES3］，共同组成特征向量矩阵[HPES]100×6。

诊断模型选用全局搜索能力强、迭代速度快的WOA-SVM[8]，将上述三种方法提取到的特征向量输入到该诊断模型中进行诊断。

令种群数量n=30；迭代次数为200；将K重交叉验证的准确率称为训练准确率，并令其为适应度函数，将已经训练好的模型上的分类准确率称为识别准确率，令K=5；在每种数据样本中随机选取75组作为训练样本，余下25组作为测试样本。

经实验，得到POS-VMD、GA-VMD、SSA-VMD三种算法的诊断结果图，如图5所示。具体的诊断结果数据如表2所示。

图5 诊断结果图

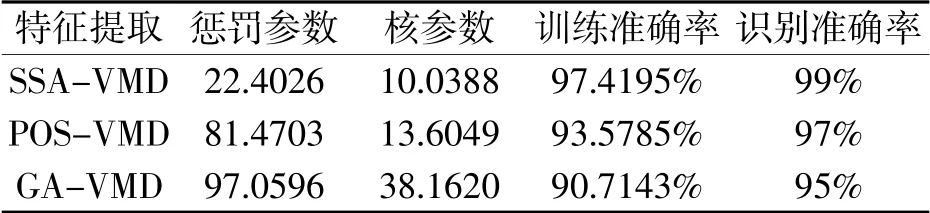
表2 诊断结果数据

可见，与其他两种方法相比，SSA-VMD的识别准确率与训练准确率均有所提高。

4 结束语

改进算法基于SSA-VMD和熵的特征提取方法，将包络熵作为适应度函数，根据峭度筛选IMF分量，选用排列熵与样本熵共同组成特征向量。通过与POS-VMD和GA-VMD的实验对比，证明了经SSA-VMD分解后的IMF分量更加清晰、独立，其寻优速度与寻优结果均更为优越。将三者提取出的特征向量使用同一诊断模型进行分类识别，SSA-VMD的识别准确率与训练准确率均高于POS-VMD与GA-VMD，表明SSA-VMD和熵相结合的方法能够更有效的进行特征提取，提高识别准确率。