基于MCKD和峭度的液压泵故障特征提取
何庆飞,王旭平,李禹生
(1.西京学院机械工程学院,陕西西安 710123;2.火箭军工程大学作战保障学院, 陕西西安 710025;3.平高集团有限公司, 河南平顶山 467000)
0 前言
液压系统是大型工程机械的重要组成部分,对其核心部件之一液压泵进行研究具有重要意义[1-2]。常用的研究方法是对液压泵采集信号进行分析,但是液压泵结构复杂、振动源众多,采集信号受噪声影响严重,为有效获取真实信息,必须对采集信号进行去噪和特征提取。最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution, MCKD)[3-5]是用相关峭度为评价指标,其降低了信号的噪声成分,提升了信号的峭度。文献[6-9]将MCKD应用于轴承故障特征信号提取,减弱了噪声成分,加强了轴承故障信号中周期性冲击成分,提取出明显的故障特征,达到对轴承故障精确诊断。峭度是一个经典的非高斯性度量指标。一般,随机信号的非高斯性程度既可以使用峭度绝对值来度量,也可以使用峭度的平方值来度量。因此,文中提出基于峭度(或峭度绝对值,或峭度平方值)的特征信息提取方法,利用峭度(或峭度绝对值,或峭度平方值)来度量机械信号的非高斯性程度,进而表征机械设备的运行状态信息。文献[10-11]利用峭度来进行机械设备的故障特征提取及诊断,取得了一定的效果。因此,文中提出了先利用MCKD对液压泵振动信号去噪,然后利用峭度进行故障特征提取方法,为液压泵的状态监测和故障诊断提供依据。
1 最大相关峭度解卷积
液压泵状态信号中存在的噪声将减弱信号的识别性。而MCKD 用相关峭度为评价指标,降低了信号中的噪声成分,提升了原始信号的峭度,充分突显了液压泵故障信号中被噪声淹没的周期冲击成分。
假设采集的液压泵振动信号表示为
y=r·x+e
(1)
式中:y为实际采集信号;x为液压泵状态信号;r为传输路径衰减响应;e为噪声信号。
MCKD算法的根本就是求解一个FIR( Finite Impulse Response) 滤波器最优解的过程。通过实际采集信号y恢复状态信号x,从而抑制噪声和突出故障冲击成分,即:
(2)
式中:r=[r1,r2,…,rL];L为滤波器的长度。
MCKD 实质是以相关峭度为评定指标。信号y相关峭度定义为
(3)
式中:M为位移数;T为冲击信号的周期。 MCKD算法以相关峭度最大化为目标函数:
(4)
即求解方程:
(5)
求解的滤波器系数用矩阵形式表示如下:
(6)
式中:
式中:t= 0,T,2T,… ,mT。
将得到的滤波器系数r代入公式(2),即得信号x。
2 峭度(Kurtosis)准则
为了度量随机信号的非高斯性程度,必须定义一个定量化的非高斯性指标。峭度就是一个经典的非高斯性度量指标。
2.1 四阶矩
考虑一个具有概率密度函数py(y)的随机变量y,它的第j阶矩αj定义为
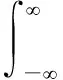
(7)
相应地,随机变量y的第j阶中心矩μj定义为

j=1,2,…
(8)
由此可见,中心矩围绕着随机变量y的均值my计算,均值my等于随机变量y的一阶矩α1。
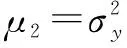
2.2 峭度
峭度是随机变量的一种四阶累积量,定义为
Ku(y)=E{y4}-3(E{y2})2
(9)
式中:y的均值是零。假定y是标准化的,即其方差为1,则有:
Ku(y)=E{y4}-3
(10)
由式(10)可知,峭度在本质上是随机变量四阶矩的一种规范化形式。一般,高斯随机变量y的四阶矩为3(E{y2})2,因此它的峭度为零。大部分(并不是所有的)非高斯随机变量的峭度为非零值。
峭度无论是从计算上还是从理论上都非常简单。从计算的角度,若样本数据的方差不变,峭度可用样本数据的四阶矩来估计:
(11)
在理论上,峭度的一个有用特性是它的可加性,若y1和y2是统计独立的随机变量,那么有:
Ku(y1+y2)=Ku(y1)+Ku(y2)
(12)
这里要注意,可加性质对于随机变量的四阶矩并不成立。此外,峭度的另一个有用特性是它的比例性,若有标量参数α,则有:
Ku(αy)=α4Ku(y)
(13)
由此可见,峭度不是线性的。
3 基于峭度的特征信息提取方法
从统计意义上来说,随机变量的峭度是一个能够指示它的非高斯性程度的最简单的量。通常,随机变量的非高斯性既可以用峭度的绝对值来度量,也可以使用峭度的平方,因此,峭度的绝对值(或平方)在统计意义上是一个随机变量非高斯性的自然度量指标。峭度的绝对值(或平方)越大,说明随机变量的非高斯性越强。
因此,本文作者提出基于峭度(或峭度绝对值,或峭度平方值)的特征信息提取方法,利用它来度量机械信号的非高斯性程度,进而来表征机械设备的运行状态信息。
假设机械设备的传感器观测信号是一组M通道的混合信号,那么基于峭度的故障特征信息提取就是由M通道的混合信号来提取它的峭度基故障特征信息向量。基于峭度的故障特征信息提取方法的具体步骤为:
(1)令j=1;
(2)标准化第j通道混合信号xj,使得E(xj)=0,σxj=1;
(3)计算混合信号xj的峭度(峭度平方值,或峭度绝对值);
(4)令j=j+1,如果j≤M,返回步骤(2);
(5)由M通道混合信号的峭度值构成一个M维的故障特征信息向量。
4 试验研究
液压齿轮泵试验台架和加速度计的设置如图1所示。液压齿轮泵在各个故障模式下的一组传感器观测信号x(t)=[x1(t),x2(t),x3(t),x4(t)]T。

图1 液压齿轮泵试验台架和加速度计的设置
在液压齿轮泵的各个故障模式下,由其中任一传感器观测信号x(t)可以得到一个四维的峭度基故障特征信息向量,一个四维的峭度绝对值基故障特征信息向量和一个四维的峭度平方值基故障特征信息向量。
由得到特征信息可知,峭度(或峭度绝对值,或峭度平方值)基故障特征信息向量具有很好的聚类划分特性,即它们的类间差异显著而类内聚类集中,而且数值也比较稳定。例如在液压齿轮泵的各个故障模式下,峭度绝对值基故障特征信息向量的一维数值分别集中在区间(1.4, 1.7)、(0.9, 2.0)和(0.2, 1.0);二维数值分别集中在区间(0.9, 1.6)、(0.01, 0.1)和(0.4, 0.9);三维数值分别集中在区间(2.0, 5.1)、(0.4, 0.9)和(1.1, 4.0);四维数值分别集中在区间(1.5, 1.8)、(0.7, 1.9)和(0.03, 0.4);其中,最大的区间范围为3.1,最小的区间范围为0.09。因此,峭度(或峭度绝对值,或峭度平方值)基故障特征信息向量可以很好地区分和识别液压齿轮泵的各个故障模式。横向比较可知,相比峭度和峭度平方值,峭度绝对值基故障特征信息向量的聚类划分特性更好,主要因为:(1)峭度值有正有负,而且数值分散,这使得峭度基故障特征信息的类内聚类特性有所弱化;(2)由于平方运算的作用,小的峭度值更趋于集中,大的峭度值更趋于分散,这使得峭度平方值基故障特征信息的类间差异特性有所弱化。因此,在应用中应该更多地考虑使用峭度绝对值基故障特征信息。
峭度(或峭度绝对值,或峭度平方值)基故障特征信息向量的二维平面分布(第一维和第二维,即1号测点和2号测点)和三维空间分布(第一维、第二维和第四维,即1号测点、2号测点和4号测点)如图2所示。
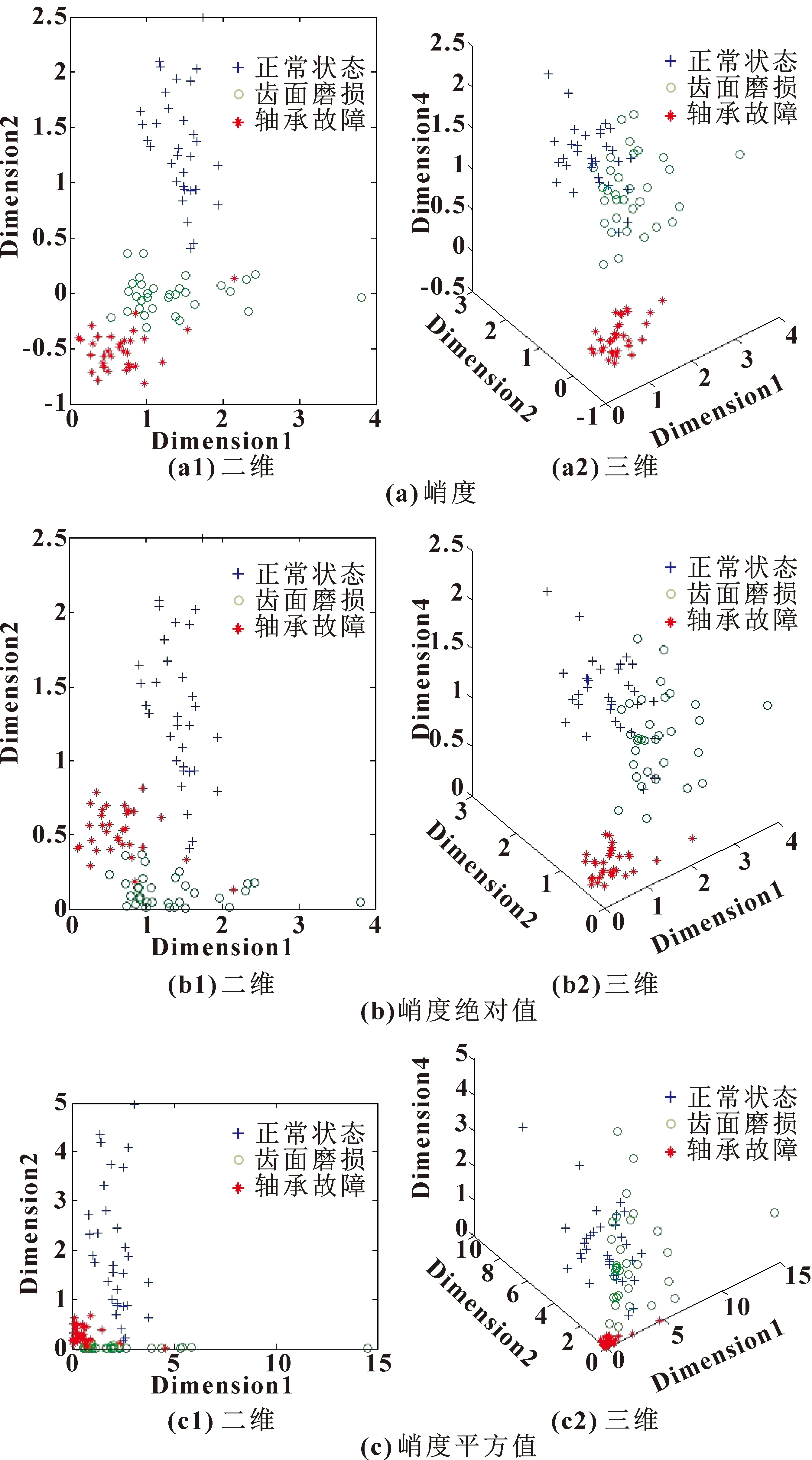
图2 故障特征向量分布
图2所示的峭度基故障特征信息向量分布进一步表明:基于峭度(或峭度绝对值,或峭度平方值)的故障特征信息向量具有非常好的聚类划分特性,而且数值相当稳定。这说明基于峭度的特征信息提取方法是有效的。
5 结语
(1)利用MCKD算法对采集信号初步分析,突出信号中的原始冲击成分并进一步去噪,使得信号的信噪比进一步提高,提高了齿轮泵状态监测和故障诊断精度。
(2)提出基于峭度(或峭度绝对值,或峭度平方值)的特征信息提取方法,利用它度量机械信号的非高斯性程度,进而表征机械设备的运行状态信息。结果表明:基于峭度(或峭度绝对值,或峭度平方值)的故障特征信息向量具有非常好的聚类划分特性,而且数值相当稳定。这说明基于峭度的特征信息提取方法是有效的。
(3)峭度值有正有负,而且数值分散,这使得峭度基故障特征信息的类内聚类特性有所弱化;由于平方运算的作用,小的峭度值更趋于集中,大的峭度值更趋于分散,使峭度平方值基故障特征信息的类间差异特性有所弱化。因此,在应用中应该更多地考虑使用峭度绝对值基故障特征信息。

