谱峭度在轴承故障振动信号共振频带优选中的应用

于明奇，夏均忠，陈成法，汪治安，刘鲲鹏

(1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通学院 军用车辆系，天津 300161)



谱峭度在轴承故障振动信号共振频带优选中的应用

于明奇1，夏均忠2，陈成法2，汪治安1，刘鲲鹏1

(1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通学院 军用车辆系，天津 300161)

在滚动轴承故障振动信号分析中，为减少采集信号共振频带对解调效果的影响，利用谱峭度方法确定共振频带的带宽和中心频率。首先解释谱峭度的含义，分析基于短时傅里叶变换的谱峭度算法的不足；然后提出快速峭度图和突起度图两种改进方法，并分析其特点；最后通过仿真和试验手段，对比分析它们在振动信号共振频带优选中的应用效果。结果表明，突起度图在信噪比较低的情况下，对共振频带的辨别能力优于快速峭度图。

滚动轴承；故障诊断；谱峭度；快速峭度图；突起度图

滚动轴承广泛用于旋转机械中，其运行状态是否正常往往直接影响整台设备的性能，因此对滚动轴承技术状态监测和早期故障诊断具有重要意义。滚动轴承通常由内圈、外圈、滚动体和保持架组成，当其中某一部分表面发生局部故障时，产生的脉冲会激起轴承及其相邻部件的共振，产生调制现象，这使得采集到的振动信号中包含多个共振频带[1]。为获取更好的解调效果，在解调前往往需要选取最优共振频带，以增强故障特征提取效果。

谱峭度(Spectral Kurtosis)及其基于短时傅里叶变换(short-time fourier transform，STFT)的算法提出以来[2]，常用来确定最优共振频带的中心频率和带宽，但是基于STFT的谱峭度计算过程中，只使用一个固定窗，确定的中心频率和带宽不一定最优[3]。Antoni引入峭度图(Kurtogram)概念，提出了快速峭度图(Fast Kurtogram),使谱峭度得到迅速应用[4]，但在信号信噪比较低或者含有随机脉冲噪声等情况下容易失效。为此，增强或改进方法不断提出，其中，Tomasz Barszcz等首先尝试转变谱峭度的计算对象，提出了突起度图(Protrugram)方法，取得了更为理想的效果[5]。

1 谱峭度

Antoni从Wold-Cramer表达式角度提出非平稳信号谱峭度的定义，并被广泛认可。Wold-Cramer表达式可以将任何零均值非平稳随机过程x(n)分解为

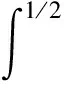
(1)

式中：dZx(f)为正交谱增量；H(n,f)为x(n)在频率f上的复包络。

谱峭度定义为四阶归一化累积量：

(2)

基于短时傅里叶变换的谱峭度计算方法为

(3)

式中：KY(f)为谱峭度的估计量；fs为采样频率；fd为脉冲重复速率；KX为脉冲波动强度；Nw为STFT窗口长度；γ4w为分析窗平方的时间—带宽积；ρ(f)为信号的信噪比。

该算法的提出使谱峭度得到实际应用，但利用STFT分解信号时，只使用一个固定窗，因此只分析了部分信号，计算出的谱峭度不是真正意义上的“全域”谱峭度，确定的中心频率和带宽不一定最优。

针对该算法存在的不足，引入了峭度图的概念，并利用准解析滤波器组代替STFT，提出了快速峭度图。

2 快速峭度图

2.1 快速峭度图算法

对于非平稳过程，谱峭度的计算依赖估计量频率分辨率的选择，谱峭度可以看作是频率和频率分辨率(f,Δf)的函数，因此计算谱峭度的过程就转化为如何在既定频率上选取频率分辨率的问题。为便于表达，用峭度图表示(f,Δf))平面上的谱峭度。基于树状多速率滤波器组结构的快速峭度图算法为：

(1)设置一个低通标准滤波器h(n)，截止频率为fc=1/8+ε(ε≥0)，由h(n)构造频带低通滤波器h0(n)和高通滤波器h1(n)，表达式为

h0(n)=h(n)ejπn/4
h1(n)=h(n)ej3πn/4

(4)

频带位置分别为[0∶1/4]和[1/4∶1/2]。

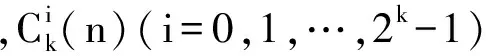
(5)

式中：i=0，1，…，2k-1；k=0，1，…，K-1。

依据式(5)，可以得出(f，Δf)平面上频段(fi,Δfk)的峭度图。

通过上述算法，峭度图可以得到快速计算，但在一些窄带瞬态采样时明显过宽，进而确定的共振频带不是十分精确。为此，额外添加了3个准解析带通滤波器，提出了滤波器组的1/3-二叉树结构，从而在(f,Δf)平面上的采样范围得到明显改善，并且未影响计算速度。

2.2 快速峭度图算法改进

快速峭度图提出后得到迅速应用，但在信号存在下列情形时能力受到限制：

(1)信号的信噪比较低，尤其是含有高峰值的非高斯噪声；

(2)信号存在随机脉冲噪声；

(3)故障脉冲重复速率较高。

通过以下3种方式对快速峭度图进行改进，增强快速峭度图的应用效果。

(1)与其他处理方法结合，增强快速峭度图应用效果[6-9]。

(2)改进分解方法。如利用小波包变换、经验模式分解等替代STFT、准解析滤波器组进行分解，从而达到改进效果[10-13]。

(3)通过改变谱峭度计算对象来改进算法。如由计算包络信号的谱峭度得到计算包络谱、功率谱、平方包络谱等的谱峭度[14-15]。Tomasz Barszcz和Adam Jabonski首先在这方面做出了尝试，由计算时域信号的谱峭度转变为计算经解调后的信号包络谱的谱峭度，提出了突起度图方法。

3 突起度图

谱峭度定义为四阶标准矩，即为：K=μk/σk，其中，μk是关于数列均值的四阶矩，σk是标准差。对于矢量X=[X1，X2，…，XN]，谱峭度值计算方法为

(6)

突起度图中谱峭度的意义在于表征信号中脉冲突起强度，在信号中“突起”数目一定时，其幅值离散程度越大，峭度值也就越大，从而可以确定最大峭度值下共振频带的中心频率，进而确定最优共振频带。

突起度图算法流程如图1所示。首先确定最优带宽Bw，带宽选择满足两个约束条件：①尽可能“窄”，要满足信号中只包含寻找的故障特征信息，避免引入过多噪声；②尽可能“宽”，以支持多组故障轴承同时诊断，提高运算效率，这在工业应用中至关重要。然后设置迭代步长step(步长越小，精度越高，但运算时间增加)，确定迭代范围[Bw/2，fs/2](fs为采样频率)，以Bw/2为初始中心频率fc，利用带通滤波器选取频带[fc-Bw/2，fc+fs/2]，计算该频带包络谱上的谱峭度值，按此循环，直至中心频率为fs/2。最后取其最大谱峭度值所对应的中心频率，即为最优共振频带中心频率。

图1 突起度图算法流程

4 仿真分析

构造周期性振动脉冲仿真信号。单周期脉冲仿真信号x(t)表达式为

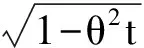
(7)

式中：t为采样时刻；fn为载波频率，fn=1 700Hz；x0为位移常数，x0= 3；θ为阻尼系数，θ=0.1。

设置重复周期T= 0.01s，即故障特征频率fm=100Hz，生成周期性振动脉冲信号，如图2(a)所示。添加高斯白噪声(信噪比SNR=-10dB)，其加噪仿真信号如图2(b)所示。

利用快速峭度图、突起度图分别对加噪仿真信号进行处理，结果如图3、图4所示。图3中颜色深度代表谱峭度值大小，在中心频率fc=2 906.25Hz、带宽Bw=187.5Hz处峭度值最大，其值为0.1，因此，快速峭度图确定的最优共振频带中心频率为2 906.25Hz，带宽为187.5Hz。

在突起度计算过程中，为便于之后的解调分析，选择包含故障特征频率3至4次谐波的带宽，设置带宽Bw= 400Hz>3fm，同时为兼顾计算速度，并不影响识别效果，选择迭代步长step=100Hz。图4中，曲线值代表不同中心频率下的峭度值，在1 600Hz中心频率处谱峭度值最大，其值为0.016 5，因此，突起度图所确定的最优共振频带中心频率为1 600Hz，带宽为400Hz。

(a)仿真信号

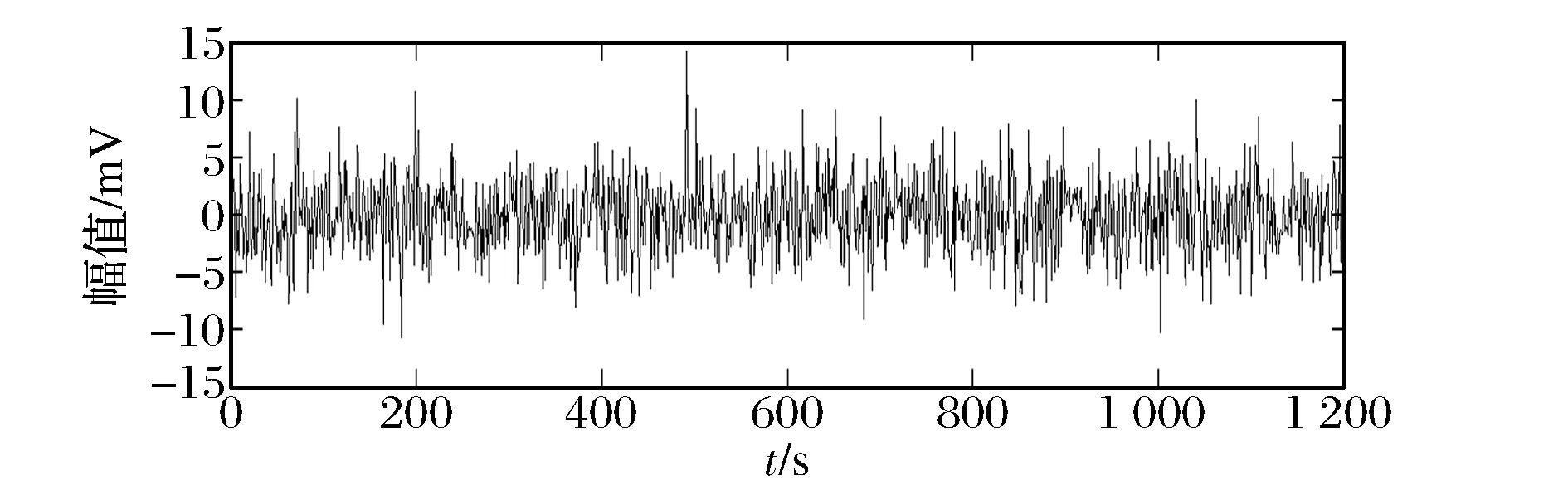
(b)加噪仿真信号图2 仿真信号时域波形

图3 加噪仿真信号快速峭度图

图4 加噪仿真信号突起度图

分别应用快速峭度图、突起度图选取共振频带，滤波后信号的平方包络谱如图5所示。图5(a)中虚线代表故障特征频率及其倍频，图中未能识别与虚线重合的谐波，显然快速峭度图选定的共振频带不正确；在图5(b)中能清晰识别设置的故障特征频率(100 HZ)及其倍频，说明突起度图在信号信噪比较低的情况下对共振频带辨别能力强于快速峭度图。

(a)应用快速峭度图优选共振频带

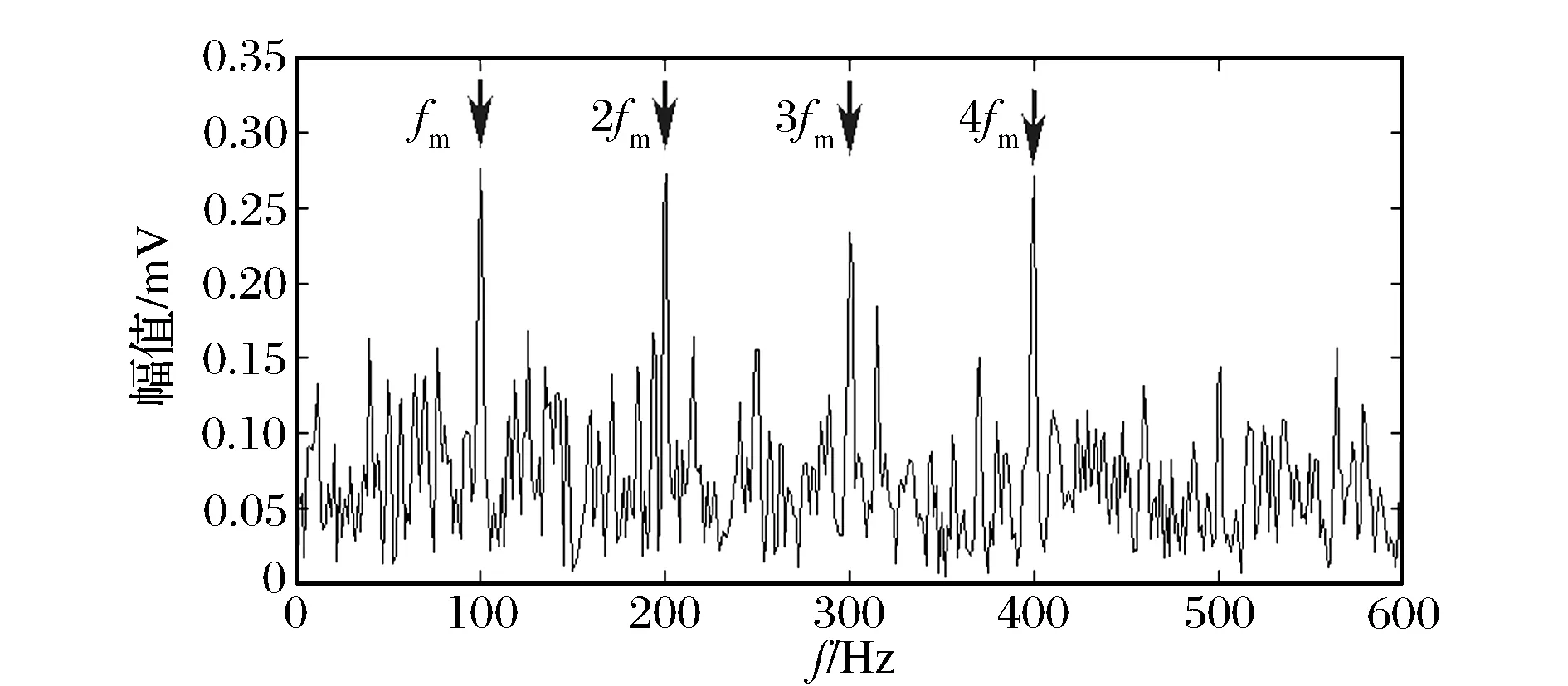
(b)应用突起度图优选共振频带图5 仿真信号平方包络谱

预置带宽的大小直接影响突起度图的辨别能力，分别设置带宽为100 Hz、500 Hz、1 500 Hz、2 500 Hz和4 000 Hz，利用突起度图分别处理仿真信号、加噪仿真信号，确定其对应中心频率(见表1)。仿真信号中由于没有噪声干扰，其中心频率收敛于1 650 Hz。加噪仿真信号下，随着预置带宽的增大，选定共振频带的中心频率先减小后增大。为直观表达带宽选择对突起度图的影响，各自共振频带的包络谱如图6所示，可见带宽设置过小(100 Hz)或者设置过大(4 000 Hz)均使突起度图失效(其包络谱图中难以识别故障特征频率)，当带宽设置为500 Hz时，包络谱中的故障特征频率及其倍频最为清晰，这说明带宽的预置对于突起度图非常重要。可通过支持向量机等方法自适应确定最优预置带宽来改进突起度图方法。

表1 预置带宽及其相应中心频率 Hz

图6 突起度图优选共振频带包络谱

5 试验验证

选取美国Case Western Reserve University公开的轴承故障数据进行故障诊断[6]。试验装置由驱动电机、振动加速度传感器、转矩解码/编码器、联轴器和功率计等组成(如图7所示)。试验轴承为SKF 6205-2RS深沟球轴承，支撑驱动电机驱动端，其技术参数见表2。

图7 试验装置

滚动体直径d/mm节圆直径D/mm内径dm/mm外径Do/mm滚动体数Z接触角α/(°)839255290

对采集的轴承内圈故障振动信号进行共振频带优选，分别得到快速峭度图(如图8所示)、突起度图(如图9所示)。

快速峭度图利用准解析滤波器组计算谱峭度。从图8中可以确定最优共振频带的中心频率fc=2 625Hz、带宽Bw=250Hz，其信号的平方包络谱如图10(a)所示。从图中较难识别轴承内圈故障特征频率(158Hz)及其倍频。

突起度图方法中，设置带宽Bw=500Hz，选择迭代步长step= 100Hz。从图9中可以确定在中心频率fc=3 550Hz时谱峭度值最大，即最优共振频带中心频率fc=3 550Hz、带宽Bw=500Hz，其信号的平方包络谱如图10(b)所示。从图中能够清晰识别轴承内圈故障特征频率(158 Hz)及其倍频(与理论值157.94 Hz不完全一致的原因是由于滚动体随机滑动的影响)。

图8 轴承内圈故障振动信号快速峭度图

图9 轴承内圈故障振动信号突起度图

(a)应用快速峭度图优选共振频带

(b)应用突起度图优选共振频带图10 轴承内圈故障振动信号平方包络谱

通过轴承内圈故障振动信号分析可知，由突起度图确定的共振频带，其平方包络谱中故障特征更为突出，这说明在实际应用中突起度图相比于快速峭度图，在振动信号共振频带优选中较优。

6 结 语

本文首先系统研究了谱峭度的含义，指出基于STFT的谱峭度算法只使用一个固定窗，确定的共振频带不一定最优；针对该算法存在的不足，提出了快速峭度图方法，但其在信号信噪比较低或者含有随机脉冲噪声等情况下容易失效；然后提出改进思路，重点分析了突起度图方法；最后通过仿真和试验手段分析验证了快速峭度图和突起度图在低信噪比以及实际应用中的效果。突起度图方法在信噪比较低的情况下，对共振频带的优选能力较之快速峭度图更为突出，并且在实际应用中取得了更为理想的效果。

应用谱峭度方法可以迅速准确确定最优共振频带，一方面可以增强滚动轴承故障诊断效果，另一方面可以极大提高运算速度，为实现在线技术状态监测提供了可能。如何改进或增强其应用效果依旧是未来研究重点：一是融合多种改进方式；二是改进完善谱峭度指标，比如，引入热力学中熵的概念代替传统意义上的谱峭度等。

[1] RANDALL R B, ANTONI J. Rolling element bearing diagnostics:a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(2):485-520.

[2] ANTONI J. The spectral kurtosis: a useful tool for characterizing nonstationarysignals[J]. Mechanical Systems and Signal Processing, 2006, 20(2): 282-307.

[3] ANTONI J，RANDALL R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines[J]. Mechanical Systems and Signal Processing, 2006, 20(2): 308-331.

[4] ANTONI J. Fast computation of the Kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007, 21(1):108-124.

[5] BARSZCZ T，JABLONSKi A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the kurtogram[J]. Mechanical Systems and Signal Processing, 2011, 25(1): 431-451.

[6] GUO W, TSE P W, A Djordjevich. Faulty bearing signal recovery from large noise using a hybrid method based on spectral kurtosis and ensemble empirical mode decomposition[J]. Measurement, 2012, 45(5): 1308-1322.

[7] 彭畅,柏林,谢小亮.基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断[J].振动与冲击,2012,31(20):143-146.

[8] HUANG W，LIU H，ZHU Z，et al. Fault feature extracting for rotating machinery vibration based on blind deconvolution and spectral kurtosis[J]. Mechanical Systems and Signal Processing, 2012, 43(2): 261-266.

[9] 周智,朱永生,张优云,等.基于MMSE和谱峭度的滚动轴承故障诊断方法[J].振动与冲击,2013,32(6):73-77.

[10] LEI Y G, LIN J, HE Z J, et al. Application of an improved kurtogram method for fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2011, 25(5): 1738-1749.

[11] 程军圣,杨怡,杨宇.基于LMD的谱峭度方法在齿轮故障诊断中的应用[J].振动与冲击,2012,31(18):20-23.

[12] 代士超,郭瑜,伍星,等.基于子频带谱峭度平均的快速谱峭度图算法改进[J].振动与冲击,2015,34(7):98-102.

[13] 彭畅,柏林,刘小峰.基于鲁棒性小波包峭度图的滚动轴承故障诊断[J].振动、测试与诊断,2016,36(1):11-16.

[14] WANG D，TSE P W，TSUI K L. An enhanced Kurtogram method for fault diagnosis of rolling element bearings[J].Mechanical Systems and Signal Processing, 2013, 35(1-2): 176-199.

[15] ANTONI J. The infogram: entropic evidence of the signature of repetitive transients[J]. Mechanical Systems and Signal Processing, 2016, 74(1): 73-94.

[16] SMITH W A，RANDALL R B．Rolling element bearing diagnostics using the Case Western Reserve University data：a benchmark study[J]. Mechanical Systems and Signal Processing, 2015, 64(2): 100-131．

(编辑：张峰)

Application of Spectral Kurtosis in Optimal Selection of Resonance Frequency Bands for Bearing Fault Vibration Signal

YU Mingqi1, XIA Junzhong2, CHEN Chengfa2, WANG Zhian1, LIU Kunpeng1

(1.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China; 2.Military Vehicle Department, Military Transportation University, Tianjin 300161, China)

To reduce the impact of signal resonance frequency bands on demodulation effect while analyzing rolling bearing fault vibration signal, the paper determines bandwidth and center frequency of resonance frequency bands with spectral kurtosis. It firstly interprets the meaning of spectral kurtosis and analyzes the deficiency of spectral kurtosis algorithm based on short-time Fourier transform. Then, it puts forward two improved methods: fast kurtogram and protrugram, and analyzes their characteristics. Finally, it compares their application effect in optimal selection of vibration signal resonance frequency bands. The result shows that protrugram has better distinguishing ability than fast kurtogram on resonance frequency bands in low SNR.

rolling bearing; fault diagnosis; spectral kurtosis; fast kurtogram; protrugram

2016-12-30；

2017-01-13．

于明奇(1991—)，男，硕士研究生； 夏均忠(1967—)，男，博士，教授，硕士研究生导师．

10．16807/j.cnki.12-1372/e.2017.05.010

TN911.23；TB53

A

1674-2192(2017)05- 0042- 06

● 车辆工程 Vehicle Engineering