基于峭度分析的声发射故障检测

沈阳工业大学信息科学与工程学院 何鹏举 于 洋

0 引言

峭度是描述波形尖峰度的一个导出函数，反映出随机变量分布特性的数值统计量，是归一化的四阶中心距，其定义为[1]：

其中，X 为信号的幅值；P( X )为信号的概率密度函数。

离散信号的峭度定义为：

在声发射的特征参数总有一个参数RMS（信号有效值），其定

义为：

因此峭度值K(或峭度系数)可以表示为：

峭度处理会使声发射信号的能量得到放大，削弱较低噪声信号的能量，这样就会很好的凸显声发射信号。

根据相关材料可知，当没有声发射信号只有噪声信号时（材料完好的时候），噪声振动基本服从正太分布，即峭度值K ≈ 3，此时波形服从正太分布；当检测材料出现损伤进而产生声发射信号的时候，峭度值K将会变大[2]。

降噪处理后的信号，经过峭度处理会突出高幅值信号，同时抑制低幅值的信号，声发射信号会得到有效的凸显，且残留的干扰信号也会被进一步抑制。有利于声发射信号的识别和分析[3]。

1 峭度值计算

如图1.1所示，当数列N较小时，数据处理的差别。

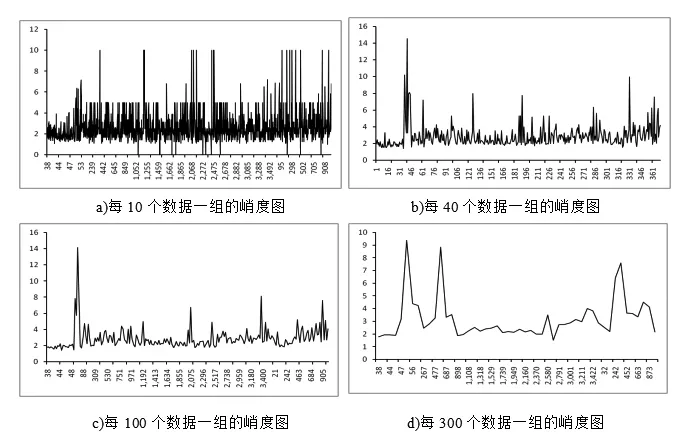
图1.1 少量数据的峭度值计算对比图

由图1.1的四张图可以看出，在图a时，信号的特征不是很明显，基本属于杂乱无章的，看得出噪音干扰信号很多。图b中信号有了初步的抑制和突出的差别，可以明显的看出突出信号。在图c中，波形中期的突变值被进一步抑制，初期的波形得到的突出。在图d中可以清楚看出最开始的一个信号得到了不断的加强，而其他信号都得到了相当大的抑制[5-7]。

在轴承无故障运转时，由于各种不确定因素的影响，振动信号的幅值分布接近正态分布，峭度指标值K≈3；随着故障的出现和发展，振动信号中大幅值的概率密度增加，信号幅值的分布偏离正态分布，正态曲线出现偏斜或分散，峭度值也随之增大。峭度指标的绝对值越大，说明轴承偏离其正常状态，故障越严重，如当其K>8时，则很可能出现了较大的故障。

理论中当K>3.3的时候认为有声发射信号发生，由图3.12所示在K>3.3的信号呈现出一定的周期性，可以认定为是成周期变化的故障信号

其实随着N值的不断增加，即代表峭度计算包含的数据越来越多，可能会包含声发射信号同时也包含噪声信号，如果数据的额定时间跨度过大就很可能掩盖掉一些重要信息，这样就失去了峭度值计算的意义；但是如果时间差过于小，就会使信息量变得很小，无法达到对声发射信号的突出，以及对噪声信号的抑制效果。所以对于N值的选取应适当且谨慎[8]。

2 等时差峭度值计算

上文应用的峭度值分析方法是对固定个数的原始信号数据进行计算，但是在实际应用中很可能会出现两个原始信号之间的时间间隔比较长，则有可能导致峭度计算的数据时间跨度太大，掩盖了很多重要的信息。所以本文对传统的峭度分析进行了改进，设计了等时差峭度值分析方法。

等时差峭度值指在固定时间间隔T内对数据进行峭度计算，数据的个数不确定，这样很容易凸现信号的周期特性。波形图像如图2.1所示。

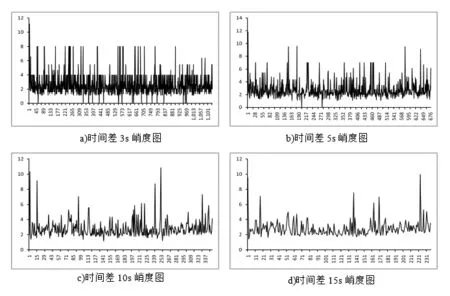
图2.1 等时差峭度值对比图

在等时差的峭度值计算中，效果相对还是比较明显的，与传统的峭度值计算的效果相比，K>3.3的信号峰值更加明显，所以在声发射检测中峭度的计算应用防范且效果明显。

峭度值分析能够有效的检测到实验条件下由于缺陷产生的声发射信号特征，为在噪声环境中检测声发射信号提出了有效的方法。

3 结论

从声发射信号的特征参数的特点出发，通过对特征参数的分析达到对声发射源的识别。由于声发射信号在采集过程中避免不了会有噪音信号的干扰，所以利用峭度分析，对声发射数据中的特征参数进行分析，突变现货偶可以得到进一步凸显，而噪声信号会被不断的抑制。通过这种方法，对数据中的特征数据进行区别采集，这些数据中基本包含着损伤的声发射信号，根据实际的应用创建了等差峭度和等时峭度两种峭度分析，并以图像的方式进行显示，进而可以通过这些数据对被检测材料的损伤进行定量和定性的分析。

[1]郝如江等.能量因子用于轴承故障声发射信号的特征提取[C].第十二届全国设备故障诊断学术会议论文集,2010.

[2]吴璞,夏长林.分段峭度值用于列车滚动轴承故障声发射诊断研究[J].机电产品开发与创新,2015,28(6):58-60.

[3]杨瑞峰,马铁华.声发射技术研究及应用发展[J].中北大学学报,2006,27(5):456-461.

[4]谢爱平,龚文,黄文学.声发射检测滑动轴承故障研究进展[J].湖南电力,2008(5):60-62.

[5]柏木万博.机械振动讲演文集[M].郑州机械研究所,1984:10-12.

[6]亢景福.混凝土硫酸盐侵蚀研究中的几个问题[J].混凝土,1995(3):9-18.

[7]赵洪波.声发射检测技术研究现状与发展方向[J].电子世界,2014,21(3):193-194.

[8]梁家慧.声发射仪器的进展[J].无损检测,2002,20(10):285-291.