基于模糊阈值的小波函数去噪算法

黎道花，周 骅

（贵州大学大数据与信息工程学院，贵阳 550025）

1 引言

小波变换在图像处理、压缩和小波去噪等领域应用十分广泛，但由于不同频率的时域选取的复杂性，尤其是由于噪声的存在，使分析变得困难[1-4]。通过将时域与频域两个空间单独分析，会发现噪声信号往往出现在高频段内。通过低通滤波器能够成功过滤高频段的噪声信号从而达到去除噪声的效果。小波包信号去噪主要包括确定分解层、选择小波包基、量化重构小波系数等步骤[5]。由于分解层、小波包基和阈值的选择比较困难，使其在实际应用中受到限制。近年来，众多研究者对此类问题做出研究，如文献[6]提出一种自适应小波去噪，设置合适的调整参数达到去噪的目的。文献[7]提出一种新颖的改进符号函数的小波阈值图像去噪系数，设置不同的调节因子分析图像中的信噪比变化。文献[8]提出一种改进的阈值函数，利用调节参数对典型的硬阈值和软阈值进行自适应调节，其峰值信噪比得到一定程度的改善。

本研究提出的改进算法，便是综合参考此类现有研究成果，利用硬阈值、软阈值两方面的优点，动态地选取阈值，以在图像处理中得到更加理想的去噪效果。

2 小波变换原理

在小波函数分析中，小波类型主要分为两类，即DB小波和Harr小波，分别侧重于对图形概貌和图形细节的分析，其双尺度方程如下：

式中，n=0,1,2,…。u0(t)则对应正交小波的尺度函数，u1(t)对应小波函数。hk和gk是利用正交小波基的滤波函数。图像中的混合信号为：

式中，s(t)为正交信号，η(t)为噪声。通过正交小波包变换，可得各分解层的逼近系数和细节系数。小波包算法通过频带的多尺度分解，可以对高频部分进行重分解，并对某一层小波信号进行重构。

常用阈值函数主要有硬阈值法和软阈值法，如Stein无偏的似然估计准则、最大最小阈值、固定阈值和启发式阈值等[9-11]。阈值的选取直接关系到去噪的效果，阈值选择偏大，会导致图像细节系数在跳变过程中出现损失或数据包丢失；阈值选取偏小，去噪效果则不明显，甚至小到近似于连续，没有跳变过程。目前经常使用Donoho等人基于高斯噪声模型的去噪法，它是基于独立正态遍历的决策理论提出的[12]，表达式为:

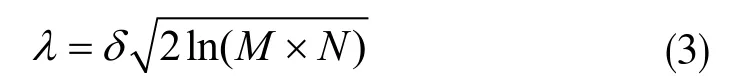
式中，λ为阈值，M×N是图像的像素，δ为高斯噪声的方差。

3 改进的模糊阈值算法

现有的小波阈值函数利用高斯噪声模型进行去噪，是基于独立正态遍历决策理论提出的。它在实际中的噪声无法预知，并且噪声会均匀地存在于信号的频带上。针对这一缺陷，对高斯噪声进行改进，得到一种模糊噪声模型，其表达式为：

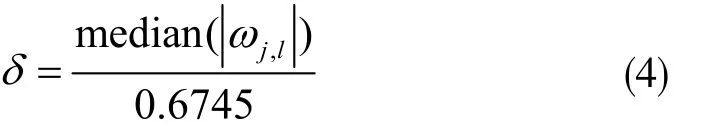
由此可得出新的阈值函数表达式为：

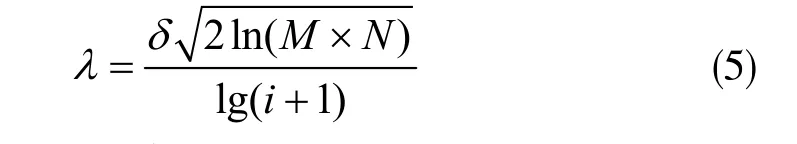
这里，方程中存在了lg(i+1)项，随着i的增大，阈值函数λ将会降低。小于λ的模糊系数最有可能由噪声产生，而大于λ的模糊系数最有可能由原始信号产生。

考虑到硬阈值的阈值函数是不连续的，软阈值具有常偏差，在此基础上对模糊阈值公式做出改进，取代了硬阈值和软阈值两个表达方法，直接合并成一个式子来表达。这也体现出了改进模糊阈值后的自适应性质。同时，通过改进模糊阈值函数而言，整个传输过程中的噪声也会变得越来越小，控制因子也会随着i值的增加，使阈值函数逐渐变小。

阈值函数中的细节系数包含更多的噪声，相关函数能够判断噪声背景中的有用信息，因此采用相关分析进行细节系数分析。改进模糊阈值的小波阈值算法的设计流程如图1所示。

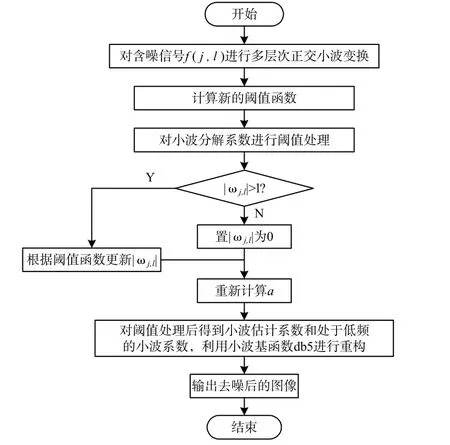
图1 改进模糊阈值小波去噪算法流程图

4 实验及结果分析

为验证改进模糊阈值的小波函数在图像处理中的有效性和实用性，以高斯白噪声下的Lorenz信号为实验研究对象。正交小波包具有消失矩序和支持集，前者决定了信号的接近能力，当阶数越大，分频效果越好，然而同时也会增加后者的长度和计算量。综合考虑算法的效果与效率，以db5小波为例进行分析。所有实验都基于MATLAB 2018a版本上的小波工具箱实现，小波基的分解层数为三层。

先在Lorenz数据中分别加入5%、10%、20%、30%、50%、70%和90%的高斯白噪声，然后使用db5小波包对污染信号进行分析。以不同噪声水平下的SNR和RMSE作为指标，对比情况如表1。

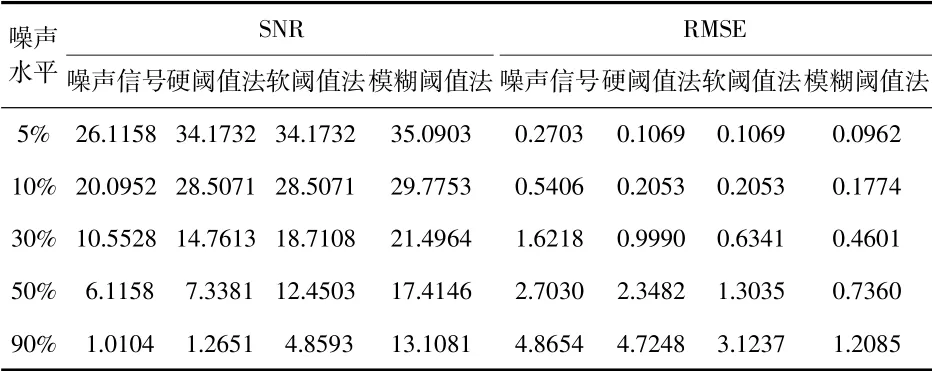
表1 不同噪声水平下各算法评价指标对比

由表中可见，改进的模糊阈值小波函数具有更好的信噪比，能获得更好的去噪效果。随着噪声水平的逐步增加，SNR会持续降低，但模糊阈值法与其他算法相比仍然具备良好的去噪性能。另外，从RMSE方面来看，模糊阈值去噪法的均方根误差相对更小，去噪效果更趋稳定。

实验对上述指标做了进一步的验证。对不同类型的系数采用奇异值分析、模糊阈值分析和相关性分析。结果表明，改进算法具有广泛的适用性，对不同噪声水平的信号去噪都是有效的。噪声水平越高，该算法去噪效果越好。实验条件选取噪声水平20%，得到信号去噪前后的相空间图和时间序列曲线，以反映不同改进阈值下的小波信号和噪声情况，实验结果如图2所示。

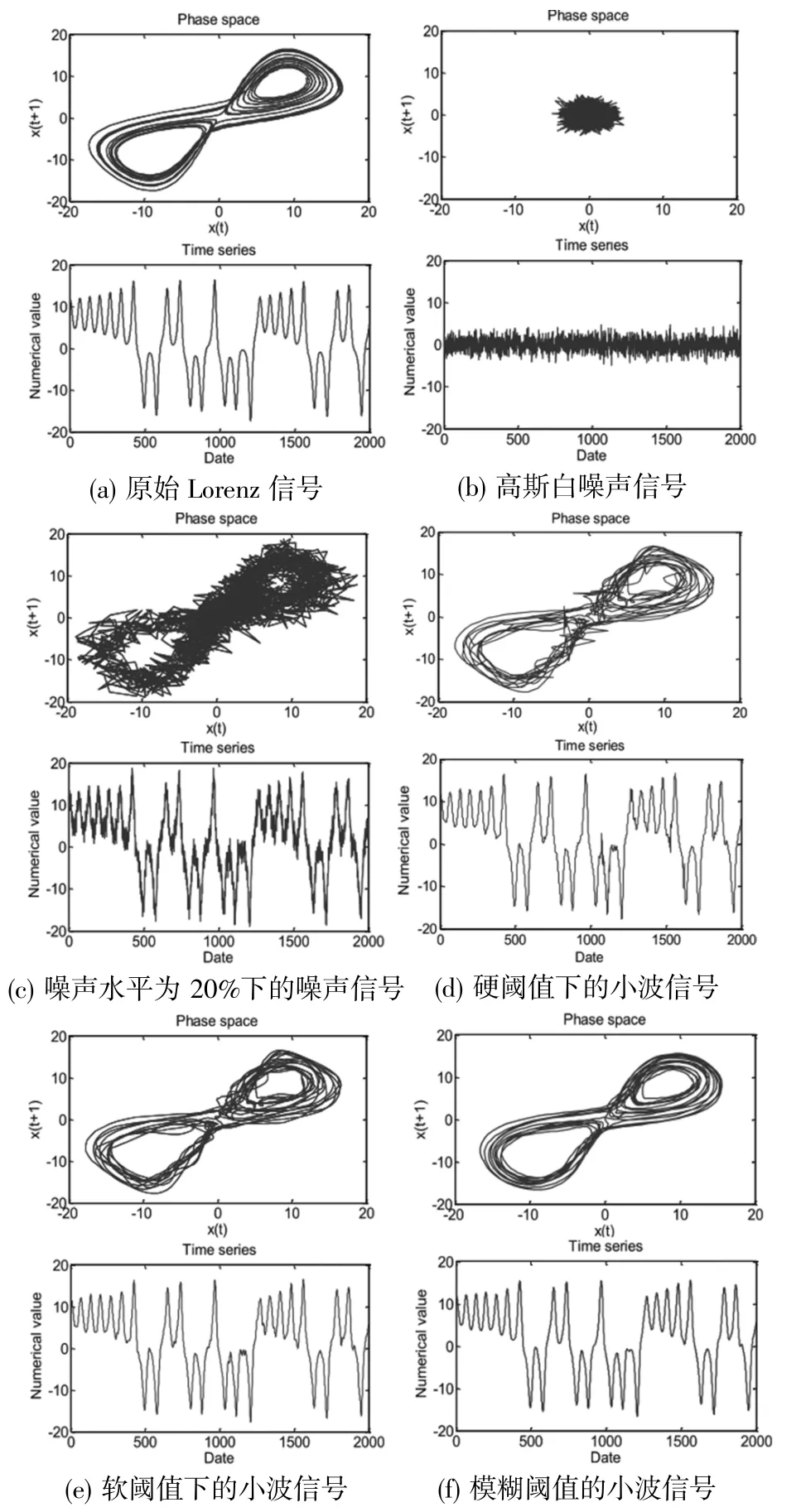
图2 不同改进阈值的小波信号和噪声

图中，经过小波包硬阈值和软阈值后的信号相空间图都比较粗糙，部分点偏离了原始轨迹。同时，时间序列曲线在某些地方存在振荡现象。这主要是由于选择了固定阈值。相比之下，改进算法不存在这种现象，能更好地反映系统的动态和平滑特性。

为进一步验证相关系数之间的评价方法，从相关系数方面进行实验分析，同样引入硬阈值和软阈值法的噪声信号进行实验对比。在给定延迟时间下，得出信号去噪前后的相关系数和相对偏差，实验结果如表2。

表2 不同噪声水平下的相关系数对比

通过表中数据对比可知，改进算法去噪信号的相关系数均为高相关。当噪声水平为70%时，与小波包硬阈值的相关性显著；当噪声水平为90%时，与小波包软阈值的相关性显著。改进算法的相对偏差也控制在很小的程度，小于0.5%。经过改进算法去噪的信号更接近原始信号的特征，实验中使用该算法对具体图像进行处理，处理效果如图3所示。

图3 不同去噪方法实验效果对比

从图中对比结果可清晰看出，改进的模糊阈值去噪法具有显著优势，体现出此方法在图像处理中的优越性。

5 结束语

改进的模糊阈值去噪算法改善了实际受噪声影响的信号特性。算法将小波包与奇异性、模糊阈值和相关性的分析结合起来，确定了最优改良方案。通过计算信噪比、均方根误差、相关系数和功率谱等不同去噪指标，反映出改进去噪算法的优缺点。经实验验证，新的算法不仅可以有效降低混沌噪声，对于具体图形所做的优化处理，该法也获得了更为显著的效果提升，因此具有一定的应用前景。