高考数学命题中结构不良预测题的思考

浙江 余继光

(作者单位：浙江省柯桥中学)

笔者以高中数学新教材为基础，以高考数学命题专家课题研究结论为依据，以经典数学模型为蓝本，创作高考数学命题立体几何、圆锥曲线、函数与导数结构不良预测题，为考生精心准备一首“交响曲”，让参加2022年高考的学子亲自“弹奏”一下，体验它的韵律.

结构不良数学试题具有选择性、探究性，学生能综合运用所学数学知识，进行探究，分析并最终解决问题，有些结构不良题条件封闭，需要创新结论；有些结构不良题结论封闭，条件可以创新；有些条件结论都封闭，求解策略开放的结构不良试题,但限于限时测评，目前高考数学命题给出若干个条件供考生选择，随着新高考数学命题改革的步步深入，在学生数学学习心理的承受范围内，在评价操作技术科学化发展后，开放程度更大的数学题也会在高考数学命题中出现.

1.立体几何

1.1 试题

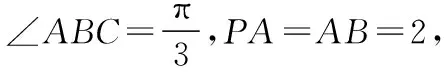
(1)若G为PC中点，求BG与平面PAB所成角的正弦值；

(2)从下面两个选项中任选一个探究

②在PC上是否存在一点H，使得AH⊥PD？

1.2 解析

(1)解法一：逻辑推理法

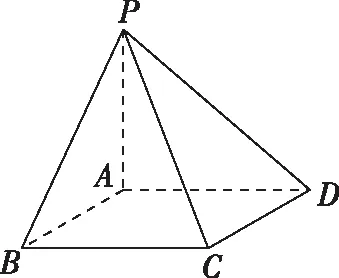
若G为PC中点，求BG与平面PAB所成角的正弦值，

如图，过G作GF垂直平面PAB于点F，连接BF，

则∠GBF为BG与平面PAB所成角，

由VG-PAB=VB-PAG，即

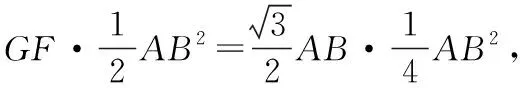
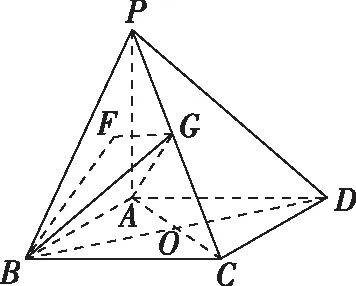
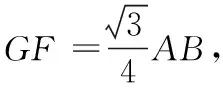
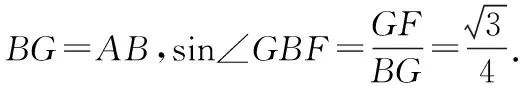
解法二：空间坐标法

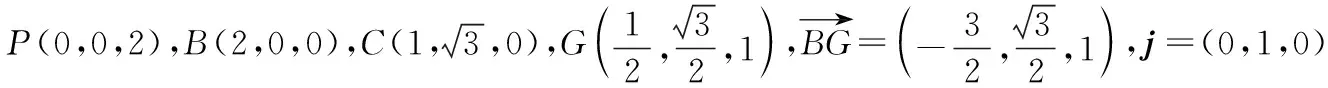
(2)解法一：逻辑推理法

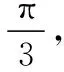
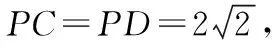
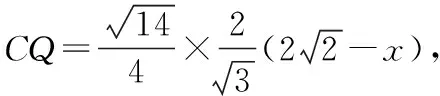
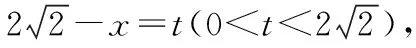
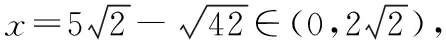
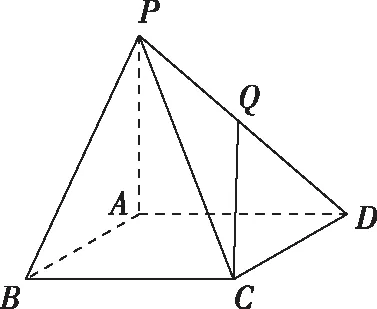
图1

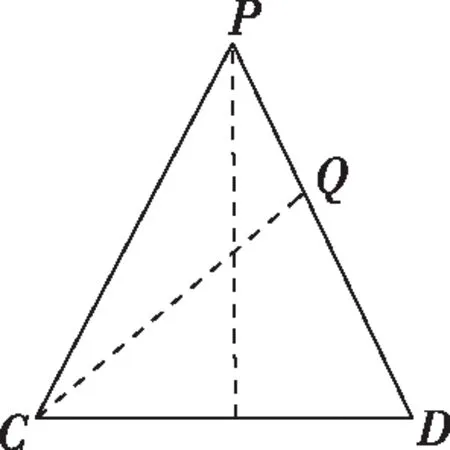
图2

②假设在PC上存在一点H，使得AH⊥PD，

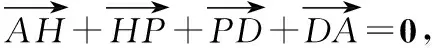
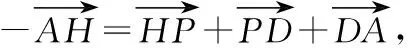
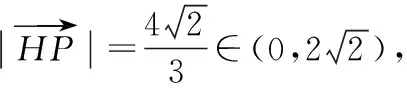
所以符合题意的点H存在.

解法二：空间坐标法

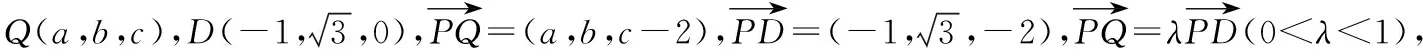
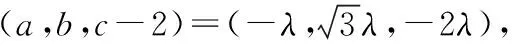
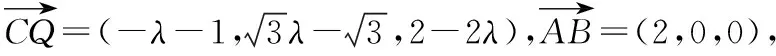
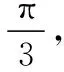
即(2λ+2)2=(λ+1)2+3(λ-1)2+(2-2λ)2，

即λ2-5λ+1=0，

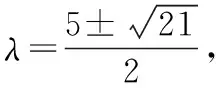
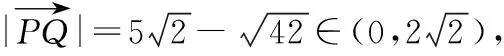
因此符合题意的点Q存在.

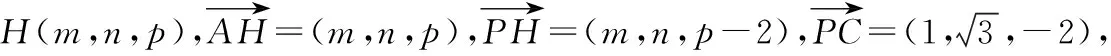
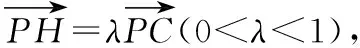
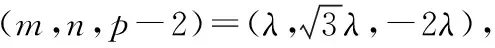
所以符合题意的点H存在.

1.3 命题依据

新高考数学立体几何命题进入规范几何图形时期，以三棱锥与四棱锥为主要背景成为常态，探究直线与直线、直线与平面、平面与平面的位置关系与度量关系，并且提供的选择性比较广泛，传统逻辑推理与空间坐标法均可使用，设计与数学新课标和新教材教学理念吻合的命题，尤其是突出探究性与创新性，以上预测题依据《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课程标准》)评价水平二：“能够在关联的情境中，想象并构建相应的几何图形；能够借助图形提出数学问题，发现图形与图形、图形与数量的关系，探索图形的运动规律；能够掌握研究图形与图形、图形与数量之间关系的基本方法；能够借助图形性质探索数学规律，解决实际问题或数学问题；能够通过直观想象提出数学问题；能够用图形探索解决问题的思路；能够形成数形结合的思想，体会几何直观的作用和意义；在交流的过程中，能够利用直观想象探讨数学问题.”

2.解析几何

2.1 试题

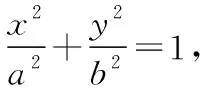
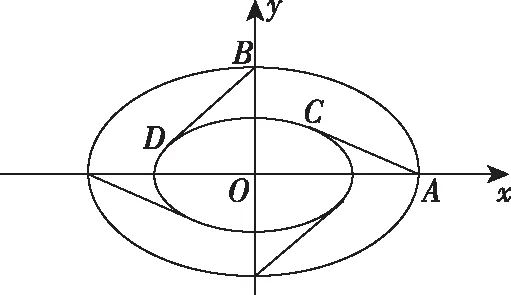
(1)求椭圆的离心率；

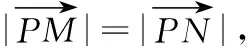
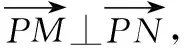
求x0的值.

2.2 解析

(1)解法一：A(na，0)，B(0，nb)，设切线AC的方程为y=k1(x-na)，切线BD的方程为y-nb=k2x，于是由

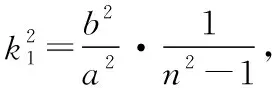
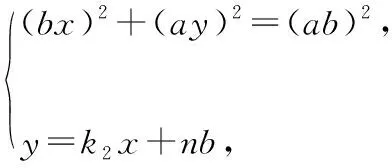
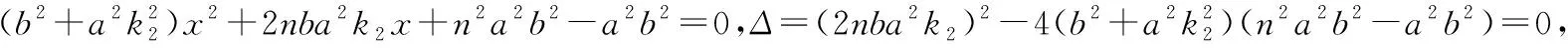
解法二：设C(x1,y1)，D(x2,y2)，

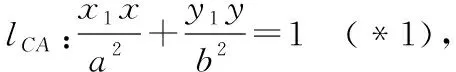
把A点代入(*1)，B点代入(*2)得

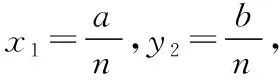
解得a2=12，b2=4，

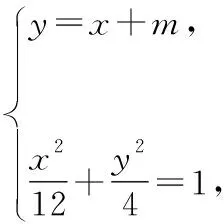
因为直线l与内层椭圆交于不同两点M,N，

所以Δ=36m2-16(3m2-12)>0，得m2<16.

设M(x1,y1),N(x2,y2)，则x1，x2是方程(*)的两根，

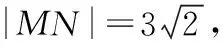
据题意知，点P为线段MN的中垂线与直线y=2的交点.

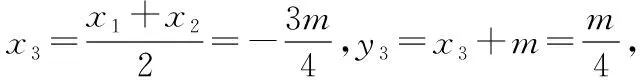
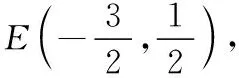
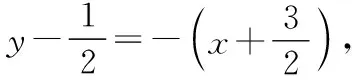
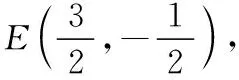
即y=-x+1.令y=2，得x0=-1.

综上所述，x0的值为-3或-1.

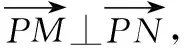
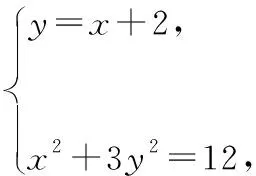
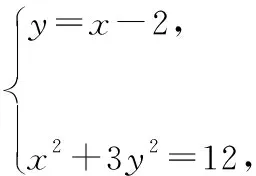
综上所述，x0的值为-3或3.

2.3 命题依据

新高考数学命题在检测学生数学核心素养的同时，突出教育功能，承载数学文化，2022年是冬奥之年，冬奥开幕式的一片雪花在鸟巢上演，带给全世界一个惊喜，以鸟巢为现实情境创作数学问题是一次命题创新实践，以上预测题依据《课程标准》水平二：“能够在关联的情境中确定运算对象，提出运算问题；能够针对运算问题，合理选择运算方法、设计运算程序，解决问题；能够理解运算是一种演绎推理；能够在综合利用运算方法解决问题的过程中，体会程序思想的意义和作用.”

3.函数导数

3.1 试题

已知f(x)=ax3-ex，e=2.718 28…为自然对数的底数.

(1)若f(x)是R上的单调函数，求实数a的取值范围；

(2)当a<0时，从下面两个选项中任选一个

①对任意x≥0；

②对任意实数x.

试问函数f(x)是否存在最大值？若存在，求出函数f(x)的最大值，若不存在，说明理由；

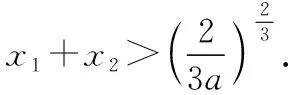
3.2 解析

(1)f(x)=ax3-ex，f′(x)=3ax2-ex，

当a=0时，f(x)在R上单调递减；

当a<0时，f′(x)<0，f(x)在R上单调递减；

当a>0时，f′(x)的正负不定，此时f(x)在R上不单调，

综上，实数a的取值范围是(-∞，0].

(2)由(1)知，当a<0时，f(x)在R上单调递减，

①对任意x≥0，f(x)≤f(0)，而f(0)=-1，

所以f(x)≤-1，

故当x=0时，f(x)取得最大值-1，

所以函数f(x)存在最大值，且最大值为-1.

②对任意实数x∈R，由(1)知，当a<0时，f(x)在R上单调递减，所以f(x)取不到最大值，因此f(x)不存在最大值.

(3)当a>1时，由f(x)有两个正极值点x1，x2，

则x1，x2是方程f′(x)=3ax2-ex=0的两个根，

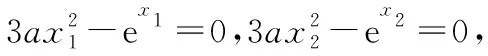
所以9a2(x1x2)2=ex1+x2≥1+x1+x2>x1+x2，

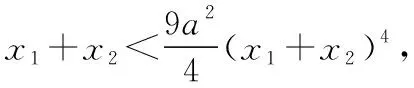
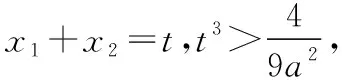
3.3 命题依据

函数与导数结构不良题命题主方向预测是零点的综合问题，关键是分析超越函数、参数范围、函数性质之间的关系，教学中可以分层设计同一情境的不同层次、不同难度的题目，训练学生的数学思维，2021年是如此，2022年仍将如此.以上预测题依据《课程标准》评价水平二：“能够在关联的情境中，发现并提出数学问题，用数学语言予以表达；能够理解、归纳、类比是发现和提出数学命题的重要途径；能够对与学过的知识有关联的数学命题，通过对其条件与结论的分析，探索论证的思路，选择合适的论证方法予以证明，并能用准确的数学语言表述论证过程；能够通过举反例说明某些数学结论不成立；能够理解相关概念、命题、定理之间的逻辑关系，初步建立网状的知识结构.”

高考数学结构不良问题类型很多，可以预见新高考数学命题会不断延伸，因为只有这样，才能真正培养学生的创新意识与创造能力.

数学结构不良题解题与教学口诀：

提出问题合题意，探究意识要建立，选择问题需谨慎，推理严密表达全，多向思考是基础，结构不良需完善，有限开放是常态，无限视角是落点.