基于直观想象的立体几何试题命制探究

福建 林清利 唐碧容

(作者单位：福建省莆田第一中学)

2020-2021年的高考试题全面考查了高中数学六大核心素养，作为一线教师应当充分挖掘高考试题的内涵，领会核心素养导向，并潜心探索如何在平时的课堂中加以落实.直观想象是六大核心素养之一，它是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.通过直观想象，可以预判问题的发展方向，站在更高的角度俯瞰题目，抓住问题的核心，命制万变不离其宗的试题.

本文通过一道高考真题的变式研究及溯源，以一题多解、一题多变、回归教材等方式研究问题本质.先用解析法探究，然后着重用几何法分析，通过直观想象感知空间中的线面角、二面角的作图方法，减少计算量，提高抽象思维的要求.阐明变式过程中的“变”与“不变”，抓住变式规律和方向，形成命题式的教学模式，并以“微专题”的形式在平时教学中加以实践.

1.经典母题

【例】(2021·全国甲卷理·19)已知直三棱柱ABC-A1B1C1中，侧面AA1B1B为正方形，AB=BC=2，E，F分别为AC和CC1的中点，D为棱A1B1上的点，BF⊥A1B1.

(1)证明：BF⊥DE；(2)当B1D为何值时，平面BB1C1C与平面DFE所成的二面角的正弦值最小？

分析：本题的几何体是直三棱柱,这给考生直观的视觉感知.题干中第二个条件蕴含垂直,结合最后一个条件,先直观预判BA,BC,BB1两两垂直,然后借助长度关系加以证明，这坚定了考生建立直角坐标系来解题的自信.

虽然D是动点,造成两个问题中均含有动态的直线或平面的空间角的问题,但是命题人把动点D控制在直线A1B1上,使用坐标法可以简洁轻松地完成本题两问,一气呵成.

2.解题探究

若仅满足于坐标法解题,便缺少对本题命制手法的探究.基于直观想象的几何法无疑是探究本题的最佳视角,下面探究本题的特点、解法、题源及变式.

第(1)问分析1:注意到DE始终在△A1B1E内,故只需证明BF⊥平面A1B1E.

第(1)问分析2:考虑到BF是在“竖直”的平面B1BCC1内,而DE不在平面B1BCC1内,故只需证明DE在平面B1BCC1的投影与BF垂直即可.

第(2)问图中没有平面BB1C1C与平面DFE的公共棱,故应先把平面DFE延展,进而作出公共棱.

解答：(1)略；(2)如图1,延长EF,A1C1,设EF∩A1C1=G,连接DG,设DG∩B1C1=H,连接FH.

图1

思路一:从点D出发作平面角.

解法一：如图2,过B1作B1J⊥FH,垂足为J,连接DJ.由(1)知A1B1⊥平面B1BCC1,则A1B1⊥FH,且A1B1∩B1J=B1,从而FH⊥平面B1DJ,那么DJ⊥FH,所以∠B1JD是二面角D-FH-B1的平面角.

此时sin∠B1JD也最小.

图2

思路二:从点E出发作平面角.

那么当C1H=n=1时tan∠ELK最小,

图3

思路三:注意到△DEF在平面B1BCC1内的投影是确定的三角形,故无需作出公共棱和平面角.

解法三：如图4,设BC中点为K,连接EK,KB1,B1F,FK,易证EK⊥平面B1BCC1,则△DEF在平面BB1C1C内的投影为△B1FK.设所求角为θ,△DEF与△B1FK的面积分别记为S△DEF,S△B1FK,

则S△B1FK=S△DEF·cosθ,由于EF,S△B1FK为定值,故当cosθ最大时,S△DEF最小,

从而点D到直线EF的距离最小,其最小值为异面直线A1B1与EF之间的距离d.

又由于A1B1∥平面EFK,那么d等于A1B1到平面EFK的距离,

即d等于B1到平面EFK的距离,亦即d等于B1到FK的距离.

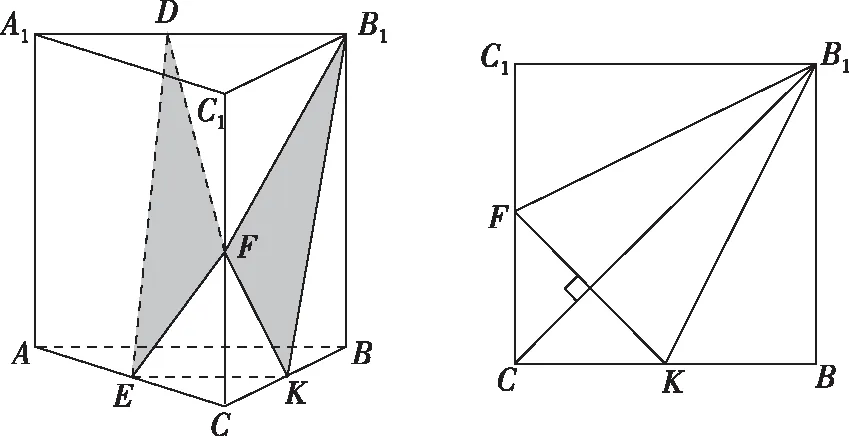
图4

如图5,连接B1C,CA1,设EF∩A1C=M,易知点M是线段A1C的三等分点(靠近C)，

又EF⊥B1C,A1B1⊥B1C,那么当DM∥B1C时,DM为异面直线A1B1与EF的公垂线.

从而点D是线段A1B1的三等分点(靠近B1),

图5

以上三种解法虽然都是几何法,但是在计算量、思维量上有较大差别.解法一中由于D是动点,导致△B1DJ三边均是变化的,计算量大;解法二中E是定点,Rt△ELK的一条直角边是固定的,从而在计算量上得到了较大的精简;解法三站在结论的基础上看问题,并不断地转化问题,几乎没有运算量,把动态问题“动中求静”的思路发挥得淋漓尽致,直击问题本质.

3.变式拓展

母题变式1：尺规作图问题在全国卷考题中也经常涉及,特别截面问题是热点、难点问题.本题中△DEF在几何体内部,故可在本题中增加一问：“请作出平面DFE截三棱柱ABC-A1B1C1的截面.”

解：延长EF,A1C1,设EF∩A1C1=G,连接DG,设DG∩B1C1=H,连接FH,则四边形DEFH为所求截面.

母题变式2：由解法二发现点H完全由点D控制,且平面BB1C1C与平面DFE所成二面角的正弦值最小时,点H恰为线段B1C1中点,故本题可以改编为“H为棱B1C1上的点,当平面BB1C1C与平面EFH所成二面角的正弦值最小时,请确定点H的位置.(其他条件不变)”这样设计从结果上看是中点,数据更直观,更具有对称美.

简解：由上面的解法二可知当H为B1C1中点时,所求二面角的正弦值最小.

母题变式3：改变目标函数,例如求DE与面BB1C1C所成角的正弦值的取值范围.

简解：作DE在平面BB1C1C内的投影为B1K,DE与平面BB1C1C所成角α,则0≤α≤∠EB1K,

4.题源探究

1.如图,两条异面直线a,b所成角为θ,在直线a,b上分别取点A′,E和A,F,使AA′⊥a,且AA′⊥b,已知A′E=m,AF=n,EF=l,求线段AA′的长.

2.(2013·北京卷理·14)如图，在棱长为2的正方体ABCD-A1B1C1D1中，E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为________.

评注：以上两题实质是探究两条异面直线间的距离.虽然教材中不提这个概念,但是仍然作为习题探究.而且一些考题中会蕴含该模型,值得关注.

(1)证明：PO⊥平面ABC；

(2)若点M在棱BC上，且二面角M-PA-C为30°，求PC与平面PAM所成角的正弦值.

分析：第(2)问注意到二面角M-PA-C的一个半平面和所求问题中的平面PAM是公共的,而直线PC恰在另一个半平面内,从而本题非常适合从定义出发,借助投影,运用几何法可以避开求解点M的坐标,也无需确定点M的准确位置,从而快速破解.

解：(1)略;(2)设AP中点为Q,连接CQ,则CQ⊥AP,作QN⊥AP交PM于N,则∠CQN=30°,

4.(2020·新高考Ⅰ卷·20)如图，四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.

(1)证明：l⊥平面PDC；

(2)已知PD=AD=1，Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.

分析：由条件可知DA,DC,DP两两垂直且长度均相等,从而可以把几何体补形为正方体,这样直线PB在平面QCD的投影就比较直观,从而可以快速破解.

评注：以上两道高考题以正方体为载体或有面面垂直等特殊条件,利用这样的几何直观解题简洁大气,令人回味无穷,惊叹模型的魅力,可以感受到全国卷命题专家的深厚功力.

5.总结规律

从上述考题的特点与解法中可以发现高考命题的一个基本理念是让学生“多思少算”,那么要如何正确地思考,发散地思考呢?答案是基于核心素养的思考.利用几何直观,充分发挥想象,把解题与命题关联起来,真正实现从解题到解决问题的升华.

对于立体几何试题的解题与命制,对学生与教师的建议如下:

1.对于学生

(1)重视基本概念.概念是一切问题的基础,数学玩得就是一个概念.学生在学习与复习的过程中要高度重视教材中关于概念的生成、理解和应用；

(2)重视基本方法.立体几何中有坐标法与几何法两个基本方法.两者要并重,特别是在解答题中,不能只会坐标法,适当地使用几何法探究,将会收获更多的思路与解法.

2.对于教师

(1)重视教材.一方面，钻研教材,熟悉教材,才能整体把握知识的系统性.另一方面,高考试题的基本素材是教材.教材中的概念辨析,习题改编等都要高度重视；

(2)探究解法与变式.作为教师不能仅满足坐标法,更需要熟悉几何法.把问题归类、模型化,探究其本源,进而把问题变式,实现多题一解,再尝试命制一些试题,提升自身的综合素质.

6.结束语

基于直观想象的立体几何试题的命制，首先要明确考查目标，然后寻找合适典型的模型载体，揭示问题本质，最后控制变量，明确问题中“变”与“不变”的关系,从解析法和几何法的角度分别解释“变”与“不变”.新高考试题正往兼具选拔和育人功能的良性方向不断发展，作为一线教师，我们也要全力配合，我们的数学教学也应该是以育人为导向，课堂中要给学生发现问题、探究问题、讨论问题、解决问题、改变问题的命题式数学学习体验，提高他们直观感知、预测、论证数学问题的能力.

(本文为福建省教育科学“十四五”规划2021年度专项课题《核心素养视域下高考数学命题研究》研究成果之一(课题编号Fjjgzx21-006)