追本溯源 高瞻远瞩——立体几何中的动态问题研究

浙江

(作者单位：浙江省柯桥中学)

立体几何中的动态问题，其核心考点是动点和动直线所构成的静态平面，难点是考查学生数学核心素养和创新思维能力，已成为新高考命题的一大热点.深挖其问题背景，总结其求解方法，掌握其证明技巧，透析其变化规律，对提升考生的数学复习效益将大有裨益.

一、真题研学

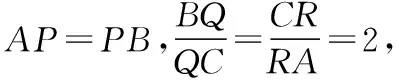
A.γ<α<βB.α<γ<β

C.α<β<γD.β<γ<α

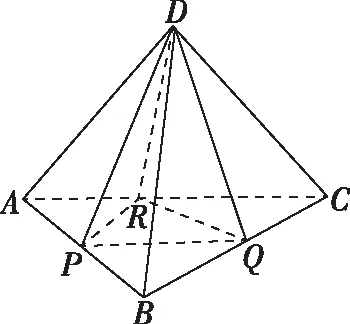
根据题意，过D作平面ABC的高DH，过H分别作PR,PQ,QR的高HE,HF,HG，如图，易得α=∠DEH，β=∠DFH，γ=∠DGH，可以看出它们的对边都是一样的，所以只需要比较EH,FH,GH三边的大小即可，即把立体问题转化为底面平面几何问题.

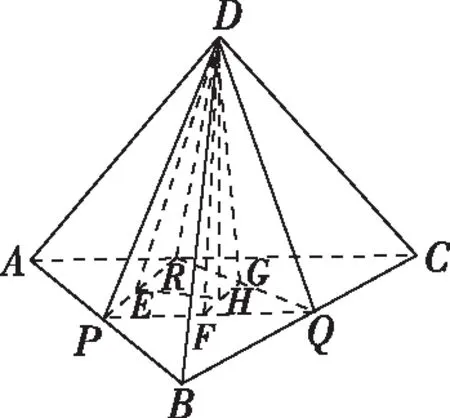
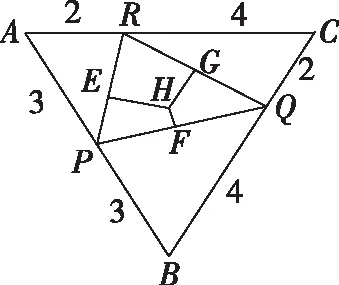
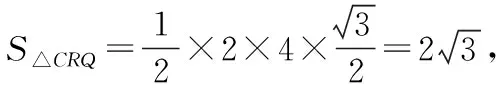
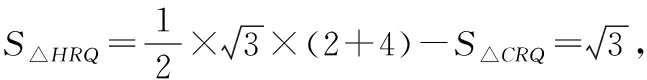
然后我们细究命题思路，该题是在取底面正三角形三边中点的基本模型下，改为其中两边的近、远三等分点，从而命制出一个立足课本基本模型的立体几何好题，我们就以该真题为研究对象，将中点、三等分点改成任意棱上一点，编制出一道一模题如下.

二、好题细品

母题：如图，三棱锥V-ABC的底面ABC是正三角形，侧棱长均相等，P是棱VA上的点(不含端点)，记直线PB与直线AC所成角为α，二面角P-AC-B的平面角为β，则α+β不可能是( )

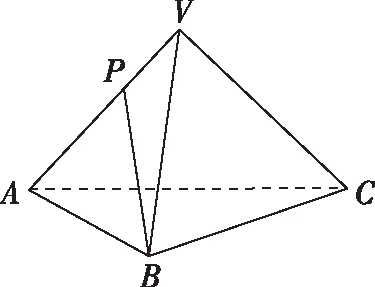
点评：该题是将极限思想运用到立体几何中，将三棱锥趋向于无穷小及无穷大，则角的范围迎刃而解.

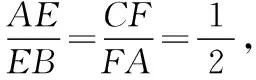
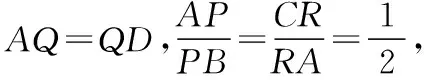
A.β>γ>αB.α>β>γ

C.α>γ>βD.β>α>γ

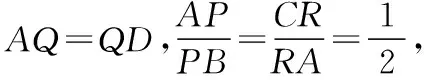
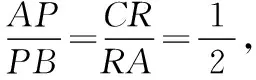
继2017年之后，浙江卷2018，2019两年连续考到了动态空间三角的大小比较关系，通法是通过线面垂直关系先做出线线、线面、二面角，把立体几何问题最终转化为一个简单平面问题，再比较线段长大小.当然空间三角大小关系也隐含着最小角，最大角定理的运用.

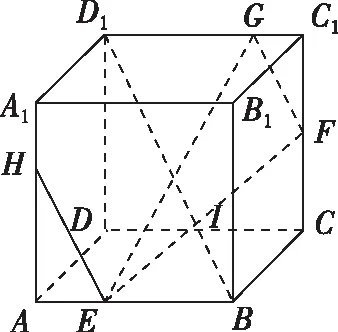
(2018·浙江卷·8)已知四棱锥S-ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点(不含端点),设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S-AB-C的平面角为θ3，则( )

A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1

C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1

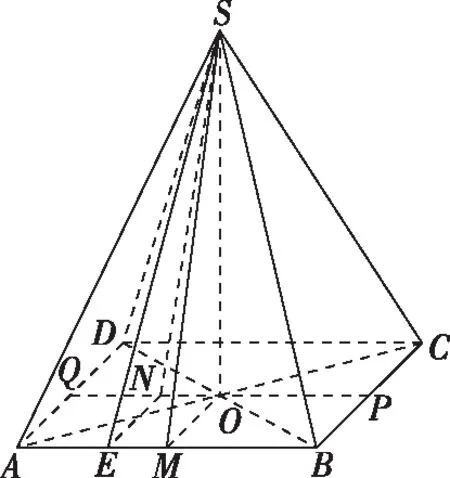
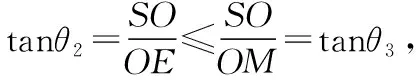
(2019·浙江卷·8)设三棱锥V-ABC的底面是正三角形，侧棱长均相等，P是棱VA上的点(不含端点).记直线PB与直线AC所成的角为α，直线PB与平面ABC所成的角为β，二面角P-AC-B的平面角为γ，则( )

A.β<γ，α<γB.β<α，β<γ

C.β<α，γ<αD.α<β，γ<β

2019年高考的动态立体几何仍延续2018年的最小角、最大角定理，故易选B.

然后我们将模型由三棱锥换成标准正交匀称图形正方体，设置一个由动点连接定点的隐平面，即得到以下题目.

【变式2】(2021·宁波一模·16)在正方体ABCD-A1B1C1D1中，E为线段AB上任意一点(不含端点)，F为CC1的中点，G为C1D1的四等分点(靠近点C1)，直线AA1交平面EFG于点H，则直线EH与直线BD1所成角的余弦值是________.

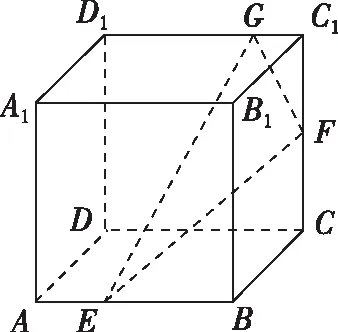
该题虽E为动态点，而事实上平面ABB1A1∥平面DCC1D1，平面EFG为截面，过E作EH∥FG交AA1于点H，平面EFG与平面ABB1A1和平面DCC1D1截得的两直线EH∥FG，从而直线EH与直线BD1所成角等于直线FG与直线BD1所成角.以下可使用向量的对角线定理

关于平面的延拓性是共面的难点，该知识点在2021年浙江卷第6题进行了考查.

如图，已知正方体ABCD-A1B1C1D1，M，N分别是A1D，D1B的中点，则( )

A.直线A1D与直线D1B垂直，直线MN∥平面ABCD

B.直线A1D与直线D1B平行，直线MN⊥平面BDD1B1

C.直线A1D与直线D1B相交，直线MN∥平面ABCD

D.直线A1D与直线D1B异面，直线MN⊥平面BDD1B1

需要将D1B固定到平面ABD1，连接AD1，由正方体可知A1D⊥AD1，A1D⊥AB，所以A1D⊥平面ABD1，A1D⊥D1B，易得MN∥AB，MN∥平面ABCD.所以A选项正确；由正方体可知A1D与平面BDD1相交于点D，D1B⊂平面BDD1，D∉D1B，直线A1D与直线D1B是异面直线，B，C错；因为MN∥AB，AB不与平面BDD1B1垂直，所以MN不与平面BDD1B1垂直，故D错，故选A.

通过以上三例我们阐述的是立体图形中的动点，动直线运动规律，而在新普通高中教科书数学必修第二册中，明确告诉我们什么是立体几何，立体几何是在平面几何的基础上构成的正交或是仿射维度图形，其本质是基于点射影的解析几何.鉴于此，2022年高考动态立体几何试题命制将青睐于平面几何的折叠，依照母题的三棱锥，改编成平面图形为三角形的翻折问题，得到变式3.

三、2022年真题预测

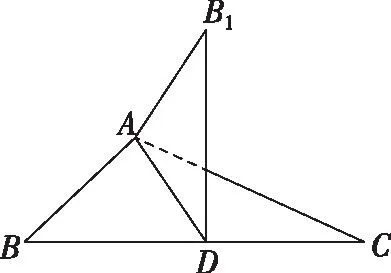
【变式3】如图，已知△ABC中，AC>AB,AD是∠BAC的平分线，将△ABD沿直线AD翻折成△ADB1,在翻折过程中，设所成二面角的平面角B1-AD-C为α，∠B1AC=β,∠B1DC=γ,则下列结论中成立的是( )

A.α≥β,α≥γB.α≥β,α≤γ

C.α≤β,α≥γD.α≤β,α≤γ

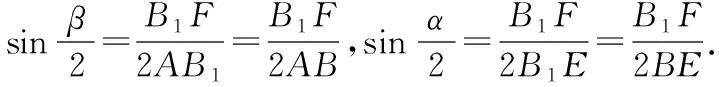
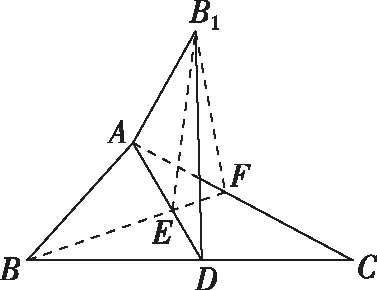
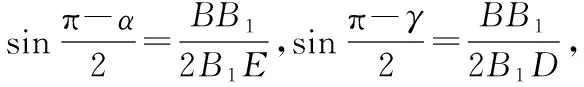
点评：立体几何翻折问题常先考虑折叠前图形与折叠过程中的图形的变量与不变量，也是极端法的缘由，其次该题解法的纽带是投影点B′一定落在AD的高线上.

当然在考场上，我们可以再次引入点的极限逼近思想，考虑两个极端位置，在初始位置，易知α=π,α>β,α=γ,其次在点B经过180°折平时易知α=β=0,α<γ，易得准确答案B，让我们再次感叹动态逼近思想的精妙绝伦.

此外我们也可以把基本图形改为直角三角形，在折叠过程中构成标准垂直的立体点正投影，得到试题变式4.

【变式4】在△ABC中，∠ACB=90°,BC=2,AC=3，点D在斜边AB上，以CD为棱把它折成直二面角A-CD-B，折叠后AB的最小值为( )

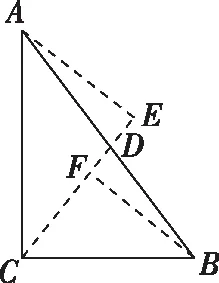
因为折成直二面角A-CD-B，为标准正投影，故点A的投影必在直线CF上，该题本质是两个直角三角形的标准墙角模型.简单计算下可设∠ACE=θ,AE=3sinθ,CE=3cosθ,CF=2sinθ,BF=2cosθ，所以AB2=13-6sin2θ≥7，故选B.变式3与变式4是笔者对2022年高考动态立体几何的预测.

四、结束语

《普通高中数学课程标准(2017版2020年修订)》指出“高中数学教学以发展学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质”.本文阐述的立体几何动态问题研究正是落实这一理念的良好载体.在解决此类题型时，教师要以高考真题为核心，从学生的角度去思考问题，从条件或是结论或是模型的演变为导向得到变式题型，由浅入深，由易到难，由特殊到一般，层层深入，步步启发.精心设计的变式题组在教学中发挥着不可替代的作用，对于提高教学效率、培养尖子生的能力、提高学生的数学素养起着重要作用，笔者鉴于此与各位读者共勉，希望能不断优化课堂教学，研讨出更多值得品味的优质试题.