例谈“三多”在共线向量与圆锥曲线交汇问题中的应用

河北 郭天总 王红波

(作者单位：邯郸市永年区第二中学)

新高考重视能力立意、情境命题，尤其是在知识网络的交汇点上设计试题，而平面向量与圆锥曲线结合的这类问题能有效的考查学生的数形结合思想、化归与转化思想、分析法与综合法等数学思想和方法，能加强高中数学知识各分支之间的联系，开拓解题视野，提高学生数学解题能力和水平.因此，圆锥曲线与平面向量的融合交汇是新课程高考命题改革的发展方向和创新的必然趋势.而学生对这部分内容普遍感到不适应.那么，在解析几何复习时,该如何融合平面向量的基础、渗透平面向量的基本方法提高复习效率呢？

笔者认为“一题多解”“一题多变”“多题一解”是一种高效的复习方法，“一题多解”即一道题有多种解法，该方式可以锻炼学生的发散思维，开阔学生的思路；“一题多变”即对一道题从问题情境、问题的方式等方面进行改变，达到触类旁通、举一反三的效果；“多题一解”即某类问题用的是一种解题思想或考查的是同一个知识点，该方式可以帮助学生归纳总结题型，避免题海战术，达到跳出题海的目的.总之，用“三多”的模式去复习，可以大大提高复习的效果，达到事半功倍的效果.

本文以共线向量与圆锥曲线交汇的问题为例，探析在复习中如何做到以上所说的“三多”，希望能起到抛砖引玉的作用.

一、母题探究

【分析】看问题：求直线l的斜率.

想方法：求直线斜率的基本方法：

(1)通性通法：属于求值问题，考查方程思想，找出等量关系建立关于直线l斜率的方程去求解.

定义法：k=tanα(α≠90°).

(2)过F的直线l交抛物线于A，B两点，由此可得：

①想坐标可知，A，B两点坐标满足抛物线及直线AB的方程；

②想定义可得，A，B两点到焦点F的距离等于到准线的距离；

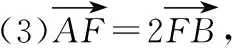
定措施：方法一：由①④可得A，B两点的坐标，故可用公式法求斜率；

方法二：由③④可知利用韦达定理建立直线l的斜率的方程去求斜率；

方法三：由③⑤可知能用定义法求斜率；

方法四：由②⑤可知能用定义法求斜率.

【解析】方法一：由题知p=1，则抛物线方程为y2=2x，设A(x1,y1)，B(x2,y2)，

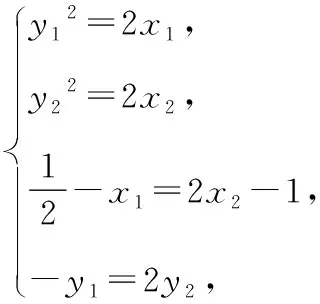
代入抛物线方程得y2-2my-1=0，设A(x1,y1)，B(x2,y2)，

由韦达定理得y1+y2=2m，y1y2=-1，

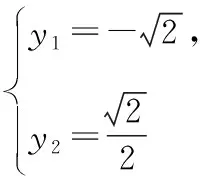
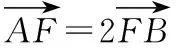
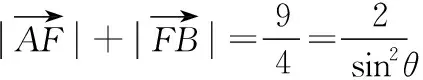
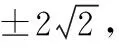
图1

图2

二、方法总结

上面通过“十二字分析法”，即“看问题、想方法、看条件、定措施”，对母题进行了分析，得到了四种解题方法，其中方法一、方法二属于通性通法，方法三利用了抛物线焦点弦的性质、方法四利用了抛物线的定义，都属于专题专法.

“十二字分析法”可以把解题的分析过程、思考过程完全展现给学生，真正做到授之以渔，使学生不但知其然而且知其所以然.“十二字分析法”也可以提高学生分析问题解决问题的能力，有利于培养学生的程序性思维，有利于培养学生一题多解的思维意识.但要想能够熟练地使用“十二字分析法”，需要学生对高中数学基本题型的解题方法熟记于心，比如求轨迹方程的基本方法有待定系数法、定义法、直译法、代入法(相关点法)、参数法.当遇到求轨迹方程的问题时，首先要想到这些基本方法，然后再分析条件，结合条件选择合适的方法去解决问题.如果基本方法没掌握，那做题时就会像无头苍蝇，没有明确的解题思路.

三、解题心得

在有关直线与圆锥曲线的问题中，几乎都有“点在圆锥曲线上”这样的一个条件，对于这个条件一般可以从两个角度去思考：一是想定义，即想圆锥曲线的定义；二是想坐标，即该点的坐标要既满足圆锥曲线的方程，也满足直线的方程.一般情况是选择填空题想定义，即利用定义去解题；解答题想坐标，即联立直线与圆锥曲线的方程再结合韦达定理去解题.在母题讲解中，方法一、方法二利用的是坐标，方法三用的是抛物线焦点弦的性质，方法四用的是定义.

在有关共线向量与圆锥曲线交汇的问题中，对于“共线向量”这一条件一般从两个角度去出发：一是想向量的模，即根据该条件得到已知向量模的关系，利用这一关系或利用向量模所隐藏的几何关系去解题；二是想坐标，即根据该条件得到已知两向量起点终点坐标的关系，再与韦达定理相结合去解题.

四、变式拓展

(一)以“变换问题情境”为指导思想进行变式

椭圆、抛物线、双曲线统称为圆锥曲线，它们有很多相似的几何性质，因此把三者进行互换，可达到改变问题情境的目的，以此进行一题多变，开展变式教学.

【分析】看问题：求直线AB的斜率k(属于求值问题).

想方法：求直线斜率的基本方法：

(1)通性通法：属于求值问题，考查方程思想，找出等量关系建立关于直线l的斜率的方程去求解.

定义法：k=tanα(α≠90°).

(2)过右焦点F的直线交椭圆C于A，B两点，设A(x1,y1)，B(x2,y2)，由此可得：

①想坐标可知，A，B两点坐标满足椭圆C及直线AB的方程；

②想椭圆的定义.

⑤想共线向量可知，A,F,B三点共线.

定措施：方法一：由①④结合韦达定理建立关于k的方程去求解；

方法二：由①④结合点在椭圆上关于k的方程去求解.

设A(x1,y1)，B(x2,y2)，

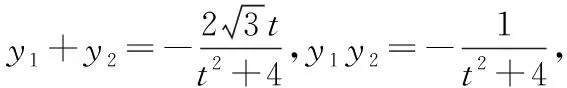
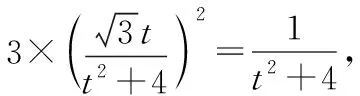
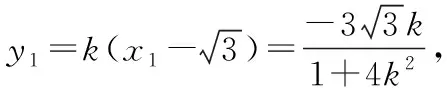
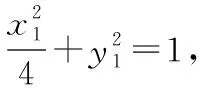
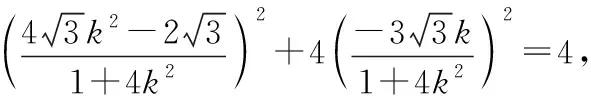
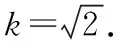
【分析】看问题：求a的值(属于求值问题).

想方法：求值问题考查方程思想，找出等量关系建立关于a的方程去求解.

①想坐标可知，A，B两点坐标满足双曲线C及直线AB的方程.

④想共线向量可知，A，P，B三点共线.

定措施：方法一：由①②结合韦达定理建立关于a的方程求解；

方法二：由①②结合点在双曲线上建立关于a的方程求解.

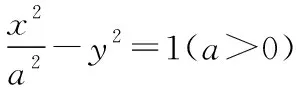
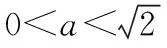
由于x1,x2是方程(1-a2)x2+2a2x-2a2=0的两根，且1-a2≠0，

方法二：设A(x1,y1)，B(x2,y2)，

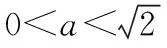
【点评】变式1是根据母题把抛物线改成了椭圆，但弦还是焦点弦，由于椭圆的焦点弦没有抛物线焦点弦类似的结论，所以只能从坐标的角度去解决问题；变式2是根据母题把抛物线改成了双曲线，弦也不是焦点弦了，也是从坐标的角度去解决问题，这也说明了用坐标法是解决共线向量与圆锥曲线问题的通性通法.

(二)以“变换所求量”为指导思想进行变式

A.2B.3C.4D.5

【答案】B

【答案】C

【答案】A

【点评】变式3，4，5是针对母题，通过改变所求量或曲线的方程得到的变式.希望读者可以自己尝试着用“十二字分析法”去探索这些变式的解法.变数据、变问法、变情境是进行一题多变的基本策略，尤其对于以共线向量与圆锥曲线为情境的交汇问题，可依据这三种策略进行一题多变，开展变式教学.

五、结语

以上的母题也好，变式也好，都是以共线向量与圆锥曲线为情境的交汇问题，这些题的解题思路与解题方法基本一致，把这些题目作为一个专题进行复习，这就是所说的多题一解，这样可使学生学会归纳总结，少做题，提效率，起到事半功倍的效果，达到跳出题海的目的.