挖掘教材题根 引领思维生长
——以2021年新高考Ⅰ卷19题为例
广东 蒋海榕
(作者单位:广东省中山市实验中学)
教材是教师与学生最重要的学习资料.各类考试的题目通常来源于教材中的例题、习题的改编.我们把某一类型题目的来源称作题根.在新课标背景下,2019年人教A版新教材投入使用.挖掘新教材中的题根,以题根展开教学,来寻找解题思维入口;通过题根的变式拓展探求不同思路,帮助学生理解问题内涵和总结归纳,对提升学生思维有着重要意义.解三角形是高考中必考的一个知识点,它在考查基础知识的同时,还考查了数形结合、化归与转化、函数与方程等数学思想方法.本文以2019年出版的人教A版数学必修第二册的一道课后习题为题根,对解三角形的题根教学进行相关探讨.
一、挖掘题根,夯实思维基础

思路1:取BC边上的中点D,连接AD,如图,在△ABC中,∠ADB=π-∠ADC,
所以cos∠ADB=-cos∠ADC.
在△ABD和△ADC中,分别由余弦定理得,




思路3:如图,取AB,BC边上的中点E,D,连接DE,AD.









这是2019年人教A版必修二第53页的一道课后题.此题已知三角形三边,求三角形中线的长度.本文给出了五种解题思路:思路一是从几何图形中得到两个角互补的关系,得出余弦值互为相反数的结论,进而利用余弦定理化简求解;思路二是利用同一个角在不同的两个三角形中的余弦值相等求解;思路三是利用三角形中位线构造新的三角形,在新的三角形中利用余弦定理求解;思路四是在已有图形的基础上,将三角形补成平行四边形,再利用平行四边形的两对角线的平方和等于边长的平方和进行求解;思路五将解三角形与平面向量进行了结合,利用和向量模长来计算中线长进行求解.这道解三角形的课后题,考查的基础知识是余弦定理,却需要学生通过几何图形的特征,寻求解决问题的突破口.解题过程中渗透着数形结合、化归与转化、函数与方程思想;多种解题思路能够有效地提升学生的推理论证能力、空间想象能力、运算求解能力和创新能力,值得教师与学生挖掘其题根本质,进行迁移与拓展.
二、逐层变式,巩固思维广度

思路1:在△ABC中,

所以在△ACD中,





解:在△ABC中,由余弦定理可得
解得BC=4,


答案:4
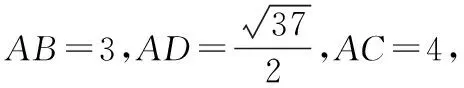



题根中是已知三角形三边求中线长,以题根为基础,我们可以进行以上变式.变式1和变式2是在题根的基础上改变条件:变式1是以三角形两边以及它们的夹角作为已知条件,变式2是以三角形两边及其中一边的对角作为已知条件,这两个变式都是求三角形未知边上的中线.文中只列出最简易直接的几种解题思路.变式3中,交换了变式1中的条件与所求.变式4中,仍以三角形中线为载体,改变条件和所求.变式5又是在变式4的基础上,将三角形中线改成一条边上的四等分点,逐层变式.虽是不同的变式,但是都可以在题根的模型基础之上,从几何图形中角的互补关系、同一角在不同三角形中的余弦值表示、平行四边形对角线与边长的关系、向量的模长等四个角度进行处理.5个变式,巩固了学生在解三角形解题过程中思维的多面性.
三、链接真题,提升思维高度
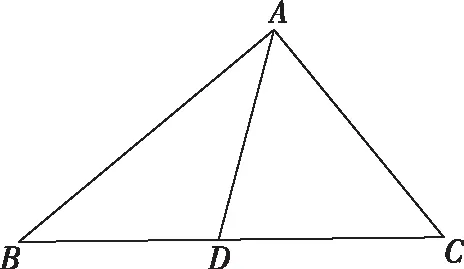
(2021·新高考Ⅰ卷·19)记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac,点D在边AC上,BD·sin∠ABC=asinC.
(1)证明:BD=b;
(2)若AD=2DC,求cos∠ABC.








这是2021年新高考Ⅰ卷中的第19题,我们主要探讨第二问.与文中题根对比,相似的是平面图形的几何特征,也可以理解为是相似的几何模型.所以题根中的四种解法都可以得到迁移应用.不同的是,题根与变式中,4个条件中AB,BD,BC,∠ABC都是已知3个,通过计算可以具体求出另外一个;而此题中4个条件中,仅知道BD=b,b2=ac,所以需要再列一个方程找到a,c的关系,通过联立才能具体求出cos∠ABC.此题源于题根,却高于题根;在题根的基础上,更强化了化归与转化思想.在解决这一系列问题的过程中,我们可以将以上内容进行拓展,得到两个一般性结论.






所以在△AED中,
《中国高考评价体系》明确指出,高考以“核心价值、学科素养、关键能力、必备知识”为考查内容,即“四翼”.解三角形作为高考重点考查内容之一,在正弦、余弦定理的基础上,利用图形的几何特征,找寻解决问题的思路,这类题型既能考查学生基本必备知识,又能考查学生直观想象、数学建模、逻辑推理与数学运算核心素养.解题过程中蕴含了数形结合、化归与转化等数学思想方法,所以我们在复习过程中,应当重视这部分内容对于提升学生思维的作用.教材中出现的例题与课后习题凝聚了众多专家的智慧,具有非常强的指导性.教师应该充分挖掘教材中的题根,从题根入手,通过变式与拓展不断增加思维的广度与深度,让学生在符合自身发展的探究中,理解问题内涵,体会一题多解、多题归一,以求达到真正促进学生思维再生长的效果.
——书写要点(三)

