圆锥曲线中易错问题致误剖析

陕西 刘正章

(作者单位：陕西省汉中市四○五学校)

解析几何的基本思想是运用代数法解决几何问题，由于其运算较烦琐，易出现失误，故解题时尽量运用几何问题中蕴含的几何性质简化运算，但由于几何图形灵活多变，稍有不慎就会出现漏洞.因此，在复习过程中要强化易错问题的教学与练习，下面简要谈谈圆锥曲线中的易错问题及其应对策略.

一、未能正确运用圆锥曲线的标准方程致误

“通过方程研究曲线的性质”是解析几何的两大基本问题之一，属于高考的必考点.因为我们研究圆锥曲线性质的经验主要是基于其标准方程，所以忽视圆锥曲线标准方程的掌握和正确运用，必将导致解题失误.

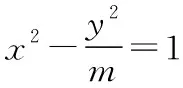
【错解】由双曲线方程得a=1，b=m，

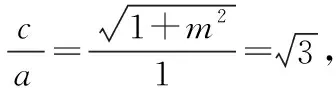
【剖析】本题主要考查的是双曲线的标准方程及其简单的几何性质，属于基础题.但标准方程中x2，y2的分母是a2或b2，错解中马虎大意，将y2的分母当成b，造成失误.

【正解】依据双曲线的标准方程，知a2=1，b2=m，

故应填2.

【评注】在圆锥曲线方程研究其几何性质时，要将方程化为标准形式，先“定位”，再“定量”.如焦点在x轴上的椭圆或双曲线，哪些量表示a2，b2，解题时必须弄清，另外还要注意a，b，c的关系，若是双曲线，则c2=a2+b2；若是椭圆，则a2=b2+c2，否则很容易出现错误.

二、未能正确运用圆锥曲线的定义致误

定义是辨析圆锥曲线的类型和推导其方程的根本，也是研究相应曲线上的点与其焦点距离有关问题的一把利器.但在运用定义时切莫忽视定义的前提条件，否则极可能出错.

A.直线B.抛物线

C.双曲线 D.椭圆

【错解】由条件知，点P到点(1，2)的距离与它到直线l：3x+4y-11=0的距离相等，根据抛物线定义知，点P的轨迹是抛物线，故选B.

【剖析】利用圆锥曲线的定义解题时，忽视了点(1，2)在直线l：3x+4y-11=0上的隐含信息，而只有当定点不在定直线上，两距离相等时轨迹才为抛物线.

【正解】由于点(1，2)在直线l：3x+4y-11=0上，且点P到点(1，2)的距离与它到直线l的距离相等，所以点P的轨迹是过点(1，2)且垂直于直线l的直线.故应选A.

【评注】利用圆锥曲线定义求轨迹是非常简洁的方法，但使用时需注意两个方面：一方面是定义的前提条件，如椭圆2a>2c，而双曲线不仅要满足2a<2c，还需关注是否有“2a>0”及“差的绝对值”；另一方面是数形结合时需考虑全面，否则易漏解致误.

三、未正确处理直线与圆锥曲线的位置关系致误

直线与圆锥曲线的位置有相离、相切、相交三种位置关系，在处理含参数的直线与圆锥曲线位置关系问题时，若忽视对参数，即直线与曲线位置关系的讨论，极易造成错解.

【例3】若过点(0，-2)的直线l交抛物线y2=8x于A，B两点，且AB中点的横坐标为2，则直线l与坐标原点的距离为________.

又因为y1=kx1-2，y2=kx2-2，x1+x2=4，

所以y1+y2=k(x1+x2)-4=4k-4，

于是k(4k-4)=8，解得k=-1或k=2，

所以l：y=-x-2，或y=2x-2.

【错解2】设l：y=kx-2，代入y2=8x，

得k2x2-4(k+2)x+4=0 ①，

又因为AB中点横坐标为2，所以x1+x2=4，

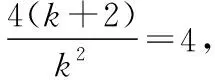
【剖析】错解1“点差法”默认了直线与曲线相交，反之则不然.事实上已知点不是弦的中点，按“点差法”也可求出弦所在直线的斜率，故运用“点差法”求中点弦须检验.错解2“根系法”默认方程①有两解，但该方程当k=0时，为一次方程；当k<-1，即Δ<0时，方程无实数根，这两种情况均不能使用韦达定理；当k=-1，即Δ=0时，虽能使用韦达定理，但此时直线与抛物线相切，与题意不符.故当k>-1，且k≠0，即Δ>0不可忽略.

【评注】解决直线与圆锥曲线的位置关系问题，常对交点运用“设而不求”的策略以减少运算量，但此法的前提是直线与曲线有公共点，因此求解过程中必须保证Δ≥0(相交于两点时Δ>0).另外注意两点：第一，判别式Δ=b2-4ac的使用前提是联立、消元后的方程ax2+bx+c=0满足a≠0，而当a=0时，对于抛物线属于直线与对称轴平行或重合的情形，对于双曲线属于直线与渐近线平行的情形；第二，直线与双曲线交于两点，可能都在左支、可能都在右支、亦可能是一左一右，若数形结合解题需分辨清楚.

四、忽视直线斜率不存在的情形致误

在求直线方程或研究直线与曲线位置关系问题时，往往要设直线方程，通常是直线过一已知点，设点斜式；没有明确的点、截距信息时，设斜截式.此时一定不要忘了斜率不存在的情形讨论，否则会出现逻辑不严谨或丢解错误.

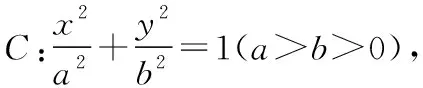
(1)求C的方程；

(2)设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为-1，证明：直线l过定点.

(2)设A(x1，y1)，B(x2，y2)及直线l的方程为y=kx+m(m≠1)，将直线与椭圆的方程联立，

得(4k2+1)x2+8kmx+4m2-4=0，

而-1=kP2A+kP2B

即(2k+1)x1x2+(m-1)(x1+x2)=0，将①代入，

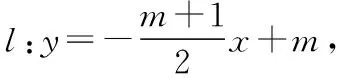
【剖析】第(2)问默认直线l的斜率存在，直接设其方程为y=kx+m(m≠1)，而忽视l⊥x轴时的情形，尽管经讨论与题设不符，但作为解答题必须要展示严谨的解决问题过程.

【评注】证明直线过定点的关键是设出直线方程，通过一定关系转化，找出两个参数之间的关系式，从而判断过定点的情况.在设直线方程之前，若题设中未告知，则一定要讨论直线斜率不存在和存在两种情况，接下来的通法是联立方程组，求判别式、韦达定理，结合题设关系进行化简.若已知直线不与y轴垂直，可设在x轴上的截距式x=ty+n来避免对斜率是否存在的讨论.特别提醒，此类问题归根结底属于待定系数法求方程的易错点，设方程时必须考虑所设方程的适用条件，不确定时切勿忽视对不适用情况的讨论.

(1)求椭圆C的方程；

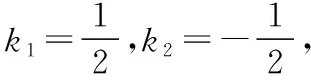
五、忽视圆锥曲线的取值范围致误

【例5】如图，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2=4x上存在不同的两点A，B满足PA，PB的中点均在C上.

(1)设AB中点为M，证明：PM垂直于y轴；

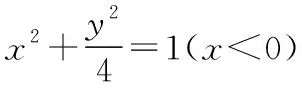
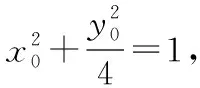
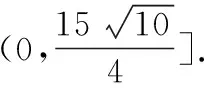
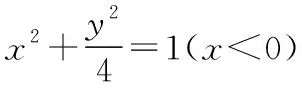
【评注】圆锥曲线中求范围问题，一般有两大类：

第一类是利用条件将目标问题转化为对应一元函数问题，再根据函数形式，选用方法求值域，如二次型利用对称轴与定义区间位置关系，分式型可以利用基本不等式，复杂或复合型可以利用导数，先研究单调性，再根据单调性确定值域.此时一定要注意自变量的取值范围，若自变量是已知曲线上点的坐标，则注意曲线的范围；若是关于动直线或曲线相交的参变问题，则注意判别式大于或等于0；若是已知参数，则注意相关约束条件.

第二类是建立目标问题的不等式，通过解不等式求解.该不等式来源于已知不等式关系(参数的范围、给定的不等式)、隐含的不等式(圆锥曲线的几何性质)、判别式等.

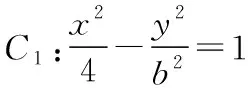
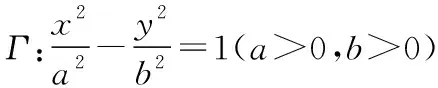
(1)若三角形ABF2可以是边长为4的正三角形，求此时Γ的标准方程；

(2)若存在直线l，使得AF2⊥BF2，求Γ离心率的取值范围.

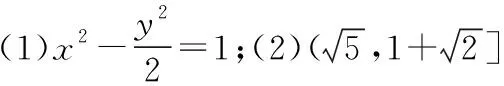
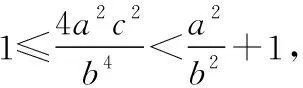
圆锥曲线内容较多，应用灵活多变，引起失误之处除上述常见五种情况外，还有如审题不严、概念混淆、计算出错、忽视隐含信息、忽视轨迹与方程的等价性、忽视参数的分类讨论、消参时忽视参数的制约条件等.限于篇幅，这里不再一一举例.

综上剖析，虽然有的失误影响较小，但大多失误却是“千里之堤，毁于蚁穴”，因此针对错误希望做到，有则改之无则加勉.只有在复习备考中有目的地强化圆锥曲线的定义、标准方程、几何性质、直线方程及直线与圆锥曲线的位置关系等知识的理解，掌握解决相关问题的思想、方法，形成良好的思维品质和解题习惯，才能尽量避免误入“雷区”！