巧用赋值法解决高考函数零点问题
山东 刘目勇
(作者单位:山东省淄博第六中学)
函数零点存在性问题在全国卷高考题中较为常见,如果在解决这些题目时选择参变分离就无法避免极限和数形结合的问题,这种做法在高考阅卷中肯定会出现扣分较多的情况.这是因为极限问题在高中阶段属于超纲内容,而数形结合在解答题中的运用又不太严谨,所以高考标准答案都是选择分类讨论、赋值然后运用零点存在性定理进行求解,这也是高中阶段最严谨的做法.但是答案中只会告诉我们把某个点代入是成立的,但是这个点是怎么找出来的,往往会让很多学生甚至老师都感到茫然,尤其是高考题中含参数的函数赋值就更是难上加难.常见的赋值方法有函数放缩赋值法、10 086移动取点法、分而治之取点法,其中函数放缩赋值法一般是标准答案采用的办法,本文主要通过剖析高考题对这三种方法进行初步探讨.
一、三种赋值方法的原理
1.函数放缩赋值法
比如要寻找x1使得f(x1)>0,若这样的x1不好寻找,我们就可以通过函数放缩解不等式f(x)>g(x)≥0,其中g(x)≥0是一个易解不等式,在g(x)≥0的解集中任取一个实数作为x1即可.常见的函数放缩不等式以及阶的比较如下:
(1)ex≥x+1,ex≥ex;
(2)当x>0时,ex>x2+1,ex>x2+x;


另外我们还需要知道无穷远处无穷大函数的阶的比较关系:c< 2.10 086移动取点法 3.分而治之取点法 【例1】已知函数f(x)=ae2x+(a-2)ex-x. (1)讨论f(x)的单调性; (2)若f(x)有两个零点,求a的取值范围. 1.当0 函数放缩法:f(x)=ae2x+(a-2)ex-x>(a-2)ex-x>a-2-x≥0得x≤a-2,故 2.当0 通过上面的分析我们可以看出,如果要运用函数进行放缩,应该大胆地进行添加、删除项或者根据函数不同的阶进行放缩,把不可解方程变为可解方程.如果采用10 086移动取点法应该在许可范围内取一个与10 086有关的点的值进行验算,当觉得问题复杂难解的时候分而治之也是一个不错的选择. 有了上面的分析我们可以选取一种放缩方法对此题第(2)问进行作答. 综上所述,f(x)有两个零点,a的取值范围为(0,1). 【例2】已知函数f(x)=(x-2)ex+a(x-1)2有两个零点,求a的取值范围. 解:f′(x)=ex+(x-2)ex+2a(x-1) =(x-1)(ex+2a). ①当a=0时,f(x)=(x-2)ex,此时f(x)只有一个零点,不符合题意, ②当a<0时,令f′(x)=(x-1)(ex+2a)=0得x=1或x=ln(-2a), 而f(1)=-e<0, f(ln(-2a)=[ln(-2a)-2](-2a)+a[ln(-2a)-1]2 =a{[ln(-2a)-2]2+1}<0, 所以x<1时f(x)<0,此时f(x)在(-∞,+∞)上最多有一个零点,不符合题意. ③当a>0时,f(x)在(-∞,1)上单调递减,(1,+∞)上单调递增.f(1)=-e<0,f(2)=a>0,所以f(x)在(1,2)内存在唯一的零点. 当x<1时,我们采用下面两种方法进行找点,我们可以令x<0. 方法一(函数放缩法): 方法二(分而治之取点法和10 086移动取点法相结合): f(x)=(x-2)ex+a(x-1)2>0, 所以f(x)在(x1,1)上存在唯一的零点. 综上所述,当a>0时,f(x)有两个零点. 下面给出两个练习,有兴趣的可以试一下. 【练习1】设函数f(x)=(1-x)2ex. (1)讨论f(x)的单调性; (2)当x≥0时,f(x)≤ax+1,求a的取值范围. 此题在第(2)问寻找矛盾区间时需要用到赋值技巧. 答案:(1)略;(2)[1,+∞) 【练习2】已知函数f(x)=(x-1)2ex,且f(x)在x=x0处取得最小值,函数g(x)=1+kx-lnx. 已知函数F(x)=min{f(x),g(x)},若在(0,+∞)上F(x)恰有三个零点,求实数k的取值范围. 答案:(0,e-2) 已知函数f(x)=(x+1)lnx-a(x-1).若当x∈(1,+∞)时,f(x)>0,求a的取值范围.(端点效应) 方法二:f(x)=(x+1)lnx-a(x-1)<(x+1)(x-1)-a(x-1)=(x-1)(x+1-a),取x1=a-1,则f(x1)<0,不符合题意. 综上,a的取值范围是(-∞,2]. 导数压轴题中常出现证明函数零点个数或已知零点个数求参数取值范围的问题.解答这类题的思路主要是结合函数的单调性,应用函数零点定理找出使函数出现正、负的函数值.其中找出符合零点定理成立的恰当数值是顺利攻克压轴题的难点.导数压轴题中的零点问题将继续是数学高考中的热点问题,“赋值”是关键,决定了数学尖子生水平的高低,教师和学生均需要多研究该类型的高考题和各省、市联考试题.函数寻找零点的赋值问题是高考中常见的问题,而寻找点的过程是学生学习的一个难点,本文只是对这类赋值问题的方法做了一个简单的介绍,希望有兴趣的读者继续研究并且提供更好的方法.

二、高考真题剖析










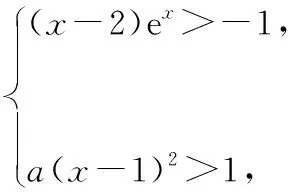
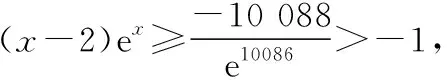


三、运用尝试及补充

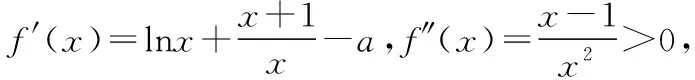

四、结束语

