一类数列压轴小题的探究

湖北 何 群 周天喜

(作者单位：华中科技大学附属中学 武汉市东湖中学)

在数列问题中有一类压轴题型，考查数列的单调性和有界性，实质上这类题型可以借助数形结合产生，属于它的特殊解决方法，即蛛网法，我们把这类题型称为蛛网模型.这类题型主要研究数列通项迭代关系，对于特殊的数列通项迭代关系，我们可以根据递推公式求出数列的通项公式，但对于一般的数列通项迭代关系，很难直接求出其通项公式，因此不能仅靠求出数列的通项来研究递推数列的有界性和单调性，而借助蛛网图这个工具可以很好地理解数列的变化趋势，从而更好地研究数列的单调性和有界性.

数列在历年的高考中有着重要地位，常与函数、方程、不等式等知识综合考查，因其综合性和探索性强，往往使得试题新颖且难度较大，不仅考查学生综合运用数学知识分析问题、解决问题的能力，也考查学生的思维品质和创新意识.

下面我们主要以湖北省部分重点中学2022届高三第一次联考数学试题第12题为例，展开针对高等数学中“蛛网法”的分析，以及通过数形结合解决迭代数列的变化问题的思考.

一、考题呈现

已知数列{an}满足：a1=0，ean+1+an=ean+1(n∈N*)，前n项和为Sn，则下列选项中正确的是(参考数据：ln2≈0.693，ln3≈1.099)( )

A.an+an+1≥ln2

B.S2020<666

D.{a2n-1}是单调递增数列，{a2n}是单调递减数列

解法分析：ean+1+an=ean+1(n∈N*)，

则an+1=ln(ean+1)-an，即有

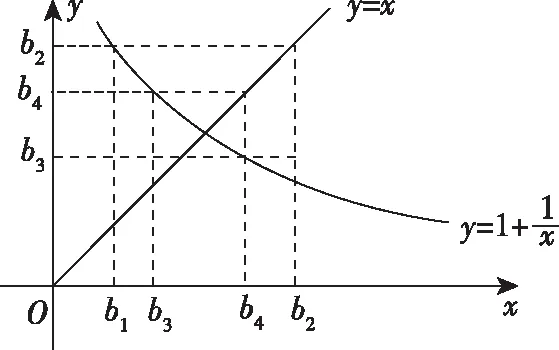
这种变化过程类似蜘蛛织网过程，所以简称蛛网图法.

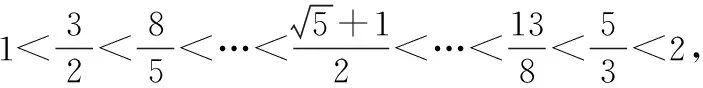
故选ACD.

分析：上述方法适用于an+1=f(an)(n∈N*)迭代生成的数列问题，往往不需要进行大量变形化简工作，借助数形结合即可很快发现其变化趋势，进而直接判断其单调性和有界性，很好地将烦琐的解题过程变得简单直观.

二、数列蛛网模型

数列蛛网模型主要研究数列通项迭代关系，主要题型是数列单调性和有界性.具体表现方式如下：

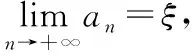
结合上述问题及理论分析可将其解题过程简单总结为三个步骤：一求，求构造的函数f(x)与y=x的交点，即可得到不动点，初步判定有界性；二画，画出y=f(x)与y=x的函数图象；三织网，织网过程就是呈现数列的变化过程.

(一)蛛网模型一(an+1=f(an)(n∈N*)

【例1】已知数列{an}满足a1=1，an+1=an+sinan(n∈N*)，则下列选项错误的是( )

A.an+1≥an

B.an≤2n-1

C.an≤π

D.an≤2

解：一求：根据an+1=an+sinan，构造函数f(x)=x+sinx，联立f(x)=x+sinx与y=x，求解得到sinx=0，则x=0，π，2π，…；

二画：在平面直角坐标系中画出f(x)=x+sinx与y=x的函数图象，再根据上一步求出的解即可明确两个函数图象的交点坐标；

三织网：根据a1=1的值，明确开始织网的位置，根据织网的规则进行操作.如图：

由图可知an

分析：此题通过蛛网图直接呈现出数列{an}的有界性和单调性，针对选项的思考明显简单很多，使得压轴变易.

A.(0，1)B.(1，2)

C.(2，3) D.(3，4)

分析：通过数列{an}的递推公式an+1=f(an)(n∈N*)构造的函数f(x)是一个二次函数类型，称为二次递推型数列问题，这样的数列问题往往是给定首项范围，以及递推公式，根据条件解决与数列有关的有界性或者单调性问题，或者在递推公式中插入参数，给出数列的单调性或有界性，进而求解参数取值范围.整体难度大，很难直接求出通项公式，所以借助蛛网图就可以将二次函数的图象与性质作为背景，根据二次函数与y=x的位置关系以及二次函数的开口方向、对称轴、顶点及特殊点等有关性质，直接判断对应数列性质，巧妙地化简了试题难度，使得蛛网助力，压轴变易.

(二)蛛网模型二(an=f(an+1)(n∈N*)

此模型与蛛网模型一有一定的区别，那么还能不能直接利用蛛网模型一的三步法求解数列问题呢？下面通过例题进行分析.

思考：很明显这里是an=f(an+1)(n∈N*)，与an+1=f(an)(n∈N*)有本质区别，模型一需要的是an+1用an来表示，但这里是an用an+1来表示.

解：一求：这里不再是构造关于an的函数形式，而是an+1的函数形式，类比模型一的特点，将其构造成关于y的函数f(y)=y2-y，即可得到方程y2-y=x；

二画：要画f(y)=y2-y的图象相对来说比较困难，但这里的f(y)=y2-y很明显与f(x)=x2-x是互为反函数，即关于y=x对称，我们直接画出f(y)困难，但是我们借助f(x)=x2-x的函数图象，将其关于y=x对称，即可得到相应的图象.同理，求解方程y2-y=x是将其看作关于y的一元二次方程，求得的解含根式，不便于画图象找交点，但其反函数f(x)=x2-x与y=x的交点横坐标很好解，即x=0或x=2，即f(y)=y2-y与y=x的交点横坐标也为x=0或x=2，如图：

三织网：根据数列{an}单调递增可知a1∈(0，2).

数列通项迭代关系的单调性与有界性考查很常见，但在高中阶段主要是以上呈现的两种数列蛛网模型，针对这类问题研究透彻很困难，本专题涉及的知识点多，过程繁杂，巧妙利用蛛网图，解决数列小题压轴题就可以了，所以在运用的过程中注意解题步骤(三步法)，即可把过程流程化、简单化，便于学生理解.