高考导向下概率统计题的命制创新与变式教学
——以两道概率与函数结合的原创试题及变式为例
湖北 周 威
(作者单位:恩施州教育科学研究院)
近年来,高考试题中概率统计解答题难度有所提高,其在试卷的编排位置并不固定,再加之试题情境新颖、阅读量增加、试题内容结构不定,因此概率统计试题备受评议,复习备考、试题预测难度加大,如何真正实施高效的复习策略和方法有待于一起探寻,而从模考试题的命制思路评析与分享未尝不是一种尝试和探索.
一、高考导向下的模考试题命制思路
(一)历年高考题的趋势导向
【情境1】(2021·新高考Ⅱ卷·21)一种微生物群体可以经过自身繁殖不断生存下来,设一个这种微生物为第0代,经过一次繁殖后为第1代,再经过一次繁殖后为第2代,……,该微生物每代繁殖的个数是相互独立的且有相同的分布列,设X表示1个微生物个体繁殖下一代的个数,P(X=i)=pi(i=0,1,2,3).
此情境设置为一种微生物群体的自身繁殖问题,第(1)问给出P0=0.4,P1=0.3,P2=0.2,P3=0.1,考查了该微生物个体繁殖下一代为一定概率时的分布列及期望,第(2)问将概率p与“x的方程p0+p1x+p2x2+p3x3=x的根”联系起来证明某结论及解释,都充分体现了高考“四翼”综合性、创新性,也是数据分析核心素养中“获得和解释结论”的主要表现.
【情境2】(2019·全国卷Ⅰ理·21)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
此情境设置为治疗某种疾病而研制的甲、乙两种新药治愈概率及治愈比较得分问题,第(1)问考查了甲药治愈得分的分布列,第(2)问将两种药治愈得分的概率与数列知识综合联系起来,以“证明{pi+1-pi}(i=0,1,2,…,7)为等比数列”与“求p4并解释”的形式给出题目设问.
以上情境第(1)问主要是考查分布列和数学期望,第(2)问都实现了知识点的跨越和融合,注意到一个是与“函数与方程”联系,一个是与“数列”联系,而数列本质也是函数,因此总的来说第(2)问都是实现了“概率”到“函数”的创新.因为概率可理解为“集合与数集”之间的映射,函数是“数集与数集”之间的映射,所以这种知识点的跨越也可以说连接了“映射”的数学本质.
从而概率统计模考试题命制方向可确定为第(1)问考查分布列与期望问题,第(2)问考查概率和函数(数列)融合的问题,主要体现概率统计思想与函数思想.
(二)基于情境“德育”导向的命题思路
2021年是全国党史学习教育的关键之年,为了更好地让中学生体会党史学习教育的重要性,彰显数学学科育人的德育价值,所以模考试题情境设置:某企业创新形式推进党史学习教育走深走实,举行党史知识竞赛,围绕竞赛设置期望和函数方面的问题.根据情境1与情境2,可分别设置如下命题思路:
【命题思路1】某企业创新形式推进党史学习教育走深走实,举行两轮制的党史知识竞赛初赛,每部门派出两个小组参赛,两轮都通过的小组才具备参与决赛的资格.该企业某部门派出甲、乙两个小组,进行党史知识竞赛.若第一轮比赛时,两组通过的概率分别是p1,p2,第二轮比赛时两组通过的概率分别是p3,p4.两轮比赛过程相互独立.
【命题思路2】某企业两部门创新形式推进党史学习教育走深走实,举行党史知识竞赛,比赛规则是:每轮比赛中每部门派出一个代表答题,两部门都全部答对或者都没有全部答对则均记0分;全部答对的部门记1分,没有全部答对的部门则记-1分.设每轮比赛中甲部门全部答对的概率为p5,乙部门全部答对的概率为p6,甲、乙两部门答题相互独立,且每轮比赛互不影响.
二、基于数据分析核心素养的命题意图
(一)分布列与期望的考查方式
数据分析是指针对研究对象获取数据,运用数学方法对数据进行整理、分析和推断,形成关于研究对象知识的素养.而题目中数据的设置与对分布列、期望的考查息息相关.首先,数据设置必须符合生活实际.那么对于命题思路1中,需要学生获取和处理的数据就是p1,p2,p3,p4,现在命题环节中如何确定这几个数值呢?第一轮比赛的难度通常要低于第二轮比赛的难度,故在每个小组通过的概率数值上是增大的,即p1>p3,p2>p4.这与情境1中已知的4个概率值递减类似.对于命题思路2中,需要学生获取和处理的数据就是p5,p6,因为要求两个部门总有一个要胜出,不妨设p5>p6.
其次,命题立意必须要清楚是要求“什么的期望”,期望的内涵是什么.因为获得、处理的数据要能解释结论,这正是数据分析核心素养的主要表现.
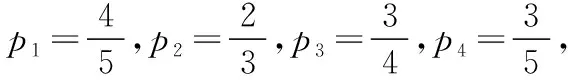
(二)概率与函数结合的考查方式
1.命题思路1中概率与函数结合的考查方式
如何实现概率到函数的跨越呢?依然可采用古典概型作为概率计算的背景:若参与决赛的小组由4人组成,每人必须且只答题一次,同时与答题顺序无关,每个成员答对每题的概率均相同,记为p,将其作为一个函数的自变量,这样就可以建立函数关系.参考情境1的设问方式,就得到了如下原创模考题1:
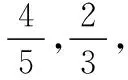
(1)若将该部门获得决赛资格的小组数记为X,求X的分布列与数学期望;
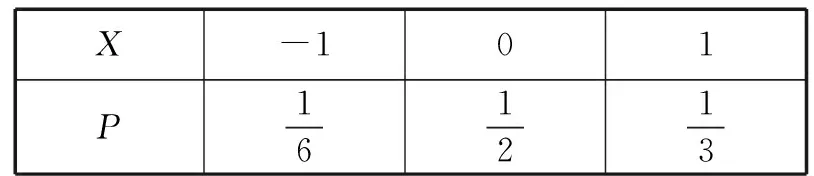
(2)比赛规定:参与决赛的小组由4人组成,每人必须答题且只答题一次(与答题顺序无关),若4人全部答对就给予奖金,若没有全部答对但至少2人答对就被评为“优秀小组”.该部门对通过初赛的某一小组进行党史知识培训,使得每个成员答对每题的概率均为p(0 解析:(1)设甲、乙两个小组通过两轮制的初赛分别为事件A1,A2.则 由题意X的取值可能为0,1,2.则 那么X的分布列为 X012P6251325625 则f(p)=6(1-p)2p2+4(1-p)p3=2p4-8p3+6p2. f′(p)=8p3-24p2+12p=4p(2p2-6p+3), 2.命题思路2中概率与数列结合的考查方式 (1)经过1轮比赛,设甲部门的记分为X,求X的分布列和数学期望; (2)若经过3轮比赛,用pn(1≤n≤3)表示第n轮比赛后的甲部门累计得分低于乙部门累计得分的概率,计算时发现满足函数关系式pn=a(b-qn),试求a,b,q的值. 解析:(1)由题意X的取值可能为-1,0,1. 所以X的分布列为 X-101P161213 经过三轮比赛,甲部门累计得分低于乙部门的三轮计分有四种情况(不计顺序):-1,-1,-1;-1,-1,0;-1,-1,+1;-1,0,0. 区域监测结果表明,例1与例2的难度系数均为0.2左右,属于较难题.那么这一结果出现的原因是什么呢?通过调查与分析发现,首先是一些同学不能读懂题目,对相互独立事件不理解;其次是例1第(1)问中学生不会进行数据分类,不能先将甲、乙两个小组分别通过初赛的概率计算出来,要么思维凌乱没有详细过程,要么出现计算错误;再次是例1与例2第(2)问中对二项分布理解不透,例1中不能正确的写出f(p)的表达式,有的表达式求对了,但不会运用函数相关知识求出p0;例2中不能正确写出p2,p3.这些出错原因与学生的数据分析核心素养水平以及函数思想有很大的关系.因此接下来的解题教学应是有目的、有层次、有导向的,针对学生数据分析核心素养的培养以及数学思维的提升进行变式教学. 根据例1、例2答题过程中学生的认知呈现水平及思维层次,可引导学生回忆相互独立事件、二项分布概念,分布列与数学期望的计算方法进行如下变式. 解析:若将该部门获得决赛资格的小组数记为X,则X的分布列为 X012P(1-p)(1-45p)p(1-45p)+45p(1-p)45p2 根据学生对概率的理解,在正确写出f(p)表达式的情况下,可引导学生开展拓展性思考.在命题立意不变、情境变化时,适当改变提问方式,那么关于概率的函数形式也会发生变化,能让学生体会问题解决过程中的数学本质. (1)设经过两次检测后两类剂型α1,α2合格的种类数为X,求X的分布列与数学期望; (2)若地区排查期间,一户4口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一使用试剂品α进行检测,如果有一人检测呈阳性,则该家庭为“感染高危户”,设该家庭每个成员检测呈阳性的概率均为p(0 解析:(1)与例1类似,略. 在概率统计的模拟试题命制及复习备考的解题教学中,若能尝试从学生“最近发展区”的特点出发,从试题的命题设计和其解题教学过程中进行分析和针对性变形与创新,打破试题的解题教学即“答案讲解”的僵局,不仅对学生数学核心素养的培养、关键能力的提升有重要的积极作用,也对跳出“题海战术”和减缓高三备考压力有很大的促进作用.
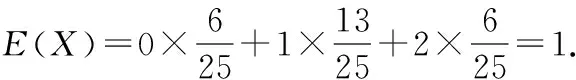


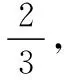
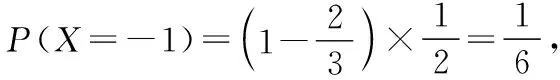
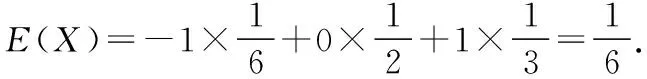
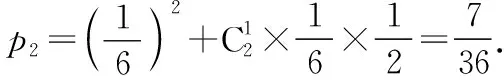
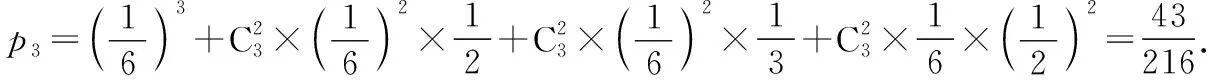
三、试题评价与变式教学
(一)情境不变,数学期望的设问改变
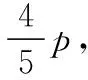
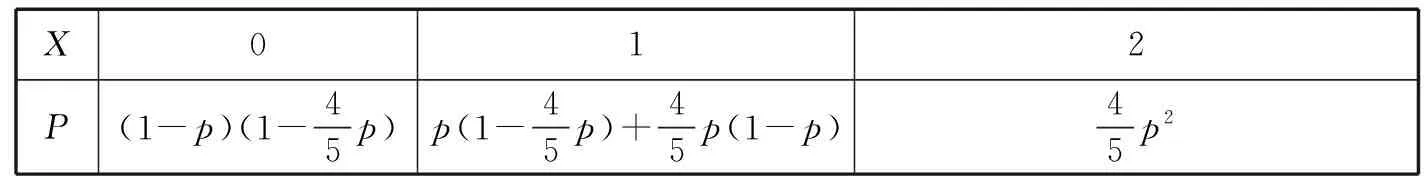

(二)因情境变化,关于概率的函数形式变化
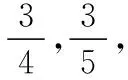

四、结语

