追根溯源探本质 变式拓展提能力——一道三角函数图象与性质真题的本质与变式研究

广东 雷雄军 朱广智

(作者单位：东莞市第六高级中学)

三角函数作为基本初等函数，是高中数学的一个重要内容，也是高考考查的热点模块.笔者研究2019—2021年高考全国卷发现，此模块知识主要以小题形式考查，通常一道客观题或者两道客观题，难度中等偏易.同时也发现三年中加强了对三角函数图象与性质的考查：如2021年全国乙卷理科选择题考查了三角函数图象的变换；2021年全国甲卷填空题考查了三角函数的性质；2020年高考全国卷Ⅰ理科考查了三角函数的图象与性质；2019年高考数学全国卷Ⅰ，卷Ⅱ理科选择题都考查了三角函数的图象与性质.笔者在教学过程中发现学生对三角函数图象变换中常见的“先平移后伸缩”和“先伸缩后平移”两种类型题目不能很好地作答.主要根源还是教师在平常的教学中没有注重知识本质的讲解，不会进行恰当的变式，化多为少，以一当十，让学生触类旁通，举一反三.现以2021年全国乙卷理科选择题第7题为母题，探究三角函数图象变换的本源，即通过四个恰当的变式，帮助学生巩固所学的知识，提升学生的解题能力和思维能力.

一、母题的选取及分析

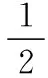
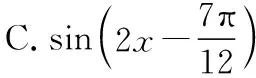
故选B.

课堂给学生做的过程中发现有部分考生出现了以下的错解：

二、母题本源深入探究

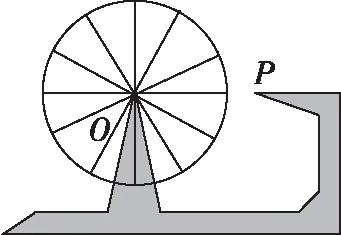
出现上面的错解的源头就是未能对函数y=Asin(ωx+φ)+b中参数ω，φ的意义理解透彻.旧教材中只对四个字母的几何意义进行了解释，A变换的几何意义是纵坐标的伸缩变换，ω变换的几何意义是横坐标的伸缩变换，φ变换的几何意义是图象的左右平移，b变换的几何意义是图象的上下平移.但是几何意义理解比较抽象，学生掌握起来比较困难.新教材在此章节上对函数y=Asin(ωx+φ)安排了专门的一小节内容，绕开了抽象的几何意义而是从具体的物理意义的角度解释A,ω，φ,b，x,y这六个变量，学生掌握起来比较容易.新教材以古代的一种水利灌溉工具筒车为具体背景，抽象出数学模型如图所示：

得到盛水筒P距离水面的高度H与时间t的关系式：H=rsin(ωt+φ)+h，r的物理意义是振幅即筒车的半径，ω的物理意义是筒车旋转的角速度，t的物理意义是运动的时间，φ的物理意义是盛水筒的初始位置，h的物理意义是筒车中心到水面的距离.由正弦函数图象y=sinx变换到函数y=Asin(ωx+φ)+b图象过程中，学生理解的难点在参数的ω，φ变换上.下面从物理意义直观理解先变φ后变ω与先变ω后变φ的区别(假定ω>0,φ>0).

先变φ后变ω：

=sin(ωx+φ)

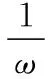
先变ω后变φ：

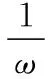
三、母题的变式拓展探究

有了上述对参数的具体物理意义的理解，学生对这个题目可以轻松解答.我们都知道高考真题是经典的数学试题，为了发挥其应有的价值，在教学过程中我们就要注重对其进行变式拓展延伸，这样不仅能够帮助学生深入理解要学的知识，还有助于培养学生灵活的思维方式，培养学生的求异思维，创新能力，提升学生的应变能力，让课堂教学成为真正的高效课堂.笔者从以下四个方面对此题进行了变式.

变式一：如图，一个摩天轮的半径为10米，轮子的最底部距离地面2米，如果此摩天轮按照逆时针转动，每4分钟转一圈，且当摩天轮上某人经过点P处(点P与摩天轮中心高度相同)时开始计时，则经过1分钟后此人相对地面的高度为______米；在摩天轮转动一圈内，此人相对于地面高度不低于17米的时间为________秒.

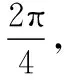
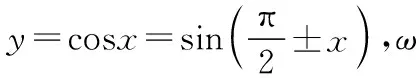
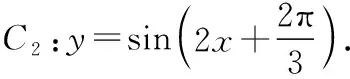
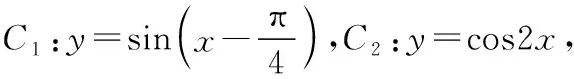
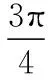
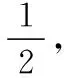
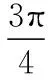
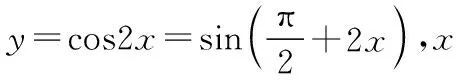
四、结语

变式教学在数学课堂教学中具有非常重要的意义，上面由一个看似简单的三角函数图象变换的高考真题出发，通过对其参数具体物理意义的本源探究，及其对题目多角度层层递进的变式探究，有效地深化了对三角函数图形变换知识的理解与掌握，突破了三角函数图形变换中的难点，开拓了学生的解题思维，有效促进了学生思维品质的改善和创新能力的提升.尽管高考试题不断地推陈出新，但其原型还是来源于我们的教材，来源于我们平时做的习题，所以我们教师在平时的教学过程中，要注重对学生所学的知识点，所做的题目进行有目的的变式训练.新授课时，变式教学要注重对情境问题进行变式探究，如本课试题可以将筒车变式为学生熟悉的摩天轮，然后设置相关问题，通过情境问题变式，增加学生对问题的思考，进而更好地理解即将要学的新知识.习题课时，对题目的变式要注重立足于原有的题目(不能脱离原有的题目)，通过对题目中的条件、结论多角度、多视角切入变式探究，真正做到“一题多思”“一题多问”“一题多变”.巧妙地把题目中丰富的知识底蕴充分挖掘出来，形成一个有效的知识网络体系，真正提升学生解题能力，拓展数学应用.