注重方法比较 善于变式拓展——以一道向量模拟题的深度探究为例

贵州 李 寒

(作者单位：贵州省贵阳市第一中学)

向量是近代数学中重要和基本的概念之一，有着丰富的几何背景，是解决几何问题的有力工具.它具有几何形式和代数形式的“双重身份”，能将数形融于一体，能与中学数学教学内容的许多主干知识综合，形成知识交汇点，成为“在知识网络交汇处设计试题”的良好载体.下面对一道向量线性运算与基本不等式交汇问题的解法进行探究，以体会方法优化的重要性，通过对问题的变式扩展，以揭示这类问题的本质和规律.

一、试题呈现

该题是平面向量与基本不等式应用相结合的一道填空压轴题，将直线过重心G转化为向量表示，再结合已知的向量关系，推导出关于m，n的式子，最后利用基本不等式求解得到答案.

二、解题探究

1.解法赏析

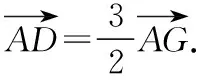
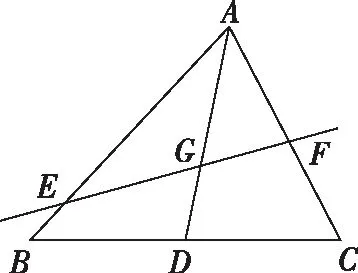
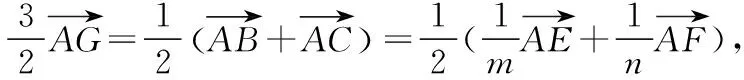
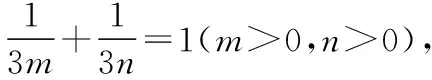
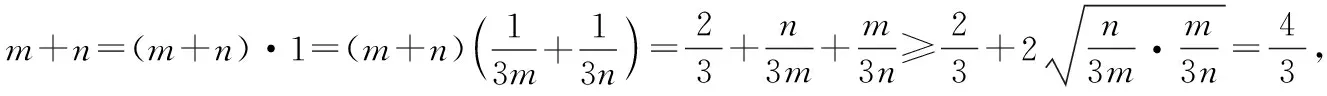
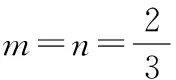
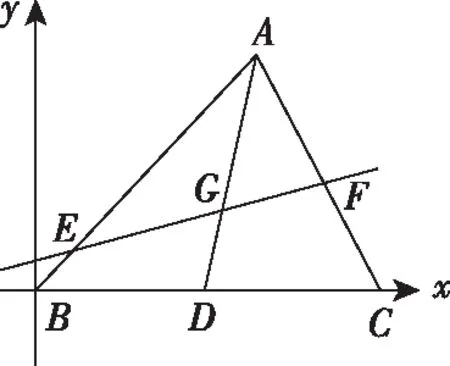
解法2(向量坐标法)：连接AG并作AG的延长线交BC于点D.

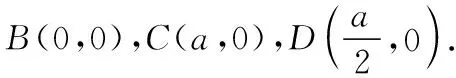
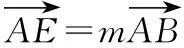
所以x1=(1-m)p，y1=(1-m)q，所以E((1-m)p，(1-m)q).

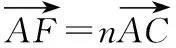
所以x2=na+(1-n)p，y2=(1-n)q，所以F(na+(1-n)p，(1-n)q).

点评：解法2通过建立直角坐标系，将问题用向量坐标表示，通过向量的坐标运算，使问题程序化，其目标明确，思路清晰，思维难度小，但向量坐标法的运算量较大，对数学运算核心素养要求较高.

解法3(几何法)：如图，连接AG并作AG的延长线交BC于点D.

因为点G是△ABC的重心，所以点D是BC的中点，即BD=DC.

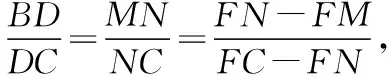
点评：解法3利用了平行线分线段成比例定理，得到线段的比例关系后，将已知条件的向量关系转化为线段长的比例关系求解.几何法别出心裁，过程简洁、条理清晰，对逻辑推理核心素养要求较高.

2.方法比较

向量所具有的“数”与“形”的双重特征，为数形结合提供了良好的载体.求解向量有关问题通常有两种思路：一是“形化”，即从向量基底法的角度思考，基底法是解决向量问题的通性通法；二是“数化”，即从坐标法的角度思考，坐标法是解决向量问题的常用方法.根据上述给出的三种方法，比较得到如下结论：

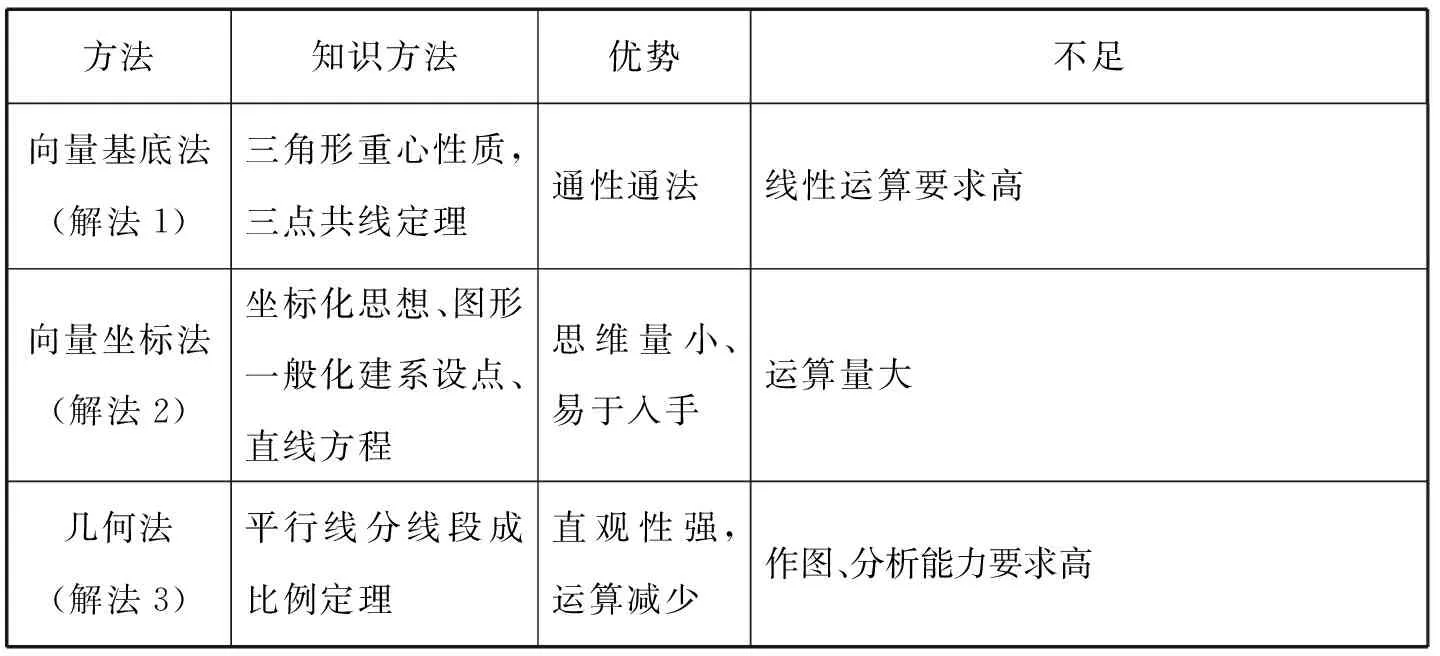
方法知识方法优势不足向量基底法(解法1)三角形重心性质,三点共线定理通性通法线性运算要求高向量坐标法(解法2)坐标化思想、图形一般化建系设点、直线方程思维量小、易于入手运算量大几何法(解法3)平行线分线段成比例定理直观性强,运算减少作图、分析能力要求高

上述思路方法体现的均是中学数学解题的思想和方法.虽然在高考复习备考的临考阶段时间紧、任务重，但对典型试题的解答要主动归纳总结各种不同的方法，并熟练掌握处理问题的通性通法，在掌握基本方法的同时，要学会分析、比较、优化解题方法，唯有如此，当学生遇到不同问题时，才会选择恰当的方法，解题时少走弯路.

3.延伸结论

上面解题过程中，其实蕴含着直线过三角形重心的一个充要条件的结论，即

三、变式探究

探究1：若上述问题中直线EF不过重心G，会有怎样的关系呢？探究如下：

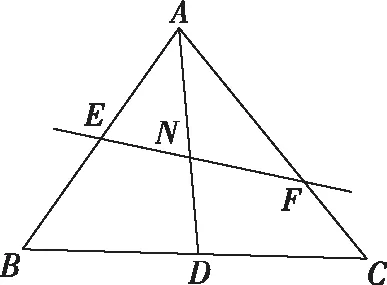
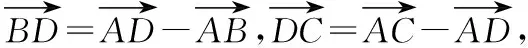
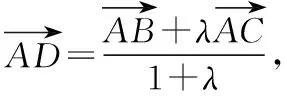
其实，若将变式1中向量关系做一下变动，可得到：

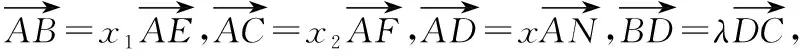
若进一步将向量关系变为线段比值关系，可得到：

根据推论1，也可以得到：

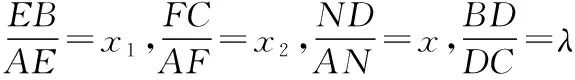
推论1、2将三角形中的某些线段的长度之比统一到一个公式中，其结构、形式与解析几何中的定比分点坐标公式一致，简洁、整齐、易记，故称为几何“分点坐标公式”，利用该定理可以解决平面几何中，三角形被直线所截得的线段比的一类问题.

探究2：若将变式1研究的方向改为求向量的数量积，又会是怎样的情形呢？探究如下：

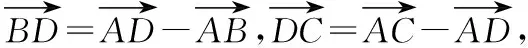
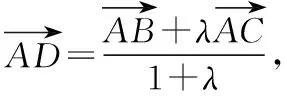
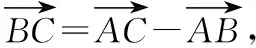
由此，我们可以得到一般性结论：

特别地，若D为△ABC的BC边的中点，即λ=1，则有：

相比较而言，命题2的推论具有更广泛的应用.

四、应用举例

解析：如图，连接BE交AC于点H，设正六边形ABCDEF的边长为1，则由正六边形的性质可得BE=2.

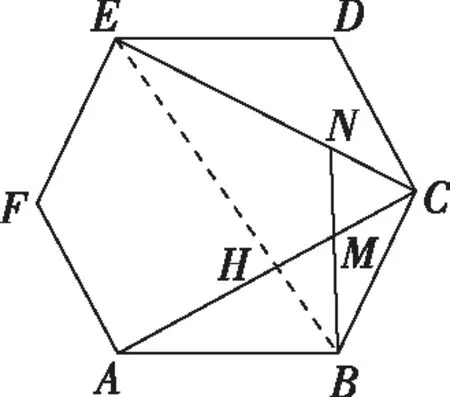
在Rt△CHB中，因为∠BCA=30°，

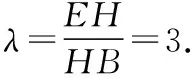
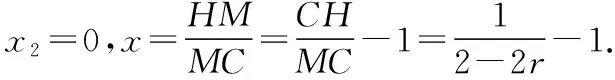
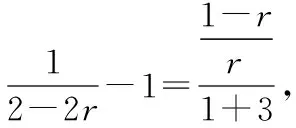
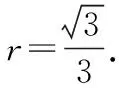
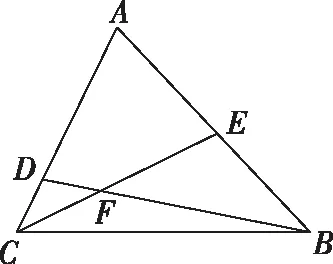
解析：设△BCF的面积为S，

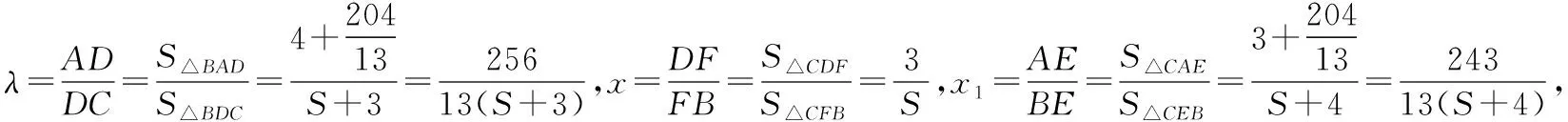
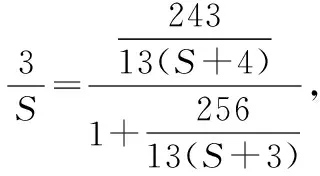
整理得17S2-26S-295=0，

所以(S-5)(17S+59)=0，

故△BCF的面积为5.

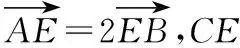
A.-6B.-3

C.3 D.6

五、教学启示

在高考复习备考的临考冲刺阶段，想要打造精准、高效的教学课堂，需要从根本上改变教与学的方式，发展学生解决问题的意识和能力.数学解题是巩固基础知识、落实基本技能、感悟思想方法、提升思维敏锐度的系统活动，数学教学研究的过程主要就是解决问题的过程，掌握数学知识的一个重要标志就是善于解题.特别是在讲评课中，对典型问题的一题多解、同型归类是不错的选择.与此同时，要从已经解决的问题入手，对问题延伸、挖掘，进行变式探究，寻找到处理此类问题有效的规律和方法，培养学生的探究意识和解题能力.总之，对典型试题适宜地进行对解法、变式及拓展等方面的教学与训练，既能梳理解决这类问题的一般方法，寻求解答此类问题的通性通法，揭示问题的本质和一般规律，又能拓宽学生的知识面，权衡解法优劣，积累解题经验，让学生走出“题海”，提高复习时的解题效率，力争在2022年高考中取得优异的成绩.