“垂直平分线”和“角平分线”的应用
阮秋月


【摘要】“垂直平分线”和“角平分线”是学习初中数学和解决数学问题中常遇和常用的“两线”,它们在定义、性质和判定等方面具有一些相通点.本文尝试在分析这些相同点的基础上,寻找用“两线”解决问题的巧妙之处,从而帮助初中生更高效的解题.
【关键词】“垂直平分线”;“角平分线”;数学解题
“垂直平分线”和“角平分线”作为初中数学几何部分的内容,在代数部分也举足轻重,尤其是在压轴题中其综合性体现得非常明显.同时,“两线”结合也是学生解题的难点所在,如何巧妙应用“两线”解决数学问题,对提升学生的解题效率和准确率非常关键.
1 “垂直平分线”和“角平分线”的相通之处
“垂直平分线”和“角平分线”虽然是初中几何部分两个不同的教学内容,但是它们的知识点安排,如定义、性质、判定、尺规作图等,具有异曲同工之妙.教师要想学生能够灵活、巧妙的利用“垂直平分线”和“角平分线”解决数学问题,就要让学生对这“两线”各自的内容及其相通之处有所了解[1].本文认为,“垂直平分线”和“角平分线”的相通之处主要体现在以下四个方面:
首先,定义相通.从“垂直平分线”和“角平分线”这“两线”的定义不难看出,“垂直平分线”重在说明线段被平分,而“角平分线”重在说明角被平分.所以,从“垂直平分线”和“角平分线”这“两线”在定义方面的相通之处在于“平分”,即抓住了“平分”也就抓住了从“垂直平分线”和“角平分线”这“两线”的定义.
其次,性质相通.从“垂直平分线”和“角平分线”这“两线”的性质可以看到,“垂直平分线”和“角平分线”这“两线”都重在说明“距离相等”,这是它们的相通之处.不同的是,“垂直平分线”中的“距离”是指点到点的距离,而“角平分线”中的“距离”是指点到边的距离.总之,抓住“距离相等”和“点到点的距离”、“点到边的距离”几个关键词,就可以掌握“垂直平分线”和“角平分线”的重点和难点.
再次,判定相通.“垂直平分线”和“角平分线”的判定都是证明一条线的属性或归属.如“垂直平分线”的判定定理证明的是一条直线是一条线段的垂直平分线,“角平分线”的判定定理证明的是一条射线是一个角的平分线.但需要注意它们的不同,那就是证明一条直线为垂直平分线时,需要分别证明两个不同的点在这条直线上,而证明一条射线为角平分线时,需要说明这个点在这个角的内部[2].由此可见,抓住了它们的不同之处,也就抓住了它们的本质.
最后,作法相通.从“垂直平分线”和“角平分线”的尺规作图方法不难看出,“垂直平分线”的尺规作图方法是“角平分线”的尺规作图方法的基础,都要以两个不同的端点为圆心,都要以大于线段二分之一的长度为半径,都是两条圆弧的交点.换言之,“角平分线”的尺规作图是在“垂直平分线”的尺规作图基础上进行的[3].另外,作法相通还表现在图形的构造上,都凸显了全等三角形和等腰三角形.第一,在作“垂直平分线”时,圆弧的交点和线段端点、垂直平分线就构造出了两个全等的三角形,在这作“角平分线”时,两种不同圆弧的交点与角平分线就构成了两个全等三角形.第二,线段两个端点和一个圆弧交点形成的图形为等腰三角形;画角平分线的理论依据就是等腰三角形的“三线合一”,即底边的垂直平分线和顶角的角平分线“合二为一”,这里再一次说明了“垂直平分线”的尺规作图方法是“角平分线”的尺规作图方法的基础.
2 基于“两线”的初中数学题巧解思路
2.1 利用“平分”巧解
例1
如图1所示,在△ABC中,∠ACB=90°,BE平分∠ABC,交AC于点E,DE垂直平分AB于点D.
求证:BE+DE=AC.
点拨与解析本题是典型的“垂直平分线”和“角平分线”结合问题.由于BE、DE和AC很难发现他们之间的数量关系,但是可以通过转化的方法将这三条线段化为一条,这就是数学中典型的化归思想.具体可以按如下步骤操作:首先需要借助“垂直平分线”的性质将BE和AE相互转换,然后要利用“角平分线”的性质将CE和DE相互转换.在转换之后,便容易由AC=AE+EC得到AC=BE+DE.
2.2 利用“距离相等”巧解
例2
如图2所示,已知∠AOB 平分线上一点E,且EC⊥OA,ED⊥OB,垂足分别为点 C,D.
求证:(1)OC=OD;(2)OE是CD的垂直平分线.
点拨与解析 本题中两次利用到了“距离相等”,第一次是利用了角平分线中的“点到边距离相等”,即DE=EC,第二次是利用了垂直平分线的“点到点距离相等”,即OD=OC,这是“垂直平分线”和“角平分线”中典型的“距离相等”相通之处.看到“∠AOB 平分线上一点E,且EC⊥OA,ED⊥OB”,马上就要想到是角平分线的性质,看到“OC=OD”,马上就要想到是否与线段的垂直平分线有关,这都是灵活解题的表现.而“垂直平分线”和“角平分线”还有“全等三角形”相通之处,所以(1)(2)两问是否可以借助这一相通之处解决就变得非常重要.
2.3 利用“全等”巧解
例3
如图3所示,在△ABC中,DF是边BC的垂直平分线,AD是△BAC一个外角的角平分线,DF与AD相交于点D,DE⊥于 E,且 AB > AC.
求证:BE-AC=AE.
点拨与解析 本题是要证明BE、AC、AE三边之间的关系,而从图形中不难发现AB-BE=AE.很明显,这需要构造三角形并证明它们全等,恰巧“垂直平分线”和“角平分线”有一个相通之处是“作法相通”,根據上文分析其实就是“三角形全等”.基于此,就应该马上想到如何利用“垂直平分线”和“角平分线”构造出“全等三角形”,而这就需要连接DB和DC,同时还需要过D点作DM⊥AC.这样作辅助线的灵感主要来自三个方面:其一,连接DB和DC是由“DF是边BC的垂直平分线”这个条件想到;其二,过D点作DM⊥AC是由“AD是△BAC一个外角的角平分线”这个条件想到;其三,构造“全等三角形”是由“BE-AC=AE”这个条件想到.
2.4 利用“相等”巧作辅助线
例4
已知,如图4所示,点B、C在∠A的两边上,且AB=AC,P为∠A内一点,PB=PC,PE⊥AC,PF⊥AB,垂足分别为E、F.
求证:PE=PF.
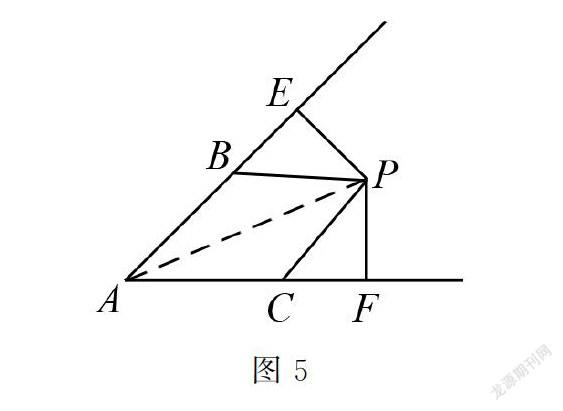
点拨与解析 本题是非常典型的“两线”问题.在“两线”问题中,往往需要依靠作辅助线才能得到解决,而如何作辅助线,其中有一定技巧,抓准题中“相等”关系的量非常关键,如本题中的“AB=AC”、“PB=PC”,都是巧作辅助线的突破口.所以,本题的解决思路大体是:首先,如图5所示连接AP.然后,根据
AB=AC、PB=PC,外加一条公共边AP,就证明了△ABP和△ACP是全等三角形,在此基础上得到∠BAP=∠CAP.再结合P为∠A内一点,得到AP为∠A的角平分线.最后,根据PE⊥AC,PF⊥AB,结合角平分线的性质可知PE=PF.需注意的是,首先,本题中证明AP是∠A的角平分线不能仅凭∠BAP=∠CAP这一个条件得到,而需结合P为∠A内一点这個条件,因为“角平分线的判定”中明确了“在角的内部”这一基础条件,切勿遗漏.其次,本题中综合了角平分线的性质和判定,而这学生对这两大内容极易混淆,在本题解决过程中切勿因混淆而致错.
3 “两线”问题解决过程中应避免的错误
在初中数学几何部分,“垂直平分线”和“角平分线”是非常重要且基础的两个知识点,其一方面体现在知识体系规善上,另一方面体现在解题思维拓展上.但是,无论从哪个方面审视该知识点,都应注意以下易错点的规避:
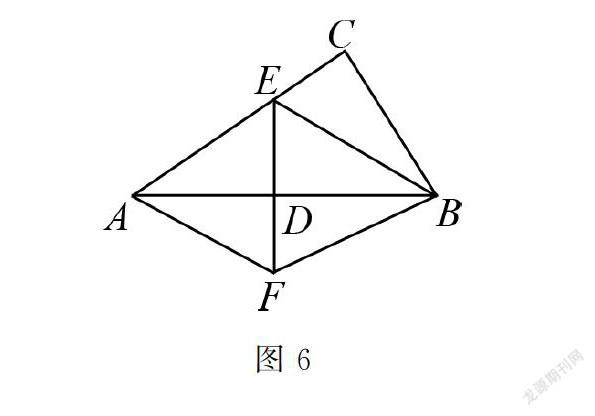
第一 准确理解“平分”.相对而言,角平分线中的“平分”比较容易理解,无论是在其性质还是判定都是如此.这里所说的准确理解“平分”,重点在于垂直平分线.如图6所示,由于DE垂直平分AB,易得DE⊥AB和AD=DB,这是正确的解题思路.但是,很多同学容易在类似于图6的问题中出错,认为在DE垂直平分AB的情况下还可以得到ED=FD.
第二 准确区分性质与判定.无论是垂直平分线,还是角平分线,它们都有性质与判定.
首先,垂直平分线的性质是“线段垂直平分线上的点与这条线段两个端点的距离相等”,垂直平分线的判定是“到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.即线段垂直平分线可以看成到线段两端点距离相等的点的集合”.不难看到,垂直平分线的性质和定理是互逆的,要想精准掌握,还需仔细揣摩.这里需注意的是,在判定垂直平分线时,需证明两个点同时在一条直线上才能得到该直线为垂直平分线上,这是学生极易犯错之处.如图6所示,只依靠AE=BE,DE垂直AB只能证明点E在直线EF上,还应用同样的方法证明点F也在直线EF上,然后才能得到直线EF是线段AB的垂直平分线.另外需注意的是垂直平分线是直线,而角平分线是射线,这是它们的本质属性.
其次,角平分线的性质是“角平分线上的点到角两边的距离相等”,角平分线的判定是“角的内部到角的两边距离相等的点,都在这个角的平分线上”.这里需要注意的是,“角平分线的判定”中明确了“角的内部”这一基础条件,证明时切勿遗漏该条件.正如例4中,在证明AP是∠A的角平分线时,一定要结合“∠BAP=∠CAP”和“P为∠A内一点”两个条件.要知道,在例4中明确给出了“P为∠A内一点”,学生在解本题时要意识到这一条件绝对不是命题者“多此一举”.
参考文献:
[1] 刘顿.两线联姻,轻松解题[J].初中生之友,2011(29):32-33.
[2] 王友峰.“三用”线段垂直平分线和角平分线定理解题[J].初中生学习指导:初三版, 2012(17):103-105.
[3] 赵兴荣,祁乐珍.线段垂直平分线与角平分线的“证”与“用”[J].数学学习与研究, 2011(20):86-86.

