学生数学解题心理性错误例析

励剑杰

摘 要： 学生在解题过程中总会出现各式各样的错误，受心理因素的影响，虽然掌握了解题的知识点和技巧，但还是常出现心理性错误.本文阐述了心理性错误的原因，分析解决的策略，使学生尽量避免心理性错误.

关键词： 数学解题 心理性错误 视觉性错误 干扰性错误

在学习过程中，学生往往会出现各种错误，错误是通向成功的阶梯，如果教师能进一步分析学生犯错误的原因，在错误上做足文章，就可以找到学生出错的根源，并做相应的处理，相信学生可以有所改观.

解题错误主要分为知识性错误、逻辑性错误、策略性错误和心理性错误等.教师更多地关注于知识性错误、逻辑性错误和策略性错误，较少关注学生解题的心理性错误.心理性错误主要指解题主体虽然具备了解决问题的必要知识与技能，但由于某些心理原因而产生的解题错误.如顺序心理、滞留心理、潜在假设，以及看错题、抄错题、书写丢三落四等.

案例：陈学生平时在校表现较好，学习态度端正，认真刻苦，但作业质量不大高，考试分数不高.起初我以为是家里学习不用功，当面一套背后一套，但与家长联系后得知在家学习也很用功.带着这份好奇，我开始关注陈同学在数学解题上的错误.我问她错误原因时，她最多的回答就是“看错了、写错了”.我总是提醒她下次审题仔细点、解题仔细点.以下是我与陈学生的某次对话片段：

师：陈某某，你怎么老是解题这么粗心，又犯低级错误.

生：我也不知道，老是算错……

师：考试的时候你是不是很想考好？

生：是的.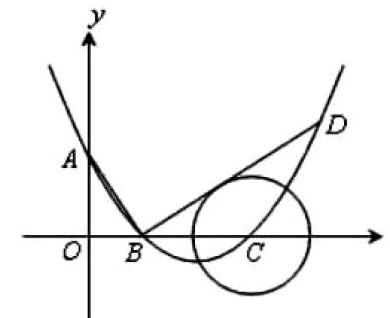

师：考试的时候常怀疑自己会犯低级错误吗？很想考好，使劲想不算错、不看错……

生：嗯.

师：你相信自己能做得更好吗？

生：……（沉默）

我想通过心与心的沟通找到解决问题的方法，但开始一段时间的不断交流没有换来我期待的结果.我一边关注陈学生，一边结合大部分出现心理性错误的学生实际情况，分析形成心理性错误的原因.

大多数学生总是能立即认识到自己在解题过程中“粗心”，但其中很大一部分学生还是会程度丝毫不减地犯“老毛病”.这其中的“粗心”一次次地折磨着学生，尤其应当引起教师的注意.让我们从学生的心理因素来分析，“粗心”造成的解题出错往往是心理性错误，大致可分为两类：视觉性错误和干扰性错误.

1.视觉性错误

视觉的感受器是眼，眼与视神经、大脑皮层的有机联系就形成了视觉.数学问题的这一知觉对象的各个部分对大脑的刺激具有强弱的差别，强知觉对象往往会抑制弱知觉对象在大脑中产生的兴奋，造成对弱知觉对象的暂时遗忘而出错.比如学生在回答如下问题“已知圆的直径为9cm，如果圆心到一条直线的距离为5cm，那么这条直线和圆的位置关系是？摇？摇 ？摇？摇.”时，常常会更多地关注直线与圆的位置关系，而忽略条件中9cm是直径还是半径.

2.干扰性错误

干扰发生的心理原因，是当人的感觉器官受到某一强刺激的持续作用时，神经中枢就产生相当稳定的、集中的兴奋，形成优势兴奋中心，由于优势原则的影响，在解题时，常常形成干扰而造成错误.具体表现如下.

（1）定势性干扰

如：“若圆锥的底面半径是3，母线是4，则这个圆锥的高等于？摇 ？摇？摇？摇.”通过构造直角三角形，三边长为3、4、5，因此，此题的答案是5.定势性干扰使学生根本没有区分直角边和斜边.

（2）经验性干扰

（3）思维性干扰

如：“在平面直角坐标系中，顶点为（4，-1）的抛物线交y轴于A点，交x轴于B，C两点（点B在点C的左侧）.已知A点坐标为（0，3），已知点P是抛物线上的一个动点，且位于A，C两点之间，文：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的左边和△PAC的最大面积.”连接AC，由于AC的长度不变，因此，点P到直线AC的距离越大，△PAC的面积越大.由于存在这样的思维性干扰，接下来的解题可想而知.当与AC平行的直线与抛物线只有一个交点时，这个交点即为点P，此时的△PAC的面积最大……按此思路解题，不但过程繁复，计算量大，而且很多学生受思维性干扰很难得出正确答案.

以上是对解题过程中常见的两类心理性错误的原因进行了分析，实际上，学生出现的心理性错误，往往是由一个或几个原因交织而成的，这是一个值得深入探讨的问题.针对上述心理性错误的表现及成因，教学中要着重使学生克服紧张情绪，以平和的心态解题，具体做法如下，供参考.

1.提高学生的自我效能感

学生的自我效能感直接影响学生的解题心理.自我效能感高的学生解题能从容应对，而自我效能低的学生解题时会出现不自信、紧张等不良的心理问题.尤其在考试时，在有限的时间里全面考查学生的知识掌握程度，自我效能感低的学生更容易出现心理性错误.在个案中的陈学生就是不够自信，因此，我时常鼓励她相信自己可以做得更好，给她在全班同学面前表现的机会，发现她有丝毫进步都及时给予表扬.经过我长期的鼓励和表扬，陈同学在数学解题上明显变得自信多了，能冷静分析，认真审题，视觉性错误基本没有.

2.展现错误，拓展学生思维

学生的错误解题有些是具有共性的，把共性的错误展现在全体学生面前有助于学生直面错误，通过学生之间的讨论解决解题中的错误.在教与学的过程中，充分暴露思维过程，特别是暴露思维受阻，在解决某一道题目时出现思维受阻，如何继续解决，这样的思维训练必将有助于学生弄清解题过程的有效层次，形成正确的心理势态，克服思维性干扰，以探求到正确的解题途径.这样的教学过程必然有助于学生养成思维严谨、勇于面对挫折等良好的数学品质.

3.加强变式教学和训练

在教学中，提供充分、全面的变式，能帮助学生从事物的各种表现形式和事物所在的不同情境中认识事物的本质属性，对概念、解题方法等的理解更精确，更概括，更易于迁移.

如，如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D，求证：AC平分∠DAB.

变式1：若AB为⊙O的直径，C为⊙O上一点，过C点的切线交AD于点D，AC平分∠DAB，则AD⊥CD.

变式2：若AB为⊙O的直径，C为⊙O上一点且AD⊥CD于点D，AC平分∠DAB，则CD是⊙O切线.

变式3：若点A、B、C在⊙O上，AD和过C点的切线互相垂直，垂足为D，AC平分∠DAB，则AB为⊙O的直径.

变式4：若AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D，AD交⊙O于点E，连接OC、BE交于点F，则（1）四边形CDEF是矩形；（2）BE=2CD.

变式6：若AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D，AD与BC的延长线交于点M，则（1）AB=AM，∠M=∠B，CM-CB；（2）△CDM∽△ADC∽△ACB.

变式教学和训练可以优化学生的认知结构，提高学生的审题和解题能力.“粗心”的学生通过变式训练，从一系列的题目中会自主发现之间的区别与联系，审题、解题不仔细的弊病可以逐渐得以消除.

参考文献：

[1]罗增儒.数学解题的错例分析.中学数学教学参考，2009. 7：15-19.