基于ALE方法的高速弹体入水冲击特性研究

范旭东，漆 超，王 旭，吕续舰

(南京理工大学 能源与动力工程学院，南京 210094)

高速入水问题广泛存在于空投鱼雷、水雷等各类军事工程应用中.随着海军装备的日益发展，水中兵器，特别是新型反潜武器，在未来海战中将发挥更为重要的作用.此类武器相比空投鱼雷、水雷等射程更远、入水速度相对更高；弹体在高速撞水时会产生巨大的冲击载荷，这种冲击载荷会造成弹体结构及其内部器件的破坏.此外，弹体高速入水瞬间会产生空化效应，使得固-液-气之间发生非常复杂的流固耦合作用，极大地增加了入水载荷和运动特性的评估难度.

对入水过程的研究一直以来都是热点研究对象[1-7].文献[1]探究了不同升角与初始速度对楔形体入水冲击载荷的影响，得到了升角和速度与入水冲击载荷的关系.文献[2]在实验的基础下，采用数值方法对不同落差高度的楔形体入水过程进行了研究，发现楔形体入水高度与升角对楔形体入水冲击期间压力峰值的影响.文献[3]采用显式有限元法对不同曲率的楔形体入水过程进行数值研究，探究了曲率与入水速度对入水冲击载荷的影响.

随着计算机及数值计算方法的发展，通过数值计算的方式进行入水问题的研究开始广泛应用[8-11].在众多数值计算方法中，任意拉格朗日-欧拉算法(arbitrary Lagrange-Euler， ALE)能快速求解瞬时大变形动力学、大变形和多重非线性准静态问题以及复杂的接触碰撞问题，在众多工程实例的应用中取得了较好的效果，具有较高的可靠性.文献[12]采用ALE算法对平板入水进行了数值研究，探究了平板入水过程受到的冲击力.文献[13]通过ALE算法对固定翼飞机水上迫降进行了仿真研究，探究了迫降速度与飞机受力的关系.文献[14]运用ALE方法对自动潜航器入水冲击进行了数值研究，比较了不同初始条件对入水载荷与冲击压力的影响.

目前针对入水问题已经开展了大量的研究，并取得了丰硕的成果，然而对于弹体高速入水的研究相对较少.高速弹体响应迅速可以更快的到达指定区域，对目标进行打击.然而速度的提高也带来了一系列问题，弹体高速入水空化流动更为复杂、更为强烈，入水产生的冲击载荷更大.文中采用ALE算法对不同头型、不同速度的弹体高速垂直入水冲击特性进行研究，分析弹体头型、入水速度和入水角度对弹体入水过程的影响.

1 数值方法

1.1 ALE方法

ALE方法兼具Lagrange方法和 Euler方法二者的特长，在结构边界运动的处理上引进了Lagrange方法的特点，能够有效跟踪物质结构边界的运动；在内部网格的划分上，它吸收了Euler的长处，能够使内部网格单元独立于物质实体而存在，网格可以根据定义的参数在求解过程中适当调整位置，并且网格与网格之间物质也是可以流动的，使得在求解过程中网格不致出现严重的畸变，因此这种方法在分析大变形问题时是非常有利的.

弹体高速入水是强非线性过程，涉及固、液、气三相的运动，采用多介质ALE方法对弹体入水冲击过程进行数值计算.ALE算法的控制方程包括质量、动量和能量守恒方程[15].

1.2 计算模型与网格划分

在ALE方法计算模型中，计算域由空气域、水域和弹体3部分组成，计算采用三维实体建模，对于弹体入水计算模型采用二分之一建模的方法.对于对称面施加对称约束，为了保证可以模拟无限水域与空气域的情况，对空气和水的非对称面边界施加无反射边界条件设置，空气边界与自由液面边界初始状态均为静止的，空气和水的接触采用共节点方法.弹体计算选用拉格朗日实体单元，*MAT_RIGID材料模型，Lagrangian 1号单元算法.空气和水采用的是欧拉实体单元并且采用多物质ALE 11号单元算法.空气和水均选用*MAT_NULL材料模型.

入水计算域和弹体模型如图1.入水弹体总长度L=300 mm，圆柱段直径D=30 mm，弹体质量为1 089.5 g，质心位置距弹头135 mm，弹体材料为45#钢.此外，3种弹体头部空化器直径d分别为30、21.2、15 mm，对应面积与弹身圆柱段横截面积比分别为1∶1、1∶2和1∶4，分别标记为Projectile A (PA)、Projectile B (PB)和Projectile C (PC)，如图1(c).模型采用六面体网格离散空气域和水域，而较为复杂的弹体则采用四面体网格进行离散.

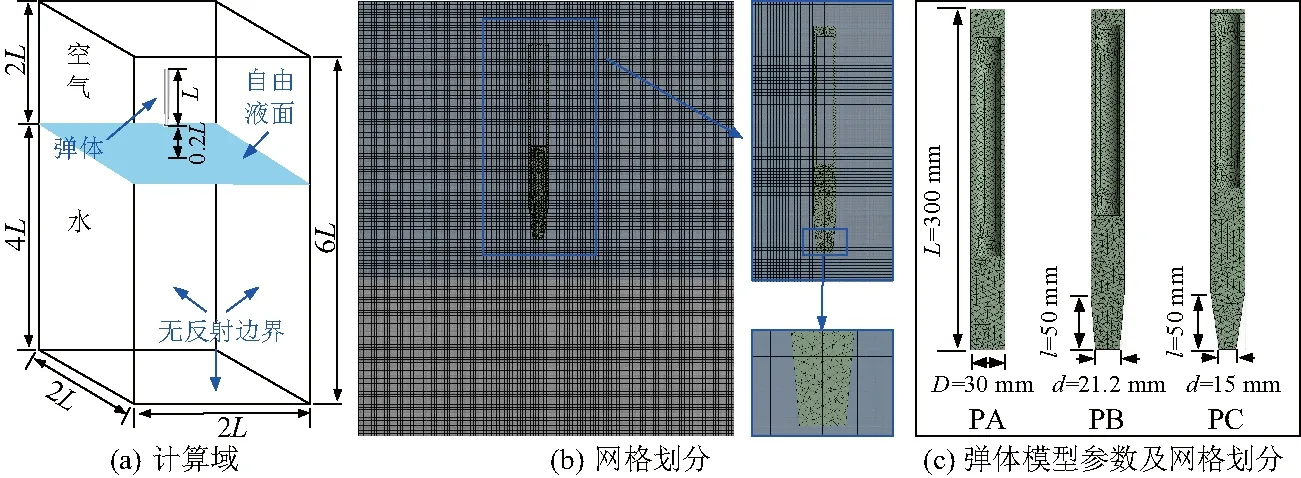
图1 计算域及网格划分

1.3 网格无关性验证

网格尺寸对于计算结果的影响较大，精细的网格能够得到较为精确的计算结果.以PA模型800 m/s入水工况为例，分别选取网格尺寸6 mm(网格数N=150万)、4 mm(N=506万)和2 mm(N=4 050万)尺寸的网格开展入水时间t仿真计算工作，得到入水过程中弹体加速度a变化曲线，如图2.可以看出，当网格尺寸由6 mm减小至4 mm时，弹体加速度峰值变化幅度达到31.2%，进一步缩小网格尺寸至2 mm，峰值仅改变0.2%，入水过程中的弹体加速度变化曲线吻合良好.对比3套网格的计算时间发现，4 mm网格模型计算耗时相较于6 mm模型增加了10.3 h，而2 mm网格模型的计算耗时则在4 mm模型基础上大幅增加，如图3.

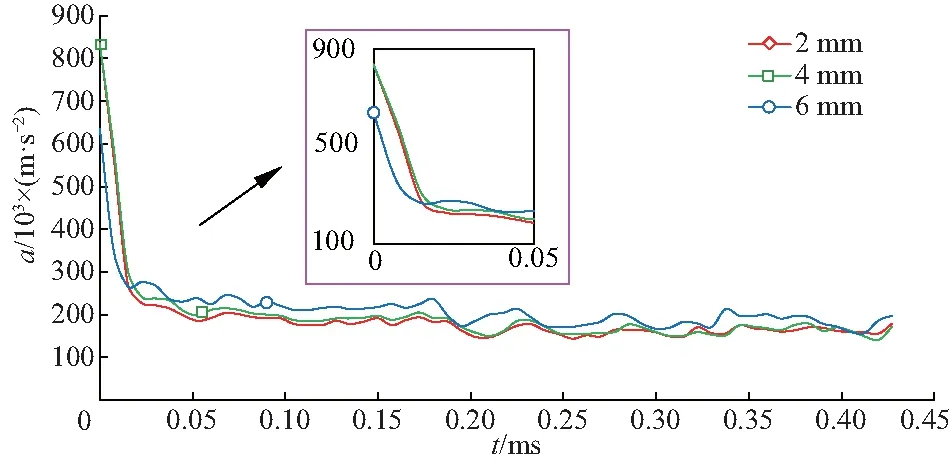
图2 不同网格尺寸下弹体入水加速度变化

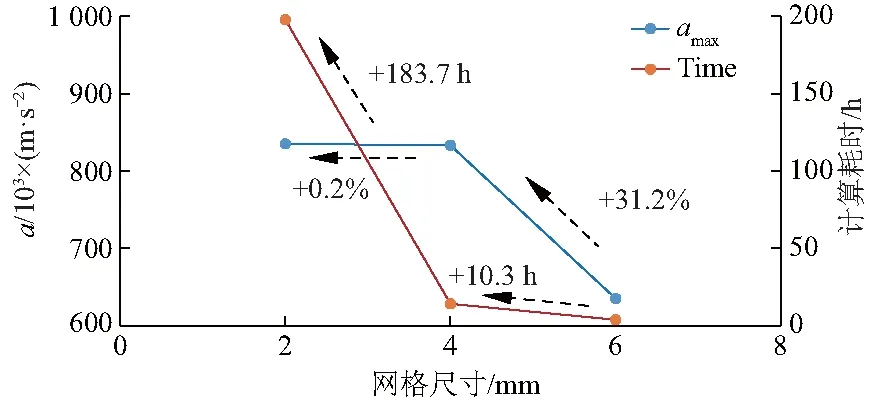
图3 不同网格尺寸下弹体入水最大加速度与计算耗时

综上所述，4 mm网格模型能够兼顾计算效率与计算结果的准确性，而针对PB和PC的入水计算也有同样的规律，因此文中后续均采用4 mm网格开展入水计算研究，计算网格总数约为506万，采用Dell工作站(Intel(R) Xeon(R) CPU E5-2678 v3 @ 2.50GHz 24 核)开展单个工况计算大约耗时21 h.

文献[16]对结构体入水过程进行研究时发现，弹体垂直入水后会很快进入稳定航行阶段，此阶段入水弹体被空泡完全包裹，阻力系数趋于稳定.在建立的入水空泡求解模型中，认为此时结构体入水的动能损失量完全用于排开结构体周围流体并形成空泡，文献[17]在文献[16]的研究基础上由牛顿第二定律得到此时入水结构体的加速度计算公式：

(1)

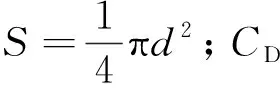
通过分析得到的加速度理论值与文中计算值比较如图4.可以发现入水时间t为0.5 ms后弹体加速度趋于稳定，与理论公式计算得到的加速度(126 104 m/s2)非常接近，即说明文中计算模型对于弹体在水中的运动计算是可靠的.

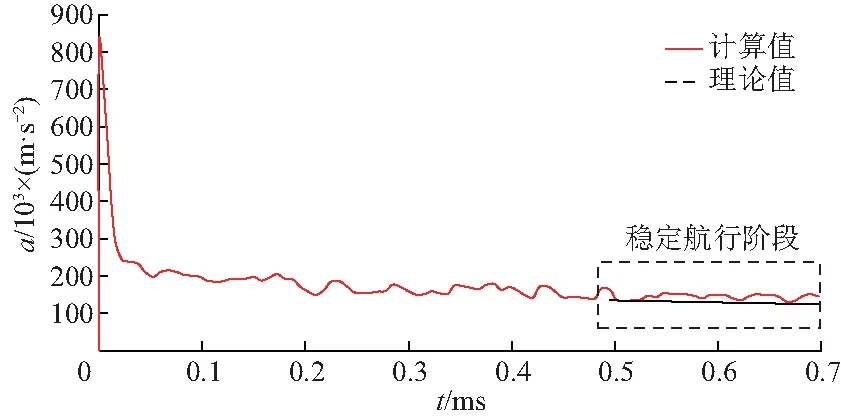
图4 入水加速度曲线比较

文献[19]对物体垂直入水初期的空泡轮廓进行研究并给出了经验公式：

(2)

式中：x和y分别为水平方向和竖直方向坐标.

根据上述入水过程分析，取弹体入水后稳定航行阶段(t=0.5～0.7 ms)的空化轮廓，与经验公式对比，如图5.

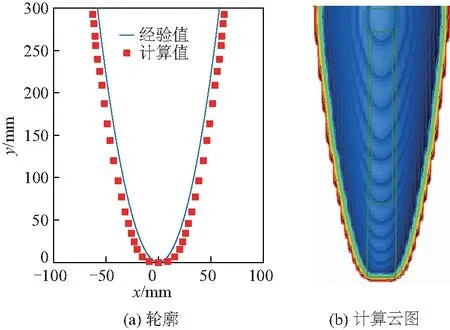
图5 空泡轮廓计算值与经验值对比

可以发现，文中计算与经验公式得到的结果基本一致，进一步证明了文中所建立的计算模型的可靠性.

2 计算结果及分析

为了研究弹体高速入水的冲击特性，针对不同头型和入水速度的弹体开展了高速入水仿真计算研究，对比了不同参数下弹体高速入水冲击特性.

2.1 典型弹体入水冲击特性

图6为PB弹体800 m/s垂直入水过程中流场压力P分布情况，取初始水域压力为零.可以看出，PB弹体砰击自由液面瞬间产生冲击压力，此后以压力波的形式继续向弹体运动方向传播，在水介质的吸收下其能量不断耗散，压力逐渐降低.弹体运动过程中，弹头持续对水产生作用力，并向周围传播形成压力波系.压力波系的大小与弹体运动速度有关，速度越大压力波系的峰值越大.由于弹体砰击水面受到极大的瞬时载荷，因此压力波系的变化较为明显；当弹体入水形成超空泡后，此时弹体速度平稳降低，因而压力变化相对较小.

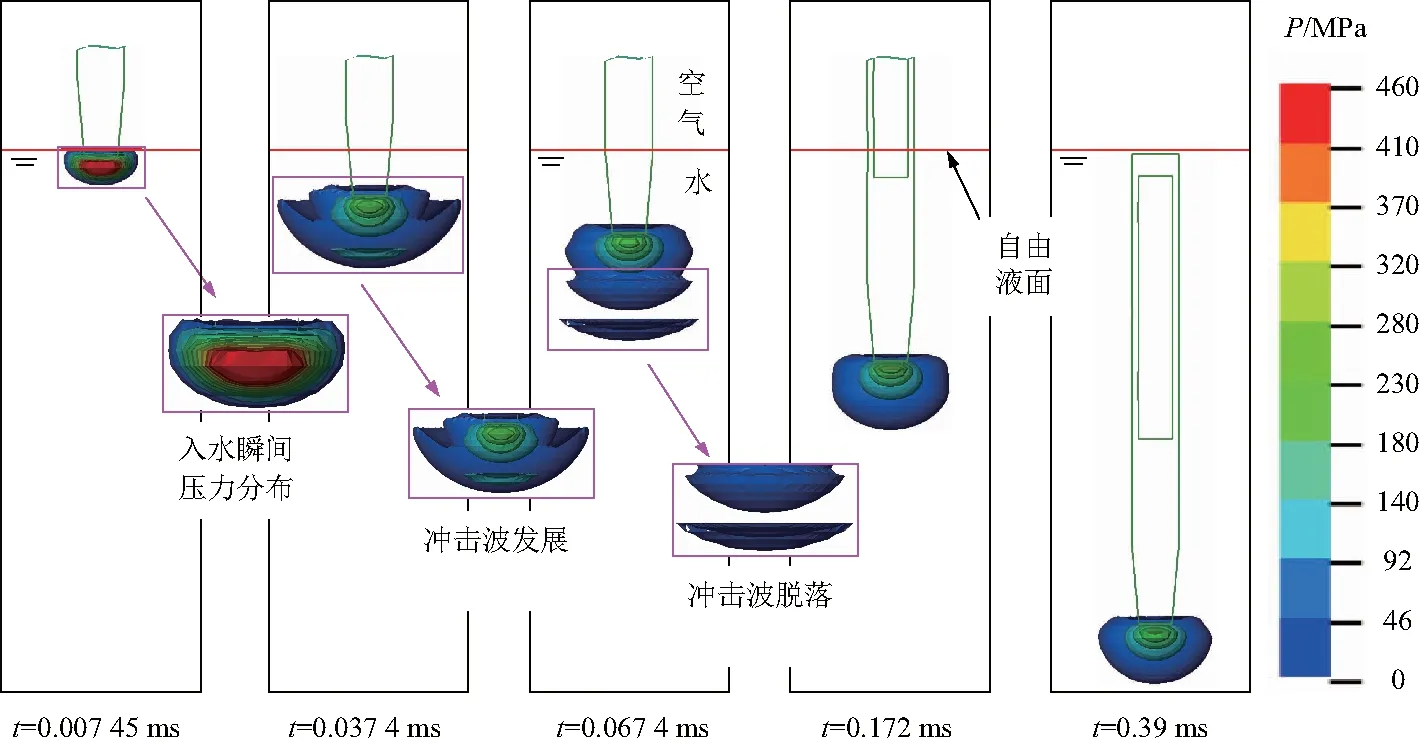
图6 PB弹体入水流场压力分布

弹体高速入水过程中，会伴有超空泡现象的产生.图7为PB弹体在800 m/s入水下的空泡轮廓演化过程.可以看出，当弹体砰击静水面时，弹头与水发生强烈的冲击作用，大量动能瞬间被传递到周围流体中，导致自由液面局部向上隆起，并形成飞溅水花向空气域运动.弹体触水瞬间头部沾湿，流动在弹肩附近发生分离，诱导产生局部空泡.由于空气与水介质间密度差异巨大，弹体周围局部空化后会卷吸大量空气，同时弹体冲击水面入水后持续将自身动能传递给周围流体，在惯性力作用下空泡发生扩张，其长度和直径在一定时间内持续增大，如图7.随着弹体入水过程的进行，其速度在周围水域压力的作用下逐渐降低，空泡扩张的惯性力和水域压力逐渐平衡，此时空泡达到扩张-收缩的临界状态，在距离自由液面深度HC=0.8D处，D为弹体圆柱段直径，达到空泡的最大尺寸DC=3.5D.

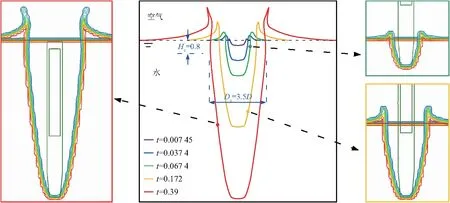
图7 PB弹体入水空泡轮廓演化

图8为入水冲击过程中3个压力监测点上的压力变化情况，分别为距离水面h为0.003L、0.5L和L处，L为弹体总长.可以看出，弹体触水瞬间经历巨大的冲击载荷，测点1的压力脉动峰值达到570.43 MPa，如图8中h=0.003L测点所示.在h=0.5L测点曲线上可以看出，在测点2经历压力峰值前首先出现小幅波动，其原因是弹体撞水后产生的冲击压力向水深方向传播，其传播速度大于弹体运动速度，在弹体到达测点2时再次出现压力脉动，但峰值明显小于测点1.

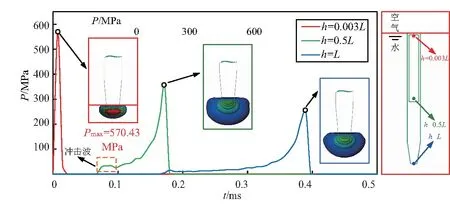
图8 PB弹体入水监测点压力变化曲线

可以看出，随着水域监测单元深度的增加，压力脉动的幅值越来越小，冲击压力传播的范围逐渐减小.

2.2 不同头型弹体入水冲击特性

为研究头型对弹体入水冲击特性影响，对PA、PB和PC 3种头型弹体以速度为800 m/s速度入水冲击过程开展计算研究.图9为不同头型弹体入水空泡轮廓演化情况.可以看出，当入水速度相同时，同一时刻下PA弹体入水空泡直径大于PB弹体和PC弹体，同时自由液面变化更剧烈，溅起更高的水花，进一步表现出弹头空化器面积对空化过程的显著影响，而出现这一现象的原因是随着空化器面积的增加，弹体触水时刻有更大的沾湿面积，从而促成短时间内更多的能量传递到周围流体，使自由液面升高，空泡扩张的惯性作用更明显.此外，通过观察弹头附近空泡轮廓线可以发现，不同头型弹体空化时诱导流动分离的位置有所不同.对于PA弹体而言，流动从弹肩发生分离，而对于PB和PC弹体，由于头部存在锥角，流动分离的位置相对PA弹体有所提高，空化器在浸没一定深度后诱导产生空化.

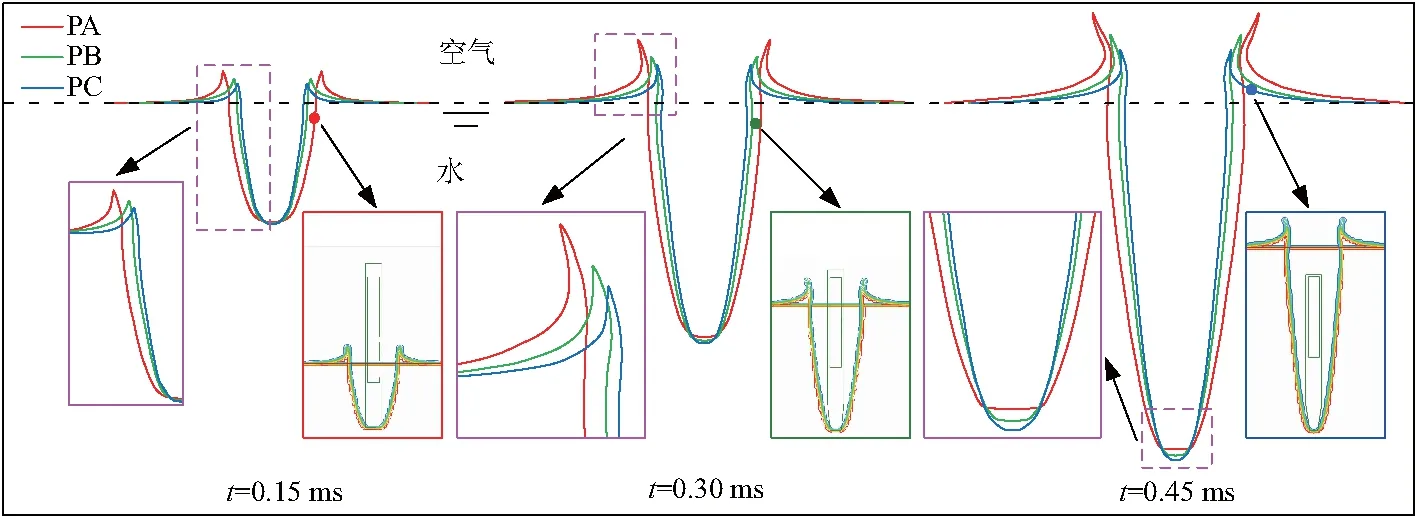
图9 不同头型弹体入水空泡轮廓

图10为PA、PB和PC入水后0.01、0.15 ms时刻的流场压力分布云图.可以看出，在相同入水速度下，弹体入水冲击载荷大小受到空化器面积的直接影响，如图10(a)，PA、PB和PC对应的冲击压力峰值分别为822.13 、570.43、419.02 MPa.当t=0.15 ms，在水域压力的作用下弹体运动速度减小，头部压力峰值和高压区域面积相比入水初期均有明显减小的趋势，但压力峰值和压力扩散区域的面积仍与弹体空化器面积相关，如图10(b).

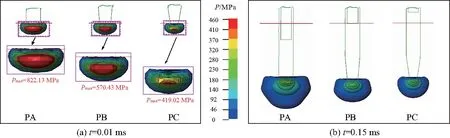
图10 不同头型弹体入水冲击压力特性

图11、12为不同头型弹体入水冲击的加速度a和速度U变化.弹体高速入水瞬间与水发生激烈碰撞，会产生巨大的冲击阻力，此时的入水冲击载荷会远大于其他时刻.能够发现，PA弹体由于空化器面积较大，入水冲击瞬间经历了更为明显的加速度变化，如图11，且稳定入水后所受阻力相对较高.

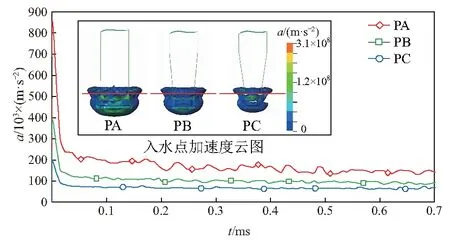
图11 不同头型弹体入水冲击加速度变化曲线

而PB和PC弹体由于空化器面积较小，入水冲击加速度变化幅度相对较小，入水冲击期间引起的速度变化不明显.但由于弹入水过程时间一般为微秒级，因此冲击阻力对弹体的作用时间极短，并且作用面积不大，因而总的相对冲量相对较小，速度降低幅度相比整个运动过程较小，如图12.

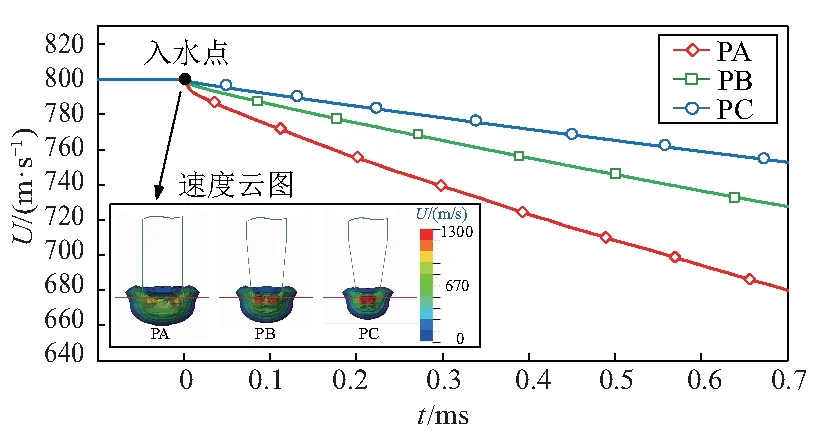
图12 不同头型弹体入水速度变化曲线

图13为PA、PB和PC 3种弹体表面最大压力P随时间变化曲线.弹体入水瞬间，弹体头部与水碰撞，此时监测到的弹体表面压力远远大于入水过程中其他时刻的压力.当速度相同时，3种弹体在入水过程中弹体表面的最大压力分别为PAmax=3.95 GPa，PBmax=3.85 GPa，PCmax=3.90 GPa.通过对比可以发现，三者入水过程中弹体表面最大压力值较为接近.随着弹体入水过程的进行，弹体进入稳定航行阶段后，此时弹体表面压力变化很小.对0.6～0.7 ms弹体表面压力进行分析，发现速度相同时，弹体表面压力大小与弹体头部面积有关，头部面积最大的PA弹体表面压力最小，面积最小的PC弹体表面压力最大.

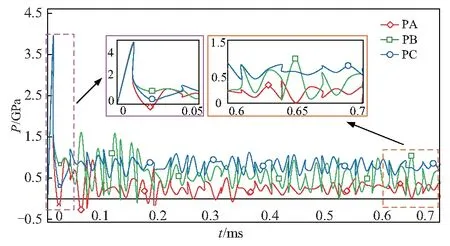
图13 不同头型弹体表面最大压力随时间变化曲线

另外对这段时间的3种弹体所受压力曲线进行直线拟合，得到直线拟合方程分别为PA：P=-0.052t+0.291 5；PB：P=-0.254 3t+0.666 2；PC：P=-0.377t+1.029 2(单位为GPa).通过对比直线拟合方程发现，在此阶段压力下降幅度随弹体头部面积而变化，头部面积最小的PC压力下降最快，而面积最大的PA则下降的最慢.

图14为不同头型弹体入水冲击的结构响应云图.弹体入水瞬间弹体的结构响应如图14(a)，弹体高速入水瞬间与水发生激烈碰撞，会产生巨大的冲击阻力，此时的入水冲击载荷会远大于其他时刻.可以发现，冲击载荷主要作用于弹体的头部， PA弹体由于空化器面积较大，能够起到很好地缓冲作用，冲击载荷分布更为分散，而PC弹体由于空化器面积较小，冲击载荷分布更为集中，弹体头部在入水瞬间更容易被破坏.图 14(b)为弹体完全进入水中时的结构响应云图，此时弹体整体被超空泡所包裹进入稳定航行阶段，此阶段弹体表面的压力相对较小，入水阻力大小稳定.由此得出，在相同的入水速度下，弹体高速入水冲击过程中入水瞬间弹体头部更容易被破坏，并且弹体头部空化器面积越小越容易被破坏.

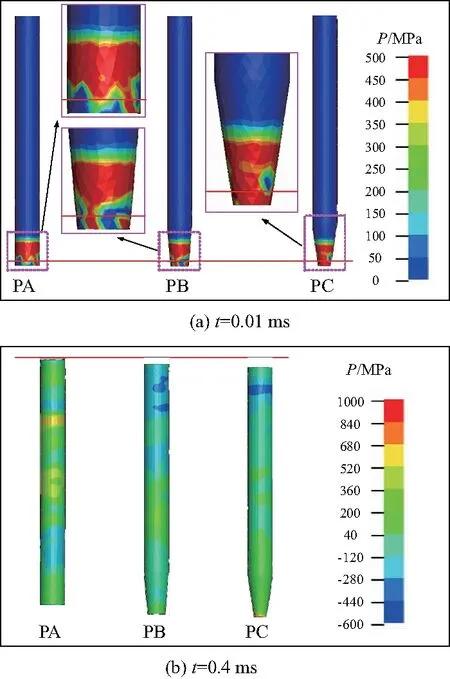
图14 不同头型弹体结构响应云图

2.3 不同速度下弹体入水冲击特性

图15为PB弹体不同速度下入水冲击自由液面的流场压力分布情况.能够发现，弹体撞水瞬间(t=0.01 ms)头部出现高压，且压力峰值和压力波传播范围随着弹体速度的增大有明显提高，在速度为600、800、1 000 m/s时，对应的压力峰值分别为413.75、570.43、668.32 MPa，如图15(a).随着弹体入水运动的进行，由于弹体的运动速度降低，弹体头部压力逐渐减小，但仍遵循压力分布与弹体运动速度呈正比的关系，如图15(b).而对PA弹体在800 m/s速度下入水压力场计算中发现，其撞水后流场最大压强为822.13 MPa，大于PB弹体在1 000 m/s速度入水所能达到的压力峰值，由此发现在800～1 000 m/s的速度范围内，弹体空化器面积对入水冲击压力特性的影响大于入水速度的影响.

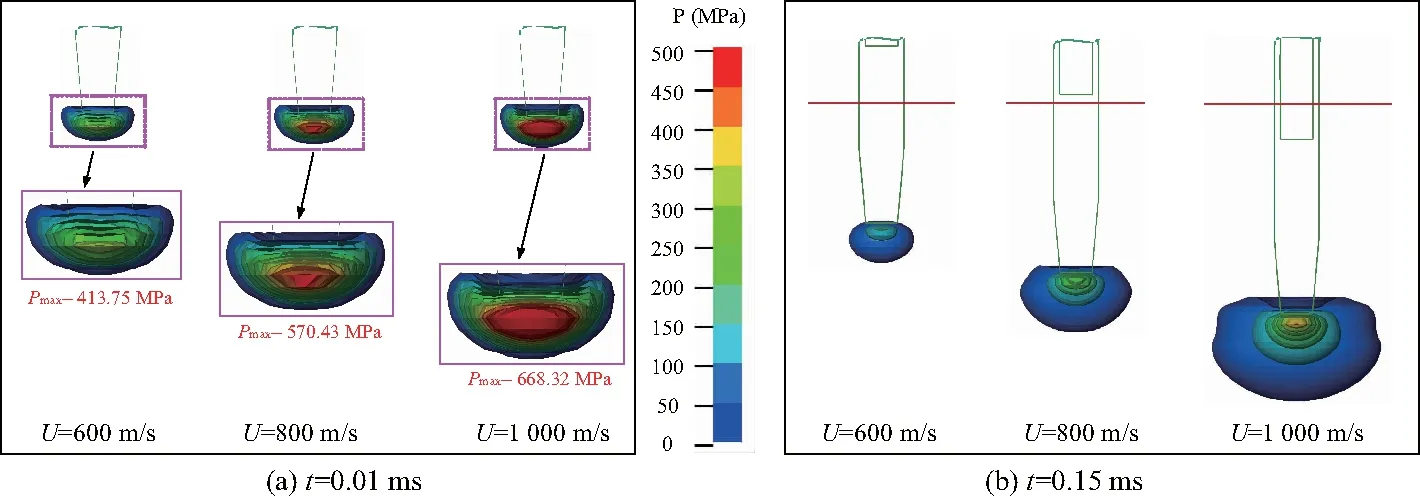
图15 不同速度下PB弹体入水流场压力分布特性

当弹体以不同速度入水时，由图16(a)发现相同时刻弹体入水产生的空泡大小与弹体速度有关，当弹体以较高速度撞水时，所能传递给周围流体的动能相对较高，从而使空化过程中空泡扩张惯性力较大，使空泡达到扩张-收缩的临界时间延后，形成较大的空泡同时溅起更高的水花.而通过对比相同深度下的空泡轮廓发现，当弹体外形相同时，不同入水速度下形成的空泡轮廓仅有微小差别，如图16(b).这一发现与文献[22]研究发现的弹体入水初期的空泡轮廓经验公式(式2)基本吻合，即影响空泡轮廓的决定性因素为弹体头部直径，而当弹体外形参数确定时，式中仅有阻力系数CD影响空泡轮廓大小，而CD是与速度成正比的不敏感阻力系数，随着速度的增大阻力系数也会小幅增加，图16(b)很好地反映了这一现象.

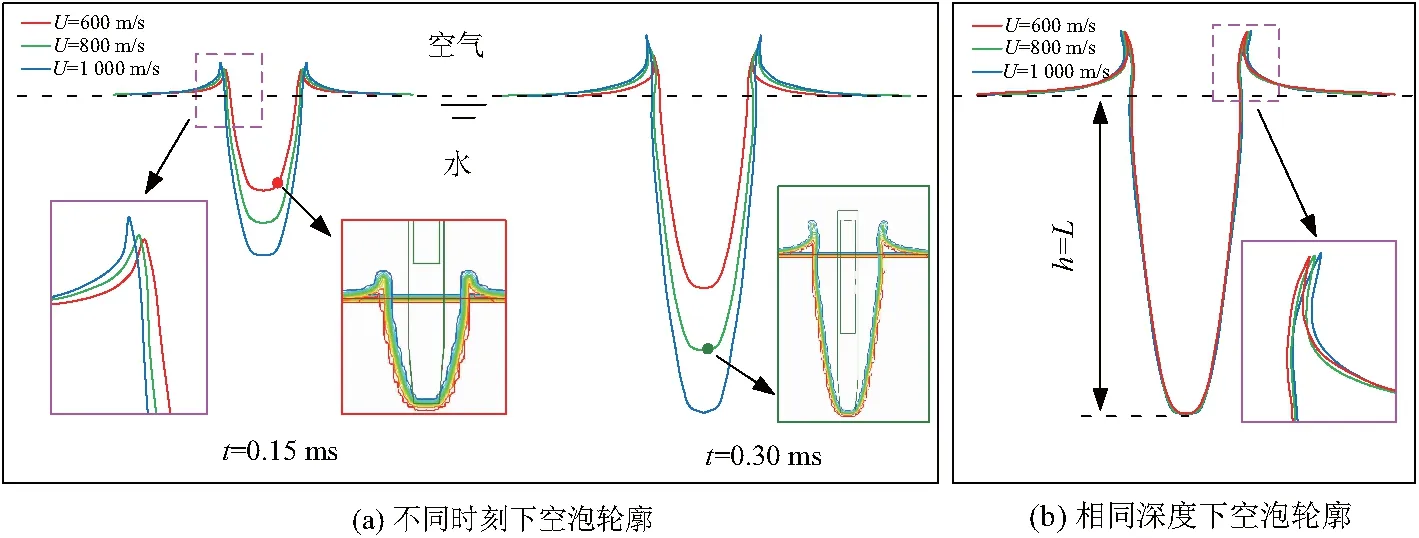
图16 不同速度下PB弹体入水过程空泡演化特性

图17～18为初始速度U0下PB弹体入水过程中的速度和加速度变化曲线，U/U0为反映速度变化的速度比.弹体入水瞬间，由于头部与水发生强烈碰撞，弹体速度会在极短的时间内突降，但降低幅度相较于整个入水过程是小值，周围流体速度会急剧增加，可以发现弹体入水速度越大，入水过程中速度下降越快.入水瞬间产生的冲击载荷越大，入水加速度的最大值分别为180 490 、378 000、567 764 m/s2.虽然这一入水加速度数值相对于整个入水过程是最大的，但弹体入水过程中弹体头部与水接触是一个极其短暂的过程，因此冲击阻力对弹体的作用时间极短，并且作用面积不大，因而总冲量相对较小(冲量公式I=Ft，式中：I为冲量；F为冲击阻力；t为作用时间).此后弹体加速度平稳降低，速度以接近线性变化的方式减小.

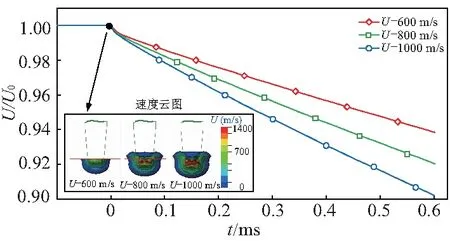
图17 不同速度下PB弹体入水速度变化对比

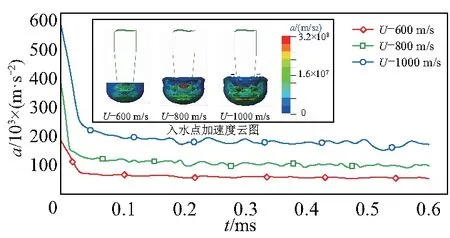
图18 不同速度下PB弹体入水加速度变化对比

3 结论

(1) 采用ALE方法对PA弹体高速入水过程开展仿真计算，获得了弹体入水冲击特性、压力传播特性及空泡轮廓演化过程等，与相关理论研究结果取得较好的一致性.

(2) 针对不同头型弹体的入水计算研究表明，在相同入水速度下，当弹体空化器面积较大时，入水过程具有较高的冲击压力，入水速度衰减较快，空泡扩张程度较大，但不同头型弹体入水后弹身的压力值较为接近，因此需要考虑实际需求，综合评估弹体头部材料与冲击特性、减阻性能以及弹体头型间的关联.

(3) 当弹体以不同速度入水时，入水速度越大，弹体撞水对自由液面的冲击压力峰值越高，压力波传播范围越大.然而在文中研究所考虑的速度范围中，相同深度下，入水速度对空泡轮廓影响相对较小，受弹体空化器面积的影响较大.