磁悬浮平面电机及其自适应收缩反步控制
杨冠军,王伟然,2*,闫景昊,葛慧林,智鹏飞
(1.江苏科技大学 电子信息学院,镇江 212100) (2. 南京航空航天大学 自动化学院,南京 211106)
现代物流在地区经济发展中发挥着重要作用,随着现代化和智能化技术的发展,物流传送技术也发生着变革.磁悬浮平面电机(magnetic levitation planar motor,MLPM)具有无摩擦损耗、动态响应快速等优点,由其组合而成物流传送装置具有Celluveyor的特点,而且速度更快、能耗更低.该装置中每一个磁悬浮平面电机即为一个单元模块,通过对模块的任意组合可以实现不同工况下的运输要求,这种模块化、分散集成的新型物流系统也是现代化物流传送技术发展的方向.
应用于物流传送领域的MLPM,对其控制的快速性及稳定性有着较高的要求.文献[1]将常规PID控制算法应用于磁悬浮控制,系统响应速度并不理想,浮子不能实现快速悬浮,此外系统鲁棒性也较差,当内部参数摄动或受到外界干扰时,系统状态会与平衡点发生较大偏离.文献[2]利用自抗扰控制(active disturbance rejection control,ADRC)对系统的综合扰动进行估计,并及时对系统进行补偿,相比PID控制,ADRC在较宽的速度范围内具有良好的动态性与鲁棒性.文献[3]将线性化反馈鲁棒控制引入电磁悬浮系统,可以保证系统的稳定性,但系统瞬态响应中有较大的超调与振荡,导致其难以应用于磁悬浮装置的实时控制.文献[4]将磁悬浮系统在平衡点处线性化,并设计了具有积分型滑模面的自适应滑模控制器,实现了磁悬浮系统对方波及正弦波信号的跟踪.
上述方法难以满足时变条件下物流传送系统动态与稳态性能的要求.反步设计方法[5]是一种系统辨识求模型的方法,具有很好的快速性,理想情况下没有超调量,同时满足系统动态性要求.此外,反步控制与收缩控制的融合,无需将系统在平衡点线性化,有助于解决系统参数不明确时的建模问题.
文中建立磁悬浮平面电机推力及转矩模型,实现六自由度的控制量解耦.通过对磁浮托盘动子的受力特性分析,考虑模型不确定参数及外部负载扰动建立磁悬浮平面电机六自由度运动系统的解耦控制模型.设计了一种针对于MLPM解耦模型的自适应收缩反步(adaptive contraction backstepping,ACB)控制器,该方法无需在平衡点处线性化系统,即可完成对磁悬浮平面电机的自适应运动控制.结果表明这种方法具有理想的响应速度、较强的鲁棒性与良好的动态跟踪能力.
1 磁悬浮平面电机的结构与系统建模
1.1 磁悬浮平面电机原理
圈式MLPM由定子和浮子两部分构成,结构如图1,浮子为动圈式结构,由4个线圈组组成.每个线圈组由3个线圈组合而成.二维Halbach型永磁阵列可以提供三维分布的空间磁场,二维Halbach磁阵列由主磁钢和副磁钢组成,主磁钢为正方形,副磁钢为矩形,其磁化方向均平行于水平面,主磁钢与副磁钢厚度相同,充磁强度相同,且均匀磁化.磁场中的通电线圈可以同时产生竖直与水平方向的电磁力,从而提供磁悬浮平面电机浮子运行过程中的悬浮力和驱动力[6].
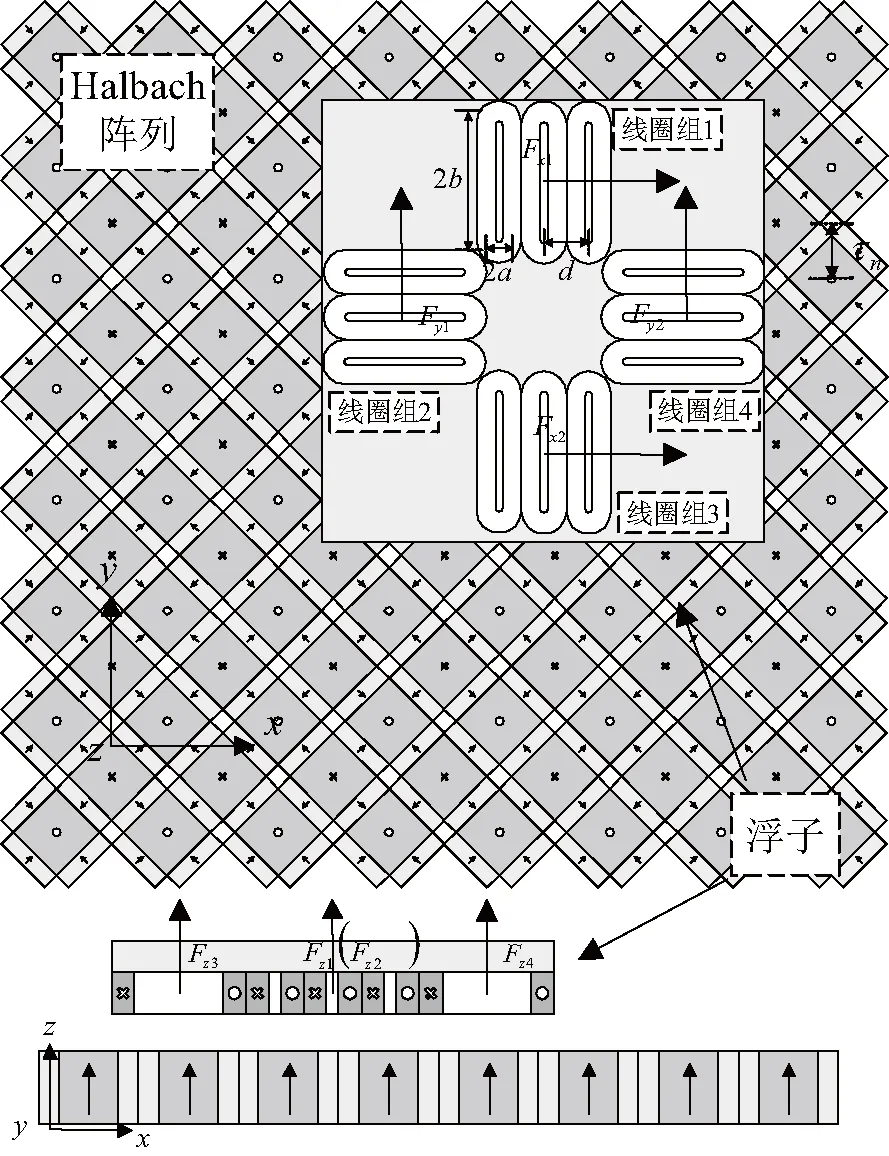
图1 磁悬浮平面电机结构
图1中,线圈的宽度长度定义为2a、2b,Halbach磁阵列的极距记为τn,线圈组中两邻近线圈的中心距,记为d,以逆时针的顺序定义4个线圈组的组号为1、2、3、4.线圈组产生的推力记为Fx1、Fx2、Fy1、Fy2、Fz1、Fz2、Fz3、Fz4.
1.2 磁悬浮平面电机的数学模型
以线圈组作为MLPM的基本驱动单元建立MLPM的数学模型,Halbach型永磁阵列空间磁感应强度B具有如下分布:
(1)
式中:Bx、By和Bz为沿x、y、z3个方向的磁通分量;B0为当z=0时磁通密度的一次谐波的有效幅值;τn为两相邻同向磁钢中心距的一半定义为极距.已知磁感应强度的空间分布和线圈的形状尺寸,由洛伦兹力公式计算其推力及转矩为:
(2)
式中:JV为线圈面电流密度;B为磁感应强度;r为体积微元对应的力臂;V为线圈体积.以线圈组1为例,其在Halbach型永磁阵列中受到的推力,可描述为:
(3)
式中:Fx1、Fy1、Fz1为线圈组1的推力,KFx为考虑到线圈直径厚度特征尺寸等因素的推力影响系数;d为两邻近线圈的中心距.线圈组相对于质心转矩用来提供偏转时所需的控制力从而实现多自由度控制,关于通电线圈在Halbach型永磁阵列中的转矩,可描述为:
(4)
(5)
(6)
式中:Tx1、Ty1、Tz1为线圈组1的转矩;KTx,KTa为考虑到线圈直径厚度特征尺寸等因素的转矩影响系数.
2 磁悬浮平面电机的力/电流模型
如图1线圈组1、3提供x向推力分量,线圈组2、4提供y向推力分量,4个线圈组均可提供z轴竖直方向推力分量.浮子的线圈组作为驱动整体,z轴合力为Fz=Fz1+Fz2+Fz3+Fz4,x轴与y轴合力为Fx=Fx1+Fx2,Fy=Fy1+Fy2,线圈转矩为Tz=-lx1Fx1-ly2Fy2+lx3Fx3+ly4Fy4,Tx=lx1Fx1+lx2Fx2-lx3Fx3-lx4Fx4,Ty=-ly1Fy1+ly2Fy2+ly3Fy3-ly4Fy4.其中Fx,Fy,Fz,Tx,Ty,Tz是整个浮子受到的推力和转矩,lx、ly为各推力分量作用点到浮子质心的x向力臂和y向力臂.
确定线圈组的推力分配方式后,给各线圈施加电流来获得所需大小的推力分量.电流分配方式与两个参数有关,一是该线圈组包含的线圈个数,记为N,二是线圈组中两邻近线圈的中心距d.x轴方向与y轴方向的力/电流模型原理相同,仅电磁力方向有所差异,因此只以x轴为例进行说明.
如图2,设线圈组中的中心线圈中心位置坐标为(xc,yc,zc),并以此来表征线圈组在全局坐标系中的位置.包含N个线圈的线圈组1,N为奇数.线圈组中各线圈的位置坐标分别为(xc,yc,zc)、(xc+d,yc,zc)和(xc+(N-1)d,yc,zc).
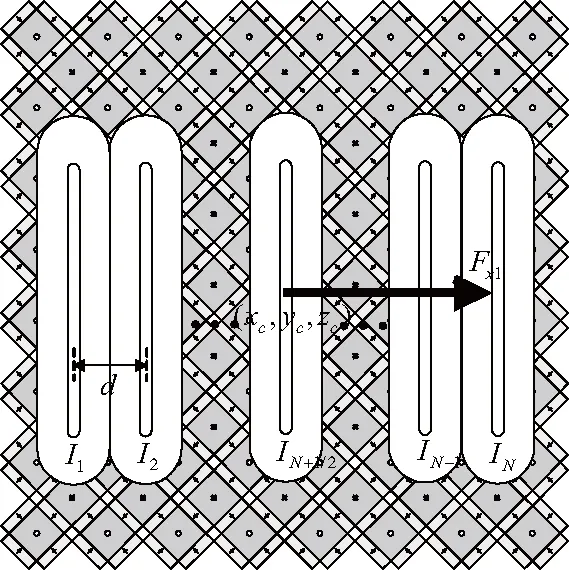
图2 线圈组结构示意图
式中:I1、I2和IN分别为线圈组中线圈实际通入的电流,幅值均相同.Fx1与Fz1是此线圈组提供的x与z轴的推力分量.Q为矩阵:
推力所需的等效电流矩阵为:
(8)
式中:Iq和Id分别为提供水平推力分量和竖直推力分量所需的等效电流,一般将Iq称为交轴电流,将Id称为直轴电流.取d为4τn/3,则三线圈相位正交时,可以保证各线圈组提供的推力分量达到最大值.因此线圈组的电流分配方式为:
当线圈组1仅产生沿x水平方向的推力时
(9)
式中:I1、I2和IN分别为线圈组中线圈通入的电流.则线圈组1产生沿x轴水平方向推力Fx1,线圈组1所受分布力产生的绕y轴的转矩Ty1和绕z轴的转矩Tz1均不为零.
线圈组1仅产生沿z轴垂直方向悬浮力时
(10)
则线圈组1产生的沿z轴垂直方向悬浮力Fz1,线圈组1所受分布力产生的绕x轴的转矩Tx1和绕y轴的转矩Ty1均不为零.
另外,如果令线圈组1、3沿x、y轴水平方向的推力大小相等,方向相反,相互抵消,两组线圈组所产生绕x、y轴的转矩为零,绕z轴的转矩相同,相互叠加,此时动子仅产生绕z轴的转矩;令线圈组1、3沿y、z轴垂直方向悬浮力大小相等,方向相反,相互抵消,两组线圈组所产生绕y、z轴的转矩为零.绕x轴的转矩相同,相互叠加,此时动子仅产生绕x轴的转矩.
3 磁悬浮平面电机的自适应收缩反步控制
3.1 磁悬浮平面电机的动力学模型
MLPM浮子受到的作用力除重力外还包括永磁阵列与浮子线圈之间的电磁推力,将其刚性扰动归结为负载的变化,将其柔性扰动归结为阻尼项[7],扰动力可以通过运动控制器来抑制,在建立MLPM动力学模型的过程中,仅考虑重力与电磁力对系统的影响,其动力学模型为:
(11)
式中:Fx、Fy、Fz为推力;Tx、Ty、Tz为电磁转矩;hx、hy、hz、htx、hty、htz为刚性扰动产生的负载力;m为浮子质量;Jx、Jy和Jz为浮子绕各转轴的转动惯量;x、y、z为浮子沿各方向的平动位移;θx、θy、θz为浮子绕各转轴的转角位移,g表示重力加速度.
结合MLPM的动力学模型与式(3~6)建立磁悬浮平面电机运动系统的动力学方程为:
(12)
式中:KF=KFx·B0为线圈长边推力系数与永磁阵列表面磁感应强度分布幅值B0的乘积;zc为MLPM浮子的气隙高度,即竖直方向位移.IFx、IFy、IFz、ITx、ITy、ITz为竖直各方向运动控制器输出的控制电流,由位置伺服控制算法确定,其与Iq、Id的解耦关系式由文献[8]给出;l为线圈长度,需要按照相应的电流分配方法计算出其在各线圈上的分量,并直轴、交轴电流分量一同施加给各个线圈;r1q1、r2q2、r3q3、r4q4、r5q5、r6q6为干扰项及不确定参数.磁悬浮MLPM运动系统x、y、z、θx、θy、θz6个自由度的运动均可视为双积分环节.
3.2 MLPM的自适应收缩反步控制器设计
从动力学方程式(12)可以看出,MLPM的x、y、z轴位移控制以及对θx、θy、θz的控制是完全解耦的.以z轴为例进行反步设计,基本思想是从原系统选取合适的状态变量分解为新的子系统,然后为每一个子系统设计虚拟控制律,逐步设计最终得到系统的实际控制律,使整个系统达到期望的性能[9].
3.2.1 收缩反步控制器设计
根据式(12)中z轴动力学方程
(13)
式中:c为系数4KF/m;η为与z轴高度相关的exp(-π·zc/τn);u为控制器输入;ρ为一般常量g.
(14)
状态x1的轨迹随时间的指数收敛性用虚拟位移分析,虚拟位移表示空间中同一时刻两个点之间的线性微小增量,记作δx1,在式(14)中引入虚拟位移,第一个子系统的虚拟位移可表示为:
(15)
其中雅可比矩阵参数可表示为:
(16)
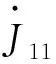
(17)
因此跟踪误差的微分形式可写为:
(18)
(2) 对辅助变量xs求导后将式(16,17)代入可得:
(19)
对于收缩反步控制系统,式(18,19)的虚拟位移状态空间形式为:
(20)
(3) 为了保证xs能够收缩,则实际的控制量u可设计为:
(21)
将控制量u代入(18)通过调节参数使矩阵特征值λmax负定,μ(J)≤-a<0,因此式(21)是增量稳定的,系统收缩至期望轨迹[11].
3.2.2 自适应收缩反步控制器设计
在实际应用中,磁悬浮平面电机的负载扰动与系统的不确定参数不能忽略,因此将其归类为干扰项,在控制率中加入自适应项予以消除[12].
(1) 考虑包含干扰项及不确定参数下的动力学模型为:
(22)
式中:r为不确定参数;q为光滑有界函数.
(2) 考虑xt为包含不确定参数的误差实际值,表示为:
(23)
(3) 在收缩反步法的基础上,设计自适应控制器,即:
(24)
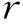
(25)
式中:xs被认为是接近于0的误差参考值,于是有q-1(xt-xs)=q-1xt,设xs=0,可构造自适应系统为:
(26)
因此可通过调节参数使∂f(xt,t)/∂xt=-k2收缩,xt指数收敛至0,且γ有界.由此可知,控制系统是稳定的.并且通过选取k1,k2可以使系统获得较好的快速性与稳定性.
最后,由z轴推导的带有不确定参数的MLPM系统模型为:
(27)
将状态变量推广到x、y、z轴输入控制以及对θx、θy、θz的控制[13-14],令
[x1,x2,x3,x4,x5,x6]T=[x,y,z,θx,θy,θz]T
定义控制量为:
不确定参数更新为:
最终,考虑到应用于物流装置的包含不确定参数磁悬浮平面电机非线性运动模型,文中设计的自适应收缩反步(ACB)控制器可描述为:

(28)
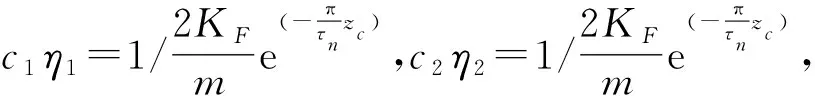
4 仿真与实验验证
为了验证自适应收缩反步控制器的正确性,分别在Matlab/Simulink软件与实验平台进行验证[15],为了模拟启动过程,将磁悬浮平面电机z轴初始状态设置为0,z轴稳定高度设置为固定高度5 mm,对于x轴以及转角的姿态期望轨迹,由于控制的相似性,仅对x轴的水平运动与转角运动进行验证[16].图3是MLPM的z向闭环控制模型.实验平台的参数如表1.
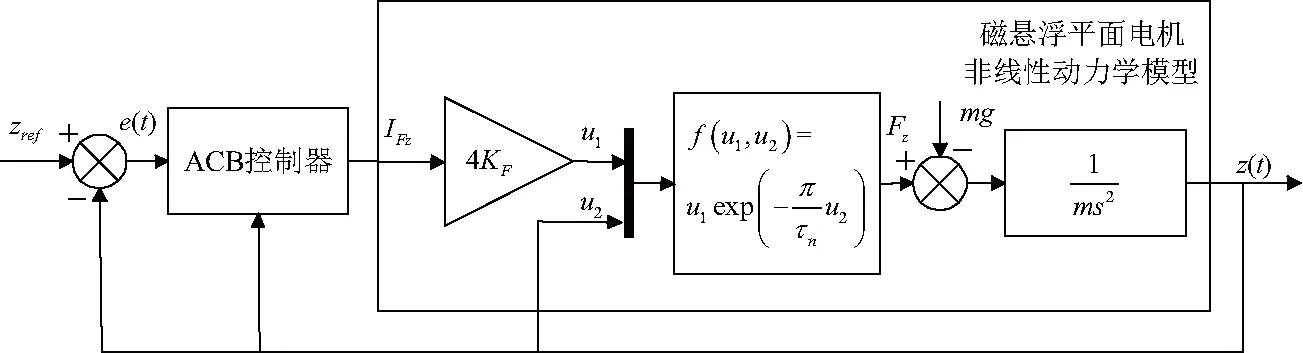
图3 基于自适应收缩反步控制器的磁悬浮控制系

表1 磁悬浮平面电机参数
平面点电机仿真实验如图4、5.由图4、5可以看出,在MLPM模型参数不确定的情况下,传统PID控制器的稳定时间为0.004 3 s并且超调量达到23.9%,ACB控制器的稳定时间为0.002 5 s最终稳定在5 mm并且没有静差与超调量.
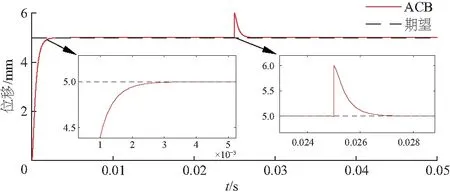
图4 ACB控制z轴高度
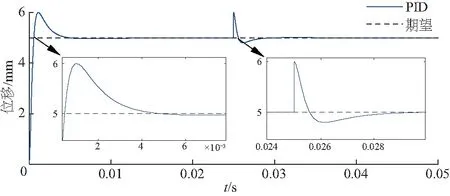
图5 传统PID控制z轴高度
即使修正PID控制器参数使系统稳定时间缩短与ACB控制器一致,但是PID控制器不能抑制系统超调量,新的参数下超调量增长至25.7%,比原参数上升1.8%.0.025 s时系统受到10%的外部扰动,波动为1 mm,传统PID控制器经过0.002 s稳定,而ACB控制器仅用0.001 5 s稳定,其控制性能接近于理想的反步控制,如图6.
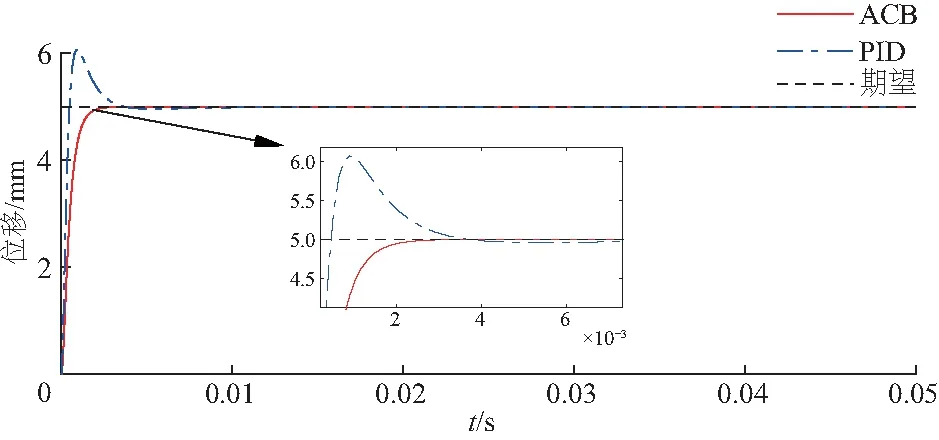
图6 ACB与PID控制z轴对比
因此,采用ACB控制算法时MLPM的启动迅速,能够跟踪期望轨迹的状态,且变化保持在很小的范围内,0.025 s出现扰动时,系统具有良好的抗扰动能力,而PID控制算法效果一般,具有一定的超调量、响应速度也与ACB算法有差距.
由图7,传统PID控制器针对x轴位移与转动弧度的超调量分别为24.8%,28%,稳定时间分别为0.003 5 s,0.004 s,ACB控制器的稳定时间分别为0.002 s,0.018 s最终稳定在5 mm与1.5 rad.ACB控制器有更好的跟踪性能,可以使x轴轨迹紧跟期望轨迹,其控制性能接近于理想的反步控制,并且保留了系统的非线性,自适应项对系统的不确定参数也有很好的抑制作用.传统的PID控制跟踪性不及本文设计的ACB,稳定性较差.
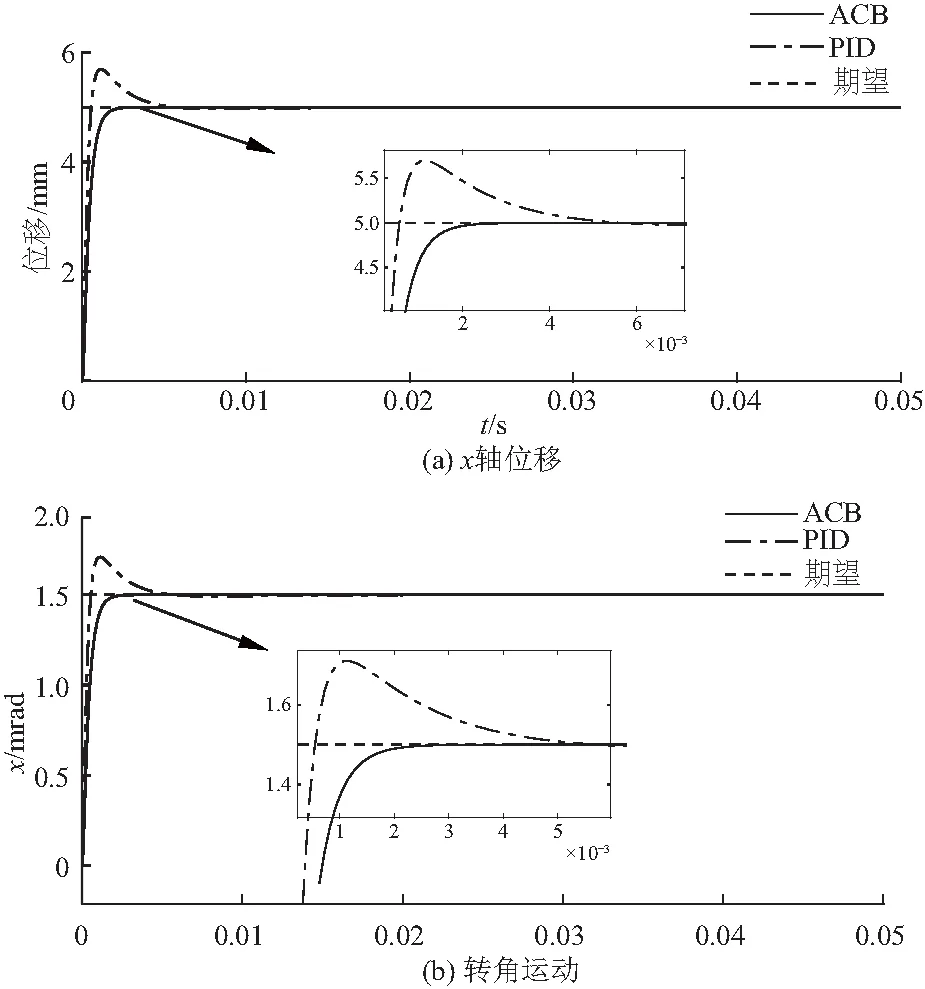
图7 ACB控制x轴位移与转角运动
在仿真环境下,验证磁悬浮平面电机系统的预设轨迹输出性能,其三维空间内的浮子运动轨迹如图8、9.
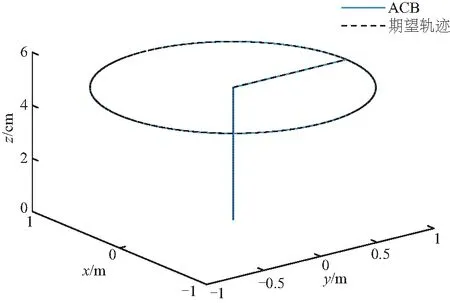
图8 圆形运动三维轨迹
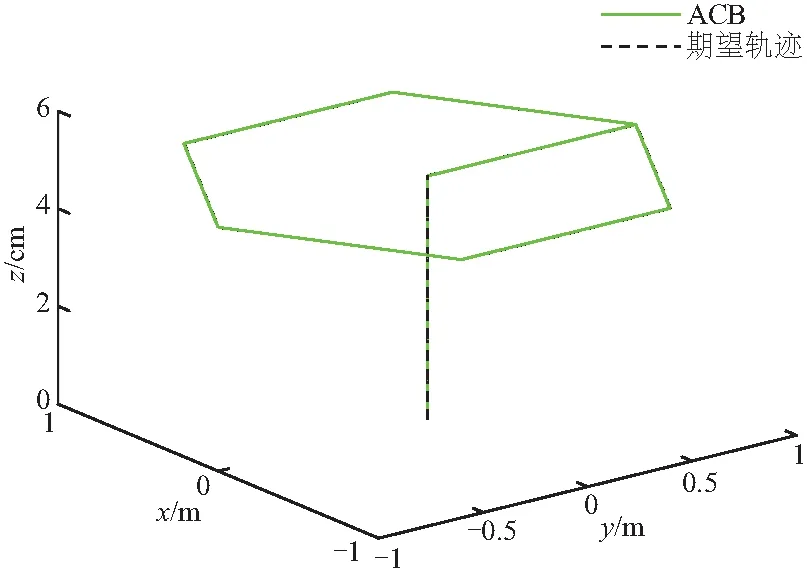
图9 六边形运动三维轨迹
图8中预设轨迹为圆形,从图8可以看出,ACB控制对圆形轨迹具有优异的轨迹输出效果.图9中预设轨迹为正六边形,从图9可以看出ACB控制效果依旧良好.
搭建系统原理性实验验证平台如图10,在浮子上安装高精度的MEMS传感器来测量其实际运动轨迹.实验平台中使用MPU9250,16位数据精度,实时采集x轴向和y轴向的加速度数据,经过数据滤波与位移换算后反馈给示波器.

图10 MLPM线圈组与实验平台
磁悬浮平面电机按照圆形轨迹运动如图11,图中Sx、Sy为x轴和y轴的位移,横坐标与纵坐标每格均表示位移0.3 m.
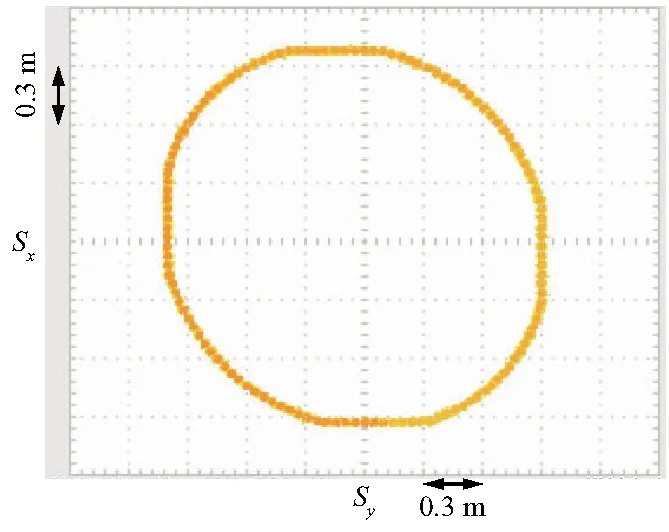
图11 磁悬浮平面电机圆形运动轨迹输出
图12是将其运动轨迹分解至x轴和y轴,横坐标每格表示1 s,纵坐标每格表示位移0.625 m.
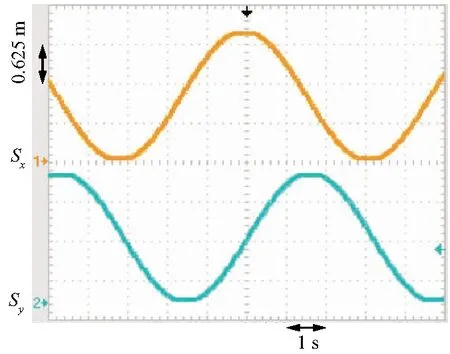
图12 圆形运动轨迹的分解输出
为测试磁悬浮平面电机浮子的折角转弯性能,浮子按照正六边形轨迹运动如图13,图14是将其运动轨迹分解至x轴和y轴,图中横坐标和纵坐标参数与图11、12相同.
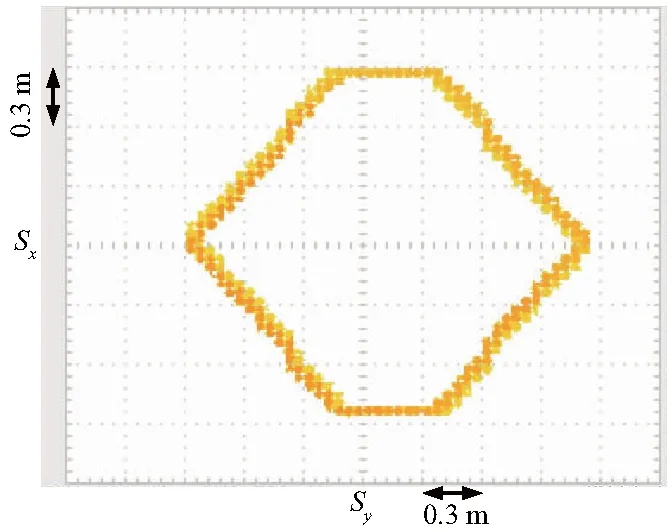
图13 磁悬浮平面电机六边形运动轨迹输出
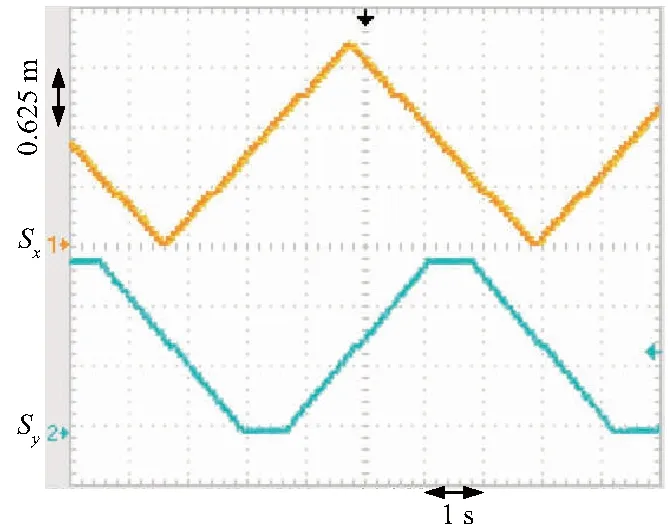
图14 六边形运动轨迹的分解输出
由实验结果可见,浮子大约在6 s内就能完成一次周长为6.283 m的圆周运动,从x轴和y轴的运动轨迹分解输出来看,浮子移动2 m的距离仅需要3 s,速度约为0.6 m/s,动态响应能力优越,并且输出预设轨迹的能力良好.同样在折角转弯实验中,浮子大约在6 s内完成一次六边形轨迹运动,其转弯过程迅速、稳定、基本没有超调.终上所述,磁悬浮平面电机浮子控制实验证明了该装置具有理想的响应速度、较强的鲁棒性与较好的动态跟踪性能,应用在物流传送系统中,并具有较好的效果.
5 结论
文中将磁悬浮平面电机应用于物流传送领域,以磁悬浮平面电机模型为对象,针对其建模与控制方面做出了几点研究:
(1) 分析MLPM的推力、转矩的数学模型,并得到线圈组电流的分配策略,即力/电流模型.
(2) 针对线性系统的特点以收缩理论为核心设计自适应控制器,将不确定参数的实际值与估计值误差限定在满足收缩特性区域内.
(3) 实验与传统PID控制对比实验表明:基于收缩理论的增量稳定分析使得控制系统摆脱了对平衡点的依赖性,同时证明了其在模型参数不确定情况下的鲁棒性,为磁悬浮平面电机在物流方面的进一步应用提供了新思路.

