圆柱体落水过程多相流体动力特性数值分析

王 聪，夏维学，陈超倩

(1. 哈尔滨工业大学航天学院，哈尔滨 150001；2. 海军工程大学兵器工程系，武汉 430033；3. 西北机电工程研究所，咸阳 712099)

0 引言

运动体落水广泛存在于海洋工程、航空航天和日常生活，如船舶撞击、鱼雷入水、飞机水上迫降、滑跳等。本文采用数值方法开展具有初始倾角的圆柱体落水过程多相流动特性和多自由度运动特性研究。

针对运动体落水问题的研究最早见于19世纪末，Worthington[1]针对不同参数的球体、液滴垂直下落撞击自由液面落水的实验研究，分析了落水参数对空泡、水面波纹、回射流水柱、液滴反弹等现象的影响。运动体抨击自由液面瞬间受到瞬时抨击载荷作用[2-3]，该抨击载荷可能导致运动体结构破坏，内部仪器设备失效等问题。为了解决落水撞击问题，May等[4-9]较为系统地研究了小球落水撞击、空泡生成、空泡闭合，空泡溃灭等流动现象，并分析了落水流动机理及其水动力特性[8-9]。Mcgehee等[10]开展了返回舱原型和模型落水实验，定量分析了不同接触角和攻角落水的加速度峰值。何春涛等[11]、路中磊等[12]针对圆柱体低速入水空泡形态特性进行了实验研究，获得了不同速度下空泡闭合与演化规律。Grumstrup等[13]、Yang等[14]使用不同材料球体，开展了低弗劳德数条件下落水实验，解释了运动体落水过程的空泡波纹现象。Bodily等[15]通过在模型内嵌入内测单元，获得不对称亲疏水表面细长体落水加速度和角加速度的时变特性。Truscott等[16-17]、夏维学等[18]进行了大量的旋转小球落水实验，得到了旋转小球落水非对称的空泡演化现象，并分析了低弗劳德数旋转小球产生的水楔、马格努斯效应曲线轨迹等。Bocquet[19]、Rosellini等[20]采用实验和理论方法研究了刚性圆片落水弹跳现象，获得了不同弹跳周期内空泡演化、再落水抨击时间的变化规律，并建立了预测圆片运动和能量耗散的理论模型。Belden等[21]、Farouk等[22]分别通过实验和数值模型开展了小球落水弹跳研究，获得了小球落水多相流场演化，给出了基于高弗劳德数到低弗劳德数的渐进临界角的修正经验模型。

本文通过具有初始倾角的圆柱体在低弗劳德数条件下落水多自由度运动的数值分析，开展不同直径圆柱体大角度落水过程空泡演化规律研究，对比分析尺寸效应对落水空泡的影响，并获得圆柱体落水过程流体动力演化特性。

1 数值分析方法

本文针对圆柱体在低弗劳德数条件下落水过程，忽略流体介质的可压缩特性、空化和热效应，假设圆柱体为刚体。考虑到具有初始倾角的圆柱体落水过程的复杂性和非定常多相流动特性，采用基于VOF多相流模型的大涡模拟方法，以及重叠网格方法开展圆柱体落水过程复杂多自由度运动及流场演化特性研究。

1.1 基本控制方程

VOF多相流模型是适用于多种互不相溶的流体介质界面追踪技术，并忽略相间的相对滑移。对于仅涉及水和气两相的流动，定义αw为控制单元内水相的体积分数，其表达式为

αw=Vw/Vc

(1)

式中，Vw为控制单元内水介质的体积,Vc为控制单元的体积。根据以上定义， 1-αw为空气相体积分数，则给定控制单元内流体体积分数为：αw=1表示控制单元内全为水介质,αw=0表示控制单元内全为空气,0<αw<1表示控制单元由空气和水的混合介质组成。

控制单元内混合介质密度ρm和混合动力黏度μm表达式为

ρm=(1-αw)ρa+αwρw

(2)

μm=(1-αw)μa+αwμw

(3)

式中，ρa为空气相的密度，μa为空气相的运动黏度，ρw为水相的密度，μw为水相的运动黏度。

(4)

(5)

式中，xi为笛卡尔坐标，下标i=1,2,3分别代表笛卡尔坐标系x,y,z这3个坐标分量，下同；ui为笛卡尔坐标系下的速度分量；t为落水物理时间；p为控制体正压力；νm为混合运动黏度，定义为νm=μm/ρm；τij为亚格子尺度应力，针对不可压缩湍流流动的亚格子尺度应力张量模型为[24]

(6)

(7)

为了获得精确的近壁面湍流，本文数值分析采用WALE SGS模型[25]，则νt的定义为

(8)

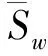
1.2 计算模型

本文基于Star-CCM+开展圆柱体落水过程多相流动特性研究。图1为圆柱体大角度落水的计算域及边界条件，该计算域与圆柱体落水试验的水箱一致[26]。计算域顶面的边界条件为压力入口，其余表面均为壁面边界，如图1所示。

图1 值模拟计算域和边界条件Fig.1 Computational domain and boundary condition

重叠网格技术被用于捕捉圆柱体落水后的复杂多自由度运动，图2给出了采用重叠网格技术的网格分布，其中圆柱体直径D=29 mm，长度L=180 mm。为了保障计算精度的同时提高计算效率，采用切割体网格法生成如图2所示的非结构背景网格。为了准确捕捉圆柱体落水后的水动力变化和空泡瞬态演化，在背景域中建立了10D×3D×12D和25D×3D×24D两个网格预加密区Ⅰ和Ⅱ。同时自由液面区域也进行了加密处理，以提高自由液面变化捕捉精度。为了更好地控制圆柱体壁面边界层网格的增长以及圆柱体域的网格分布，采用ICEM软件生成圆柱体域网格，如图2(c)所示,保证了在本文研究的圆柱体落水速度条件下满足y+<1的约束条件。采用直径为3D、长度为8D的圆柱计算域作为子计算域，数值分析过程将圆柱体表面边界条件设置为无滑移壁面，并给定固定接触角为67°。

为了研究尺寸效应对圆柱体落水多相流动的影响，以圆柱体直径D=29 mm为参考，在保证圆柱体落水速度v0= 2.5 m/s、倾角α0=120°、长细比、当量密度以及质量分布等初始参数相同的条件下，开展不同直径的圆柱体落水过程数值分析，表1中给出了圆柱体的详细参数。

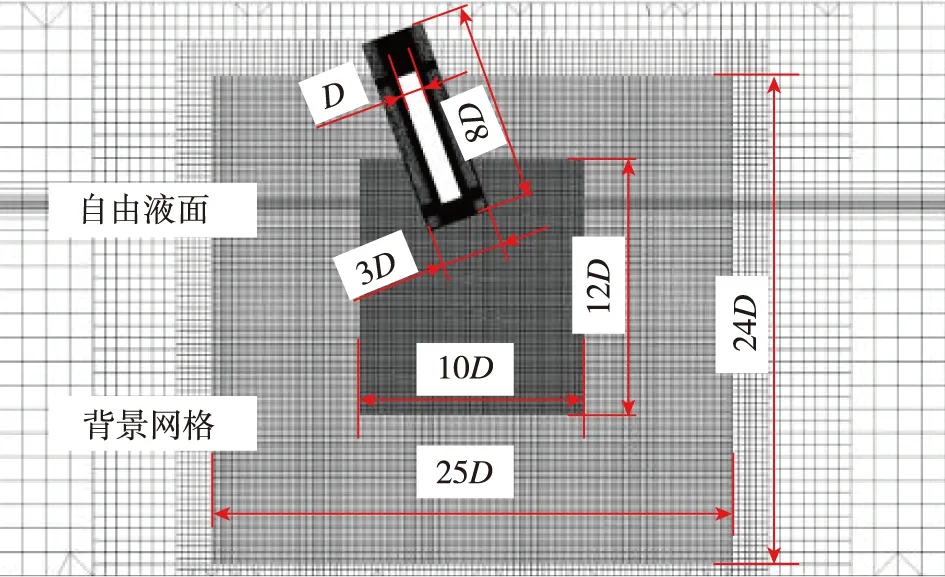
(a)xoy截面网格

(b)yoz截面网格

(c)圆柱体附近网格图2 计算域网格分布Fig.2 Distribution of the computational grid

表1 圆柱体参数

1.3 数值分析方法验证

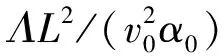
图3 圆柱体落水过程空泡演化实验和数值结果对比Fig.3 Comparison of the experimental and numerical cavity for cylinder entering water

图4 圆柱体落水加速度和角加速度变化时程数值和实验结果对比Fig.4 Comparison of cylinder acceleration and angular acceleration in water entry

2 结果分析

2.1 落水空泡演化过程

表2对比了不同直径圆柱体落水不同时刻的空泡形态，为了凸显直径变化对落水空泡的影响，通过定长高比缩放调节，保证图像中所有圆柱体直径相同。Truscott等[17,27]研究表明，运动体落水空泡闭合时间随其特征尺度的变化而变化。为了对比相对闭合时刻不同空泡形态，表2中图像提取时间间隔为0.2tp，同时给出了尾空泡闭合时刻tpt的图像。

对于直径D*≥0.75D的圆柱体，落水过程头空泡在空泡敞开、膨胀、分离、深闭合等演化过程高度一致，但是自由液面附近空泡口宽度(dcw)与圆柱体直径之比(dcw/D*)随直径增加而逐渐减小，而尾空泡的演化形式差异明显。首先，当水楔侵入尾空泡后，空气填充水楔尾部形成明显的尾空泡凸起现象，且圆柱体直径越小，凸起越明显(如表2中tp时刻)。其次，当D*=2D的圆柱体落水尾空泡直径较大，因此在当前落水速度下，沿圆柱体背流面的相对流动水射流没有切断尾空泡。图5(a)为圆柱体落水过程流场演化。图5(b)给出了表2中A-A截面空泡轮廓在tpt时刻的矢量分布。从图5中可以看到，尾空泡在水楔冲击作用下分裂为两个涡旋方向相反的空泡，最后对流旋转导致尾空泡闭合，而直径D*=1.5D,1D和0.75D的尾空泡均被沿圆柱体的水射流切断而形成闭合空泡。

不同直径圆柱体在落水相同时刻的速度高度一致，即直径越大的圆柱体壁面曲率越小，越不容易发生流动分离，反之亦然。因此，D*≥0.75D的圆柱体落水后均发生空泡从圆柱体表面分离的现象。然而对于直径D*=0.5D和0.25D的圆柱体落水空泡演化呈现明显的尺寸效应。圆柱体侧空泡形成后与头空泡连在一起形成连接空泡层。当圆柱体尾部浸没在自由液面下时，空泡层发生拉脱现象。随后，对于直径D*=0.5D的圆柱体，空泡层从拉脱位置自上而下破裂，直至空泡闭合溃灭。侧空泡在空泡层破裂后沿圆柱体壁面向尾部运动，空气不断逃逸至尾空泡中，导致尾空泡在闭合后仍形成较大的驻留空泡。

针对D*=0.25D的圆柱体，空泡层从头空泡闭合点附近自下而上破裂。空泡破裂后快速向尾部和向上流动，破裂射流携眷空泡冲击尾空泡使其闭合。空泡层在头空泡和尾空泡闭合后并未完全分裂(如表2中tpt时刻所示)。空气在空泡层快速收缩过程需通过连接头空泡的空泡层排出(如图5(c)所示为1.12tp时刻空泡内气体流动)，所以空泡层没有完全分裂。

(a)圆柱体落水过程流场演化

(b)A-A截面空泡轮廓速度矢量

(c)xoy平面空泡内速度矢量图5 局部速度矢量分布Fig.5 Local distribution of velocity vector

表2 不同直径圆柱体落水空泡对比

图6为无量纲头空泡闭合时间(v0tp/D)随弗劳德数Fr的变化。由表2空泡闭合形态可以看出，不同直径圆柱体落水头空泡均为拉断深闭合。即使是直径D*=0.25D的圆柱体，落水头空泡也是在环境压力作用下自中部附近向内收缩，然后出现空泡层破裂，并最终发生拉断闭合，即v0tp/D随Fr增加而线性增大。尾空泡的闭合形式比较复杂，很难仅根据尾空泡的演化结构去判断空泡是否闭合。

图6 空泡闭合时间随Fr的变化Fig.6 Change of pinch-off time as a function of froude number Fr

2.2 闭合特征尺寸

图7为不同直径圆柱体落水空泡闭合瞬间特征尺寸随Fr的变化。其中,图7(a)为头空泡闭合瞬间自由液面附近无量纲空泡口宽度dcw/D*随Fr的变化，图中横坐标以10为底的对数变化。从图7(a)中可以看出，dcw/D*随Fr的对数增加线性增长。头空泡闭合瞬间无量纲闭合点深度(hp/D*)以及圆柱体底面中心下降深(hb/D*)度随Fr0.5增加而呈线性增长，如图7(b)所示。同时，图7(b)中给出了hp/hb随Fr的变化，在本文研究范围内，hp/hb在Fr≤5.62时随Fr增加呈线性增长，而在Fr≥5.6范围内保持定值hp/hb≈0.48。

(a)空泡口宽度变化

(b)空泡闭合深度和圆柱体底面深度变化图7 不同直径圆柱体落水空泡闭合瞬间特征尺寸Fig.7 Cavity critical sizes at pinch-off moment for the cylinders with different diameters

(a)浸没深度

(b)水平偏移距离

(c)轨迹长度图8 空泡闭合瞬间圆柱体质心位置随Fr的变化Fig.8 Changes in cylinder center as a function of Froude number at pinch-off moment

2.3 水动力特性

本文采用瞬时动压力对圆柱体阻力、升力和力矩进行无量纲处理，得到圆柱体落水后的阻力系数Cd、升力系数Cl和力矩系数CM，其表达式为

(9)

式中，A= πD2/4为圆柱体横截面积。

2.3.1 升力系数

圆柱体落水升力系数Cl变化特性如图9所示。对于具有初始倾角的圆柱体撞击自由液面瞬间，底面下缘压强取得极大值[28]，如图9(a)所示。随后圆柱体侧壁面撞击水介质，Cl逐渐增大，直至头空泡发生闭合。空泡闭合瞬间在闭合点附近形成局部高压，由表2中tp时刻空泡形态可知，闭合压力导致圆柱体背流侧压力增加，使得压差力的方向与升力方向相反，所以Cl在空泡闭合时出现负向脉冲。空泡闭合后，圆柱体旋转诱导升力起支配作用且随圆柱体下降逐渐减小，但是圆柱体瞬时速度减小更快，因此Cl呈现缓慢增加的趋势。通过Cl随落水时间的变化发现，除去抨击和空泡闭合阶段外，Cl大致呈现线性变化，对空泡闭合前后的Cl进行线性拟合，获得如图9(b)所示的变化特性。

(a)升力系数随落水时间的变化

(b)空泡闭合前后升力系数渐进特性图9 不同直径圆柱体落水升力系数变化特性Fig.9 Properties of lift coefficients for the cylinders with different diameters

2.3.2 力矩系数

(a)力矩系数随落水时间的变化

(b)空泡闭合前后力矩系数渐进特性图10 不同直径圆柱体落水力矩系数变化特性Fig.10 Properties of lift coefficients for the cylinders with different diameters

2.3.3 阻力系数

图11(a)为不同直径圆柱体落水阻力系数Cd随落水无量纲时间t/tp的变化。圆柱体落水后Cd迅速增加，并在圆柱体底面中心没入自由液面后达到极大值。当落水速度一定时，到达极大值所需时间随D*增加而逐渐增加，且极大值随圆柱体直径增加也缓慢增加，如图11(a)中局部图ip所示。落水撞击阶段结束受后，Cd随圆柱体下降而逐渐增加。由图11(a)可见，不同直径圆柱体的Cd从撞击至头空泡闭合期间变化一致，但是在空泡闭合后出现明显分化，直径越小的圆柱体Cd在空泡闭合后增加越快。

空泡闭合前后Cd的平均增长率随Fr的变化如图11(b)所示。不同直径圆柱体落水的对数在空泡闭合前随Fr的对数增加而线性减小，分析发现随以自然数e为底Fr的指数变化的倒数1/eFr成线性关系。

通过上述分析可知，带倾角圆柱体垂直落水尾空泡闭合形式非常复杂，且很难仅根据尾空泡的演化形态定量测量尾空泡的闭合时间。但是，根据上述分析可知，尾空泡闭合形成的局部高压将导致圆柱体阻力减小，因此再结合Cd的变化，可以比较准确地判断尾空泡闭合时间tpt。

(a)阻力系数随落水时间的变化

(b)空泡闭合前阻力系数渐进特性图11 不同直径圆柱体落水力系数变化特性Fig.11 Properties of force coefficients for the cylinders with different diameters

从图11(a)中可以看到，不同直径圆柱体落水Cd在空泡闭合后存在两次较为明显的衰减，在图中分别用pt和ps表示。沿圆柱体表面的水射流切断尾空泡形成局部压力增加是导致D*=2D,1.5D,1D和0.75D的圆柱体阻力在pt时刻衰减的原因；而D*=0.25D和0.5D的圆柱体则是由头空泡闭合射流水楔冲击圆柱体壁面导致阻力衰减，因此从图中可以观察到Cd衰减明显(第一次衰减)。直径D*=2D,1.5D,1D和0.75D的圆柱体尾空泡被水射流切断后的上半尾空泡中间部分收缩、旋转最终发生拉断闭合，闭合形成的局部高压导致Cd出现明显的衰减现象；而D*=0.25D和0.5D的圆柱体落水，闭合射流不断抨击圆柱体壁面而释放了能量，所以Cd变化不明显，但是尾部空泡在闭合瞬间具有非常明显特征。因此，空泡形态和闭合水动力特征可以比较准确地判断尾空泡闭合。

图12为不同直径圆柱体落水空泡闭合后阻力系数第一次衰减及尾空泡闭合的无量纲时间随弗劳德数的平方Fr2的变化规律。第一次衰减的无量纲时间tptptv0/D的对数随Fr2的增加线性增长，如图12(a)所示。尾空泡无量纲闭合时间tptpsv0/D的对数随Fr2的对数呈线性增加，如图12(b)所示。

(a)第一次阻力系数衰减闭合时间

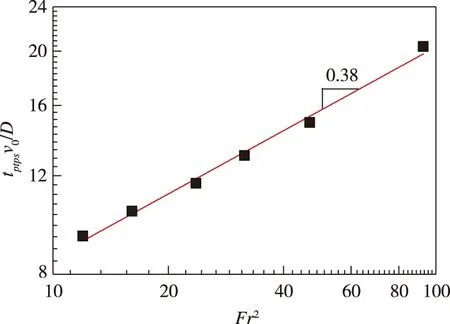
(b)尾空形闭合时间图12 不同直径圆柱体落水泡闭合后阶段特征时间随Fr2的变化Fig.12 The characteristic times after pinch off for water entry cylinders as a function of Fr2

3 结论

本文针对圆柱体大角度落水过程多自由度运动特性进行数值计算，对比分析了不同直径圆柱体落水空泡演化及水动力特性，主要结论如下：

1)数值分析获得的圆柱体落水空泡形态及受到的水动力与实验结果均高度一致，验证了本文所建立的数值分析方法的有效性。

2)直径大于临界值的圆柱体的落水头空泡敞开、膨胀、分离、深闭合等演化过程相同，但自由液面附近无量纲空泡口宽度随圆柱体直径增加而逐渐减小。直径小于临界值的圆柱体落水空泡演化呈现明显侧空泡现象。不同直径圆柱体落水头空泡均呈现深闭合，且空泡闭合无量纲时间随弗劳德数增加而线性增大。

3)除落水抨击和空泡闭合阶段外，空泡闭合前升力系数的平均增长率总体比空泡闭合后快。不同直径圆柱体的阻力系数从落水撞击至空泡闭合阶段变化一致，但是在空泡闭合后出现分化现象，直径越小的圆柱体阻力系数在空泡闭合后增加越快。