翼型空化起始对应空化数及尺度效应分析

常晟铭，丁恩宝，孙聪，王超，刘贵申

1 中国船舶科学研究中心，江苏 无锡 214082

2 哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001

0 引 言

空化是船海领域中经常发生的一种现象，因包含了相变、可压缩性、非定常等特点，长久以来一直是该领域的研究热点。一般而言，空化会带来一系列不利影响，空化起始和溃灭过程会使诸如鱼雷、艇体、螺旋桨等海洋结构物发生剧烈振动，进而引发噪声、结构破坏、效率降低等问题，所以也是海洋结构物需要极力避免的现象[1]。虽然空化对海洋结构物的危害一直是研究者们关注的问题，但对于其成因仍无定论。目前，广为接受的表述是由Franc 和Michel 提出的，即空化是液体介质在过高应力作用下的碎裂过程，高温和低压的条件均会使液体介质的水分子间的拉应力剧烈增加，使液体发生碎裂并发生空化。在一定温度下的临界压力便被称为饱和蒸汽压[2]。此外，空化的发生还离不开一种削弱其抗拉强度的物质，这种物质被称为“汽核”[3]。

近年来，许多研究者针对空化，特别是与翼型空化相关的机理问题进行了研究。例如，刘志辉[4]采用OpenFOAM 开源软件，数值模拟二维水翼的非定常云空化，分析云空化形成过程及其分级断裂现象，验证了一种非线性湍流模型及其适用性。结果表明，该非线性湍流模型在研究梢涡空泡的过程中具有一定优势。剧冬梅等[5]采用实验方法对Clark-Y 翼型的空化特性进行了研究，通过改变不同攻角，观察空化数对翼型空化形式的影响机理，结果表明，随着空化数的不断减小，空化可以划分为初始空化、片空化、云空化和超空泡这几个类型。其中，云空化对翼型的水动力特性影响程度最大，亦即显著增加了翼型的阻力，减小了翼型的升力，从而带来一系列不利影响。丁恩宝等[6]采用STAR-CCM+软件，分析不同尺度下翼型在流场域中的压力场，以及通过改变流速确定翼型空化起始点对应的临界雷诺数，分析尺度效应，结果表明，尺度较大的翼型其临界雷诺数也较大。

从目前来看，虽然研究者采用了许多方法研究了翼型空化问题，但对于翼型空化尺度效应的研究却十分片面，仅是从临界雷诺数下产生尺度效应的角度进行了研究，而未引入空化模型。因此，关于空化起始点的尺度效应问题还需要更深入的探究。

本文将以标准KCS 船使用的NACA 0012 翼型船舵作为参照，使用SSTk-ω 湍流模型和基于输运方程的S-S 空化模型，通过改变环境压强来改变空化数，寻找空化起始对应的临界空化数，然后对比不同缩比尺翼型空化起始点的流场、压力场、表面压力分布，研究不同攻角下翼型空化起始对应的临界空化数随尺度变化的尺度效应，并分析相应的机理。

1 数值计算方法

1.1 湍流模型

本文使用的模型为SSTk-ω 湍流模型[7-8]，其中k，ω 的输运方程分别为：

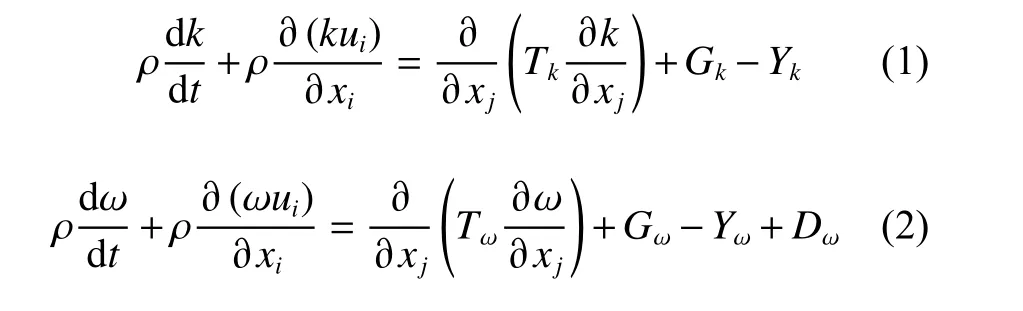
式中：Gk为由层流速度梯度产生的湍流动能；Gω为由ω 方程产生的湍流动能；k和ω 分别为湍流动能及耗散率； ρ为流体密度；ui为速度分量的时均值；xi和xj为位移分量；Tk和Tω分别为k和ω 的扩散率；Yk和Yω为由扩散产生的湍流；Dω为正交发散项。

1.2 空化模型

在研究空化问题时，普遍采用的是均质混合流模型，主要思想是将空化发生时的液体和蒸汽两相视为由球形汽泡及液体两种成分组成的混合流，能够将多相连续介质简化成一个包含汽核的单相连续介质，进而通过控制方程求解。而Schnerr-Sauer 空化模型（以下称S-S 空化模型）是一种基于均质混合流的输运方程模型[9]，其中汽相体积分数的定义为

构建S-S 空化模型源项的表达式为

2 计算模型

2.1 流场域划分和工况设置

图1 所示为划分的计算域。其中，左侧边界为速度进口，右侧边界为压力出口，上、下边界为对称平面。为满足黏性流体力学条件，翼型表面的工况被设置为不可滑移壁面。计算域左侧速度进口的边界距离翼型左缘2 倍弦长（C），右侧压力出口的边界距离翼型的右缘6 倍弦长，上、下两个边界距离翼型上缘和下缘均为2 倍弦长。流体密度和动力黏度系数为25 ℃的液态水参数，设置流体密度为997.561 kg/m3，动力黏度系数为8.887 1×10−4Pa·s。

图1 计算域的划分Fig. 1 Division of computational domain

本文参照标准KCS 船所使用的NACA 0012型船舵，翼型的初始尺度与船舵的弦长一致，为5.5 m，而流场的流速对应KCS 船的航速24 kn，即12.345 m/s。分别采用1:3，1:10 和1:20 缩尺比翼型进行尺度效应的研究。在研究尺度效应时，因参照了实船舵所选取的翼型，一般需要保证弗劳德数相等，而若要保证弗劳德数相等，不同尺度之间的翼型所对应的流场流速会有一定差异，导致雷诺数的不同，并带来尺度效应。表1 给出了不同尺度翼型对应的弦长及流场流速。

根据前人的研究经验，平板湍流的边界层厚度需与其对应的雷诺数及参照长度相关，具体的数量关系为[10]

式中：h为平板湍流边界层厚度；L为参照长度，本文即翼型的弦长；Re为对应的雷诺数。

因缩尺比的变化会导致表1 所示的翼型雷诺数发生变化，根据式（9），所以对应的边界层厚度也会产生较大差异，进而对网格划分带来一定影响，即影响到近壁第1 层棱柱层厚度和棱柱层厚度。经公式推导，不同缩尺比翼型对应的棱柱层厚度及近壁面第1 层棱柱层厚度如表2 所示。

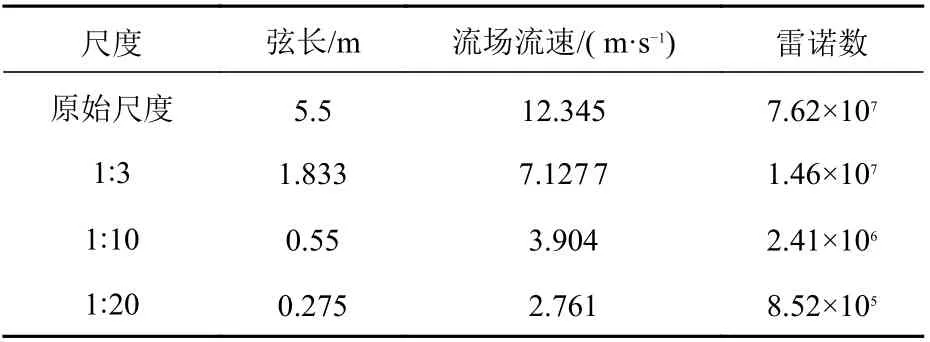
表1 不同尺度翼型的工况设置Table 1 Working condition setting of different scale models of hydrofoil

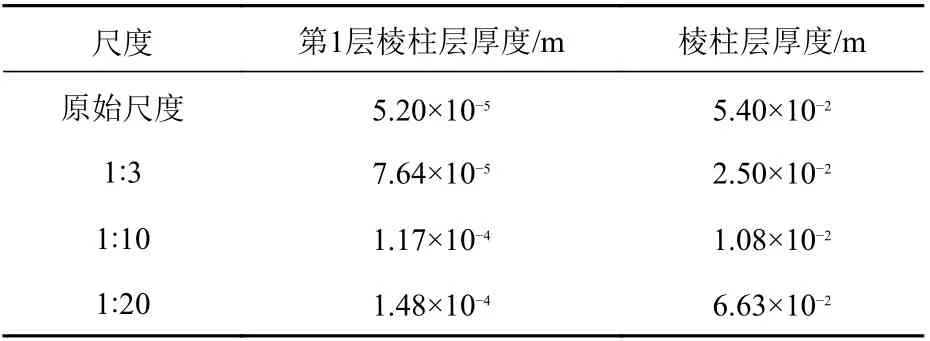
表2 不同尺度翼型的边界层参数设置Table 2 Boundary layer parameter setting of different scale models of hydrofoils

本文需要对不同缩尺比和攻角的翼型空化起始所对应的空化数进行研究。对应的空化数定义如下：

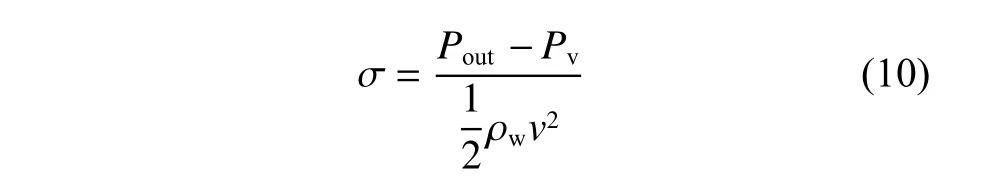
式中： σ为空化数；Pout为出口压力，即环境压强；ρw为液体密度；v为进口速度。

2.2 网格划分

本文采用的网格为切割体网格和棱柱层网格相结合的形式，其中，翼型表面的边界层设置为棱柱层网格形式，流场域网格设置为切割体网格形式。为提高计算精度，将翼型上表面前缘位置的网格和尾流区进行了一定程度的加密。最终，确定了如图2 所示的网格划分形式。当改变翼型缩尺比时，需通过改变对应网格基础尺寸的方式，将整个计算域作放大或缩小处理。

图2 网格划分Fig. 2 Mesh division of computational domain

为验证网格的收敛性，本文按照图2 所示的网格划分形式，通过改变网格的基础尺寸，选择了3 套不同加密形式的网格进行收敛性验证。模型计算工况如下：弦长为5.5 m、原始尺度翼型攻角为5°、空化数为1.15。具体网格数及3 套网格划分模型所对应的升力系数CL和阻力系数CD如表3 所示。

表3 网格收敛性分析Table 3 Mesh convergence analysis

由表3 可见，相较于较为粗糙的Mesh-1 网格加密形式，Mesh-2 和Mesh-3 这两种加密形式的网格模型二者的升力系数和阻力系数的值较接近，因此网格加密到Mesh-2 的程度已可以满足对计算所需精度的要求，无需进一步细化网格。此外，本文还需对空化起始的机理作一定的研究，网格收敛性验证中需对比翼型表面压力分布。具体结果如图3 所示。

由图3 可见，3 种不同网格加密形式的翼型表面压力分布结果之间差异并不显著。因此，基于上述网格收敛性分析结果，本文最终确定了Mesh-2 网格加密形式。

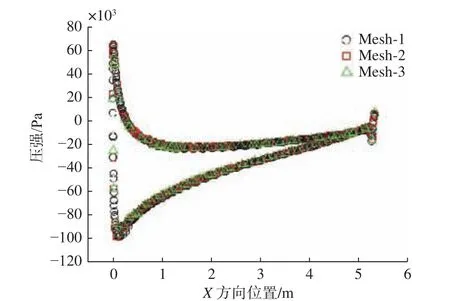
图3 不同网格加密形式的翼型表面压力分布对比Fig. 3 Comparison of surface pressure distribution of hydrofoil with different forms of mesh refinement

2.3 模拟值与试验值对比

为证明本文所用方法的合理性，将Mesh-2 网格加密形式应用于攻角6°、弦长0.15 m 的NACA 66翼型，以及在雷诺数Re=8×105工况下通过数值模拟方式得到的升阻比(CL/CD)与试验值[11]进行对比，如图4（a）所示。图4（b）给出的是空化数为1.41 时的空泡分布结果。

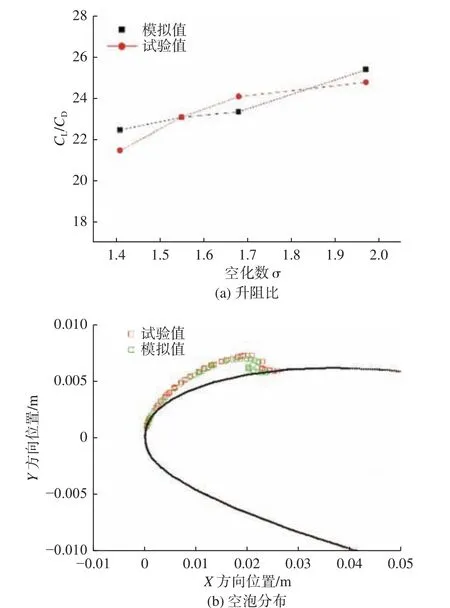
图4 模拟值与试验值的对比Fig. 4 Comparison between simulations and experimental results

由图4 可见，在现有Mesh-2 网格划分的基础上，数值模拟结果与试验值较接近，也就是说，数值模拟能够精确模拟出翼型周围的流场，并可解决与翼型空化起始相关的水动力机理问题。

3 计算结果

3.1 空化起始对应空化数的确定方法

为确定空化起始对应的临界空化数，应明确空化形式随着空泡数的不断减小，会逐渐发展为起始空泡、片空泡、云空泡、超空泡这几种形式。根据式（10）的定义，当环境压强足够大时，空泡数会很大，空化并不会发生。因此，在保证翼型周围流速一定的情况下，设置足够大的环境压强，然后再不断减小环境压强，直至空化数缩小到起始空化发生之时，即可确定对应工况下空化起始对应的临界空化数。图5 所示为原始尺度翼型（弦长5.5 m 的NACA 0012 翼型）0°攻角时的空化起始对应空化数的确定方式。

图5 翼型空化起始对应空化数的确定方式Fig. 5 Method for ascertaining the cavitation number corresponding to cavitation initiation of original scale hyrofoil

根据前人的经验[4]，将汽相体积分数分布的最大值设置为0.1 时能够清晰地捕捉到空化边界，故本文也遵循此设置方法。由图5（a）所示空化数为0.45 时的汽相分布结果不难看出，此时因环境压强较大，液体难以发生汽化，空化并不会发生。而当空化数减小至0.40 时（图5（b）），因环境压强过低，空化已发展为片空化形式，并非空化起始形式。最终，通过在0.40～0.45 的空化数范围内改变环境压强，可以得到如图5(c)所示的空化起始形式，最终确定空化起始对应的临界空化数为0.43。

3.2 空化起始对应空化数随攻角的变化

在流场流速保持一定时，若改变翼型的攻角，周围的流场特性也会随之发生一定的改变，并影响翼型空化起始对应的空化数。本文以原始尺度翼型为例，给出了攻角与空化起始对应空化数之间的关系，如图6 所示。

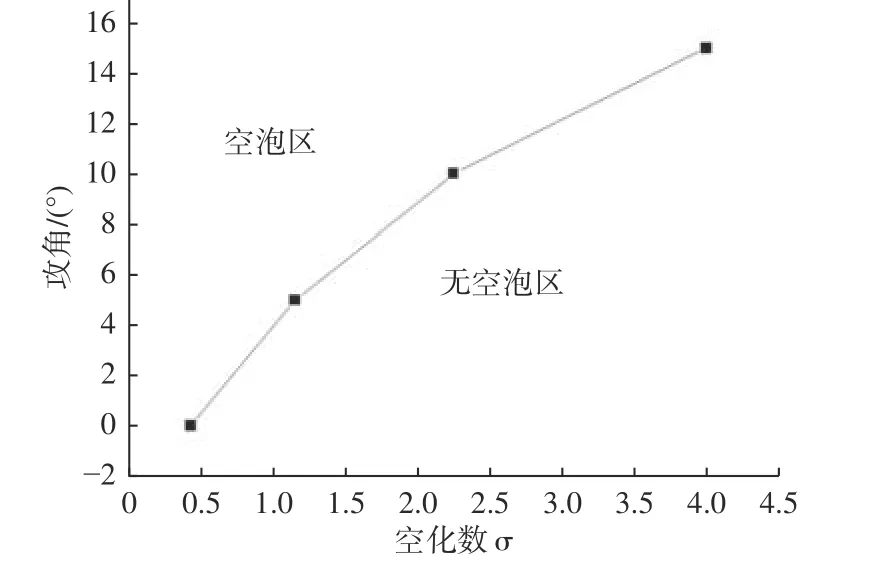
图6 原始尺度翼型空化起始对应空化数与攻角的关系Fig. 6 Relationship between cavitation number and attack angle corresponding to cavitation initiation of original scale hydrofoil

由图6 可见，原始尺度翼型的空化起始对应的临界空化数随攻角的增加而不断增大，二者的关系呈现为斗状曲线，一般被称为“空泡斗”[12]。在空泡斗的内部，因空化数大于空化起始对应的临界空化数，空化难以发生，所以此区域也被称作“无空泡区”；而空泡斗的外部因空化数会小于空化起始对应的临界空化数，在翼型上表面强吸力峰的位置形成空化，所以空泡斗的外部区域也被称作“空泡区”。

图7 所示为原始尺度翼型在不同攻角时对应的空化起始点空泡形态分布图。

由图7 可见，随着攻角的不断增加，翼型空化起始位置逐渐向翼型前缘方向移动。在攻角为0°时，翼型上、下两个表面均有空化起始，但在有攻角之后，空化起始的位置接近于翼型上表面前缘位置。从空化起始的发展程度来看，翼型攻角较小，即0°和5°时，空化起始的发展程度较小，但随着翼型攻角的不断增大，例如10°时，翼型附近流场发生了较大变化，从而影响到翼型上表面低压区域的面积，因此空化起始的发展程度也会有所增强。为深入分析流场对空化起始点的作用机理，提取了5°和15°攻角下翼型周围的流线图（图8）、速度矢量图（图9）和压力云图（图10）。

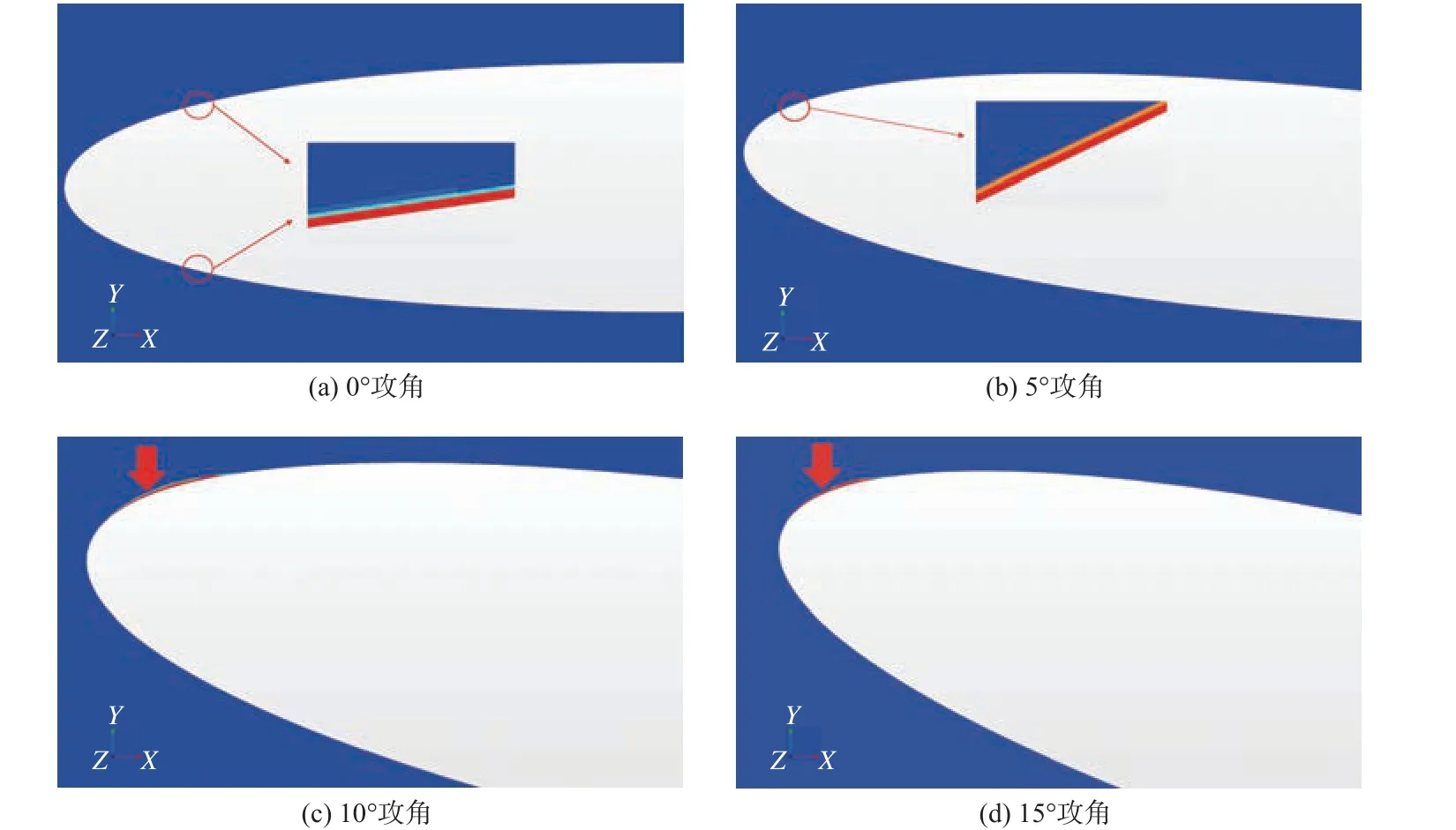
图7 原始尺度翼型空泡起始点空泡形态分布随攻角的变化Fig. 7 Variation of the cavitation shape distribution of the cavitation initial point of the original scale hydrofoil with attack angle

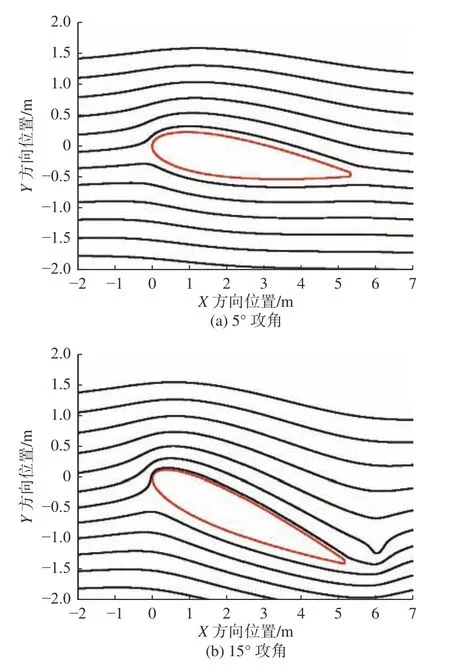
图8 不同攻角翼型周围的流线分布Fig. 8 Streamline distribution of hydrofoil at different attack angles

由图8 可见，翼型周围的绕流场整体上比较平稳，但其前缘及尾缘附近的流线有一定程度的扭曲。相较于5°攻角时的情况，15°攻角时的翼型前缘流线扭曲程度更高，分布密度也更大，使得前缘附近流场的流速更大，流速较大的区域也明显增加，如图9 所示。

图9 不同攻角翼型的速度矢量分布Fig. 9 Velocity vector distribution of hydrofoil at different attack angles

根据伯努利原理（Bernoulli's theorem），在同一流线上流速越大的位置压力越小。因此，一方面，翼型前缘附近流场的流速较大会导致压强有所降低，更容易低于水的饱和蒸汽压，即空化更容易起始于翼型前缘位置的附近；另一方面，在15°攻角时，翼型前缘附近较大流速所在的区域较大（图9），使得翼型前缘附近的低压区域面积较大（图10），从而极大地增加了此时翼型空化起始的发展程度。

图10 不同攻角翼型的压力云图Fig. 10 Pressure contours of hydrofoil at different attack angles

根据科恩达效应（Coanda effect），翼型前缘附近的流体会贴近翼型轮廓流动，受到一个向心力的作用，其大小朝向翼型方向，来源于流场中流体压力的合力。这证明了翼型前缘附近的流场压力较小，容易发生空化的这一结论。

3.3 空化起始对应空化数的尺度效应

随着翼型尺度的变化，翼型雷诺数也会有一定的变化，进而发生尺度效应，使得空化起始对应空化数有所变化。为探究此时翼型的尺度效应，本文选择了1:3，1:10，1:20 缩尺比翼型进行分析，得到了不同攻角翼型时空化起始对应的空化数，如图11 所示。

由图11 可见，1:3 缩尺比翼型并未受到尺度效应的影响，说明无论攻角如何变化，翼型空化起始对应的空化数均与原始尺度翼型的相同。但是，随着翼型缩尺比的变小，翼型空化起始对应的空化数也均有所降低，且翼型缩尺比越小，空化数降幅越大。相较于其他攻角的情况，15°攻角翼型空化起始对应的空化数与原始尺度翼型的差别非常大，说明此时的尺度效应最明显。图12 给出了15°攻角翼型空化起始对应的空化数随缩尺比的变化趋势。

图11 不同尺度翼型空化起始对应空泡数与攻角的关系Fig. 11 Relationship between cavitation number and attack angle corresponding to cavitation initiation of different scale hydrofoils

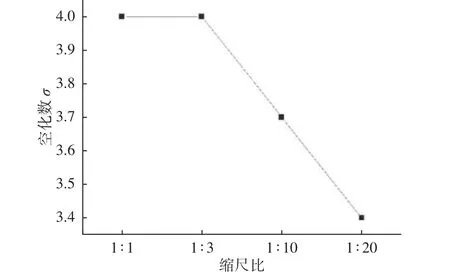
图12 15°攻角翼型空化起始所对应空泡数的尺度效应Fig. 12 Scale effect of cavitation initiation corresponding to cavitation number at fifteen degrees attack angle

对于翼型空化起始所对应的空化数，改变翼型缩尺比，其受到的尺度效应影响随之变化，空化起始位置也随翼型缩尺比的变化而变化。图13给出了5°，10°，15°不同攻角翼型的空化起始位置受尺度效应的影响情况。

由图13 可见，各攻角下，随着翼型缩尺比发生变化，翼型空化起始位置也都因尺度效应而改变。具体而言，在翼型缩尺比缩小的情况下，翼型空化起始位置逐渐向其后缘方向偏移，而空化起始的发展程度也随之逐渐增强。因此，在研究水翼时，特别是模型试验研究中，翼型尺度效应的影响不容忽视，采用的水翼模型尺度也不可与实体尺度相差过大。

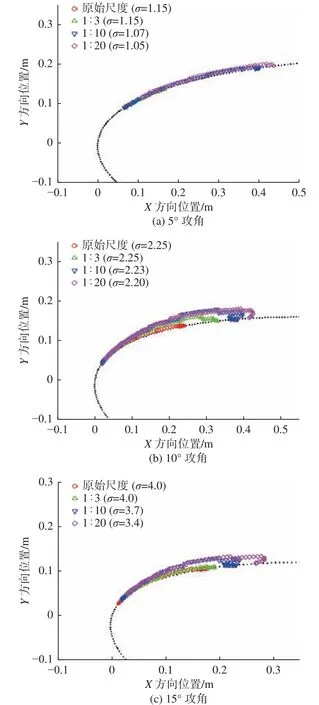
图13 不同攻角翼型空化起始位置随尺度的变化Fig. 13 Variation of cavitation initiation position of hydrofoils with scale at different attack angles

为探究尺度效应对翼型空化起始对应的空化数及其位置的影响机理，本文提取了15°攻角下原始尺度翼型和1:20 缩尺比翼型的流线图、速度矢量图和压力云图进行对比，分别如图14、图15和图16 所示。

由图14 可见，对于原始尺度和1:20 缩尺比翼型，在15°攻角下二者的空化起始位置、流线密集程度和形状扭曲程度几乎相同，未受到尺度效应的影响。但是，在尺度效应的影响下，1:20 缩尺比翼型上表面的第1 条流线与翼型之间的间距明显大于原始尺度翼型。相同的结果同样在图15 所示的速度矢量分布中得到反映，即原始尺度翼型周围流体流动与翼型上表面的贴合程度大于1:20缩尺比翼型的情况。

造成上述现象的原因是，采用式（9）计算边界层厚度后，1:20 缩尺比翼型边界层的相对厚度要大于原始尺度翼型的边界层厚度。二者边界层厚度之间的差异，一方面使得1:20 缩尺比翼型附近流场受到黏性的影响较大，特别是贴近翼型表面的流体分子受到较大的黏性剪应力作用，阻碍了流体流动；另一方面，会影响到控制方程的求解及边界层的转捩过程，以及不同缩尺比翼型周围流场的分布，通过伯努利原理使翼型周围压力分布产生如图16 所示的差异，带来了一系列的尺度效应，最终影响了空化起始对应的空化数及其位置和形态。

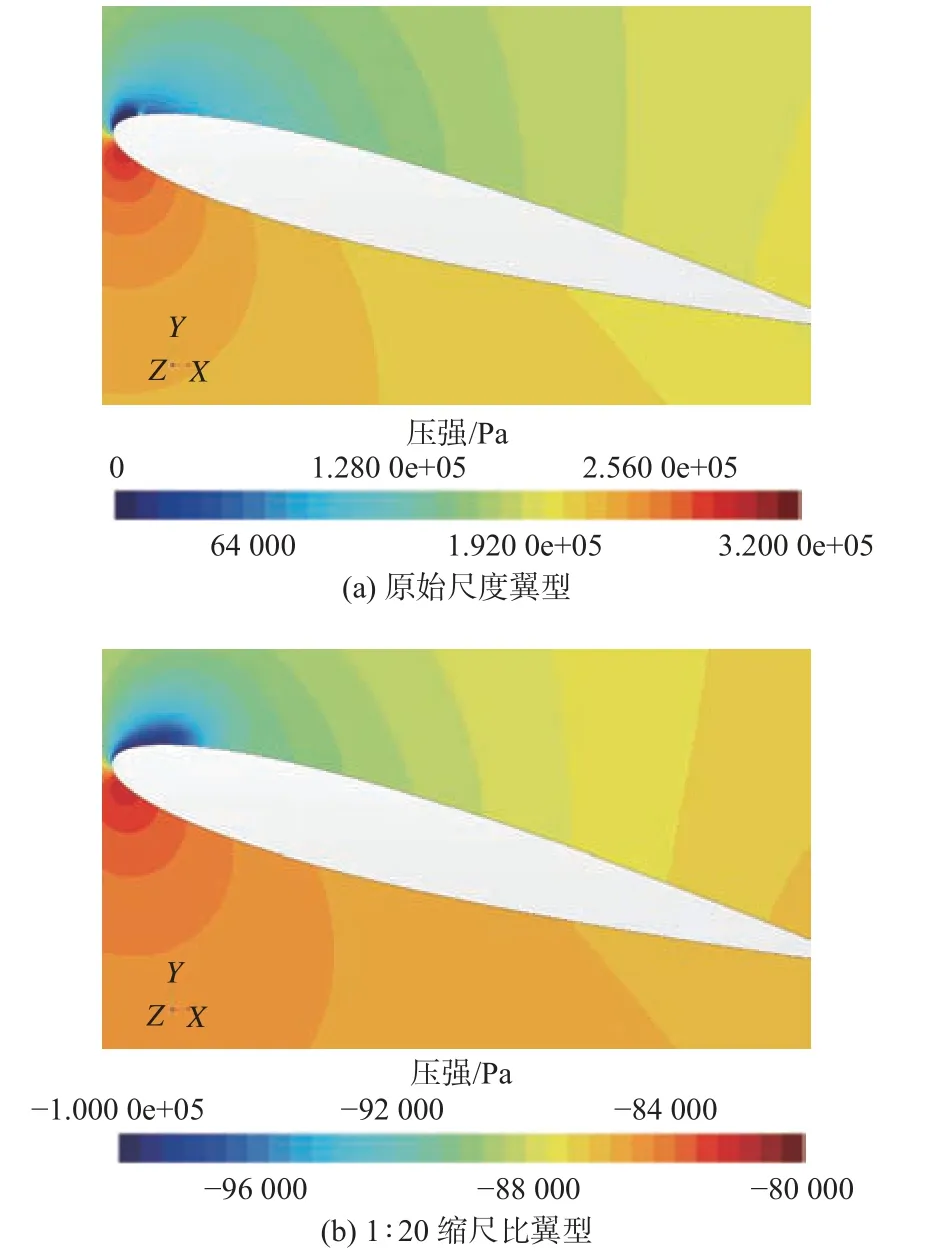
图16 不同尺度翼型15°攻角下的压力云图Fig. 16 Pressure contours of different scale hydrofoils at fifteen degrees attack angle

4 结 论

本文采用了STAR-CCM+软件，采用SSTk-ω湍流模型和S-S 空化模型数值模拟了翼型空泡特性，分析了不同缩尺比翼型的空化起始对应空化数受尺度效应的影响，得到了如下的结论：

1） 对于相同缩尺比翼型，随着攻角的增大，空化起始对应空化数有所增大，二者的关系呈现为一个斗状曲线，也称“空泡斗”。

2） 随着翼型攻角的增大，翼型空化起始位置不断向翼型前缘的方向移动，空化起始的发展程度随之增强。其原因在于，随着翼型攻角的增大，翼型前缘流线的扭曲程度有所增强，分布密集程度也更大，前缘附近流场流速也有所增大。根据伯努利原理和科恩达效应，流场的差异作用于压力场，使得翼型空化起始受到影响。

3） 随着翼型尺度的缩小，不同缩尺比翼型空化起始对应的空化数均有所降低，尺度越小，翼型空化起始对应空化数降低的幅度越大，即受尺度效应的影响越大。而翼型空化起始位置随尺度的减小向翼型后缘方向偏移，发展程度随尺度的减小而有所增强。造成尺度效应的原因是，翼型周围边界层的相对厚度因不同雷诺数带来的差异而有所变化，影响了翼型表面流场受到的黏性剪应力作用，以及控制方程的求解和边界层转捩的过程。

针对翼型空化的尺度效应问题，未来还需要进一步开展如下研究：

1） 本文所述翼型空化研究仅限于二维层面，而空化往往是一个三维及非定常的问题，特别是对于三维尺度的翼型空化问题，在三维翼型端部还会形成一个内卷的流向涡，发生梢涡空化。上述三维特性通过二维方法是无法研究的，未来应在三维基础上研究翼型空化问题。

2） 对于翼型空化的尺度效应研究，空化起始的尺度效应仅是其中一小部分。空化按照其发展阶段包括了起始空化、片空化、云空化和超空化，这些阶段发生点对应的空化数及空化形态均因雷诺数的差异会带来一系列尺度效应，这也是未来需要着重研究的方面。