海洋内波影响水下航行体水动力特性数值模拟

汪超，杜伟，李广华，杜鹏*，赵森，李卓越，陈效鹏，胡海豹

1 西北工业大学 航海学院，陕西 西安 710072

2 武汉第二船舶设计研究所，湖北 武汉 430205

3 郑州机电工程研究所，河南 郑州 450015

0 引 言

地球表面四分之三的海洋长年受到太阳热辐射的作用，海水的温度、盐度和密度在铅直方向上形成了稳定的层化结构，当外力扰动破坏了这种分层结构时，就可能产生内波[1]。海洋表面的大气压力、风场、地震以及水下航行体的运动等均可成为引发内波的扰动源。内孤立波是一种特殊的非线性内波，其非线性和频散相平衡，通常以单个波包或波包列的形式出现，最显著的特征是可以维持一定的波形、波速长距离传播，距离可达上百公里。此外，内孤立波还携带有巨大能量，在海洋内部产生大幅垂向波动的同时，会导致密度跃层上下的海水流动呈现剪切状态，引起海水强烈的幅聚幅散和突发性的强流[2]。

内孤立波在我国附近海域十分活跃，南海东南部吕宋海峡至大陆近海均为内孤立波高发海域[3]。水下航行体遭遇内孤立波时，其运动稳定性、悬停姿态和水动力特性都有可能会发生突变或失控，导致水下航行体运动失稳、操纵失控等[4]。海洋内孤立波已成为水下航行体安全航行中必须考虑的一个灾害性环境因素，迫切需要针对内孤立波与水下航行体的强非线性作用问题开展研究工作，分析内孤立波作用下航行体的水动力特性，并给出内孤立波载荷的作用规律。

实验研究是客观认识内孤立波与水下结构物相互作用的重要途径，但由于受到内波水槽尺度、分层流体制备以及测量技术的限制，数值模拟逐渐成为国内外学者研究内孤立波与水下结构物耦合作用问题的重要方法，并且开展了大量的相应研究。陈杰等[5]以两层流体中内孤立波的KdV-mKdV 理论解为基础，模拟了内孤立波与运动潜体之间的相互作用，得到了带速潜体所受的荷载特性，为以后研究内波与运动潜体的相互作用开辟了一条新路径；关晖等[6]应用双推板造波法模拟内孤立波数值水槽，采用有限体积自适应半结构多重网格法研究了上凸、下凹两种内孤立波的载荷效应，并分析了水下航行体在海洋中遭遇内孤立波时的流场形态和受力特性。Gou 等[7]通过时域数值模型计算了水平淹没圆柱遇到界面孤立波时的垂直运动，结果表明下凹内孤立波接近潜体时，自身的垂直力和位移变化较大。黄苗苗等[8]基于RANS 方法和KdV 理论建立了分层流中的内孤立波与水下航行体相互作用的数值模拟方法，发现内孤立波会使得航行体周围流场变得异常复杂，从而引起突变的流体动力和运动，需对此时的航行安全性应给予极大重视。Zou 等[9]对海洋内孤立波与水下浮洞（SFT）之间的相互作用进行了数值研究，分析了内孤立波振幅、SFT与密跃层的相对距离、SFT 截面几何形状以及两流体层密度比对水平力、垂向力系数的影响。Liu等[10]研究了分层流中潜艇的阻力和尾迹，结果表明潜艇的下潜深度显著影响其水动力性能，当其接近内界面时，会产生更大的阻力。

当前国内外相关研究大多针对某一工况下内孤立波与海洋结构物相互作用的载荷特性开展，对于不同内波环境对海洋结构物水动力特性的影响仍缺乏进一步研究。鉴于此，本文拟通过CFD仿真软件Fluent 模拟分层流中内孤立波与固定、悬浮航行体的相互作用，对不同内波环境下航行体的水动力特性变化进行深入研究，以得到波体耦合的作用规律和影响机理。

1 数学模型

1.1 内孤立波理论

实际海洋密度呈现多层不均匀分布，为简化求解，通常将海水假设为两层、均匀分布的流体，忽略密跃层厚度，将分界面看作密度跃层。设上层流体的深度和密度分别为h1和 ρ1，下层流体的深度和密度分别为h2和 ρ2，假设流体无旋且不可压缩。考虑到上、下层流体密度差异不大，内孤立波在传播过程中自由面诱导的垂向速度基本可以忽略，故流体域顶部采用了刚盖假设，底部设为刚性不可渗透的固壁。建立直角坐标系xoz，振幅为a的内孤立波沿ox轴向右传播，以竖直向上为z轴正方向，水平向右为x轴正方向，如图1 所示。

图1 两层流体之间的内孤立波Fig. 1 Internal solitary wave between two layers of fluid

设内孤立波为永形波，以波速c沿ox轴正方向传播，Ui(i=1,2)表示第i层流体质点的平均速度，对波面位移ζ(x,t)做如下变换：

则两层Green-Naghdi 模型可化为如式(2)所示的KdV 方程。

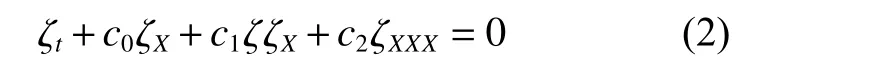
式中：c0，c1和c2分别为线性项系数、非线性项系数和色散项系数。KdV 理论要求非线性和色散之间是平衡的，是描述两层流体下内孤立波最早的理论模型。其在方程中保留了非线性项，对于大振幅内孤立波来说，非线性与色散性之间不一定平衡。现有的实验研究表明，内孤立波振幅较小，即a/h<0.1时（其中h表示总水深），采用KdV 方程进行数值模拟与实验吻合良好，而当a/h>0.1时，数值结果误差较大。这主要是由于内孤立波的KdV 理论模型不存在理论极限振幅，因而其不适用于大振幅的内孤立波。

为了弥补KdV 理论只能适用于小波幅内孤立波的缺陷，在式(2)中引入一个立方非线性项，得到eKdV 方程：

eKdV 方程适用于波幅不超过极限波幅的内孤立波。而mKdV 方程[11-12]适用于波幅从0 到h¯变化的情况（h¯是界面与临界水平hc之间的距离）。其界面位移ζ(x,t)的解为上式中：cm为波的相速度； λm为特征波长；g为重力加速度。

mKdV 方程模拟内孤立波垂向分布的水平速度最接近实验结果，适用于各种上、下层厚度比，具有较强的非线性[13]。因本文模拟的尺度接近实验室尺度，且数值造波方法是利用水平速度入口造波，故采用mKdV 方程作为造波理论的基础。

1.2 数值方法

计算模型采用美国国防高级研究计划局（DARPA）的SUBOFF 潜艇标准模型，缩尺比为1:10。缩小后艇体总长为0.435 m，最大回转直径为0.051 m，附体包括指挥台和垂直艉翼，艉翼剖面为NACA 0020 翼型，对称布置于艇艉部，潜体重心水平位置距离艏部0.203 m。为了提高计算效率，悬浮、自由运动航行体与内孤立波耦合模拟中选择光体SUBOFF 模型，详细参数见表1。

表1 SUBOFF 模型几何参数（缩尺比1:10）Table 1 Geometric parameters of SUBOFF model (Scale 1:10)

数值水槽长H=15 m，总水深h=1 m，设上层流体的深度和密度分别为h1=0.2 m和ρ1=995 kg/m3，下层流体的深度和密度分别为h2=0.8 m 和ρ2=1 023 kg/m3，流体动力黏度为µ=0.001 N·s/m2，重力加速度g=9.81 m/s2。SUBOFF 模型放置在工作区，其艏部距离入口边界7 m，计算域的后5 m为消波区，计算域示意图如图2 所示。

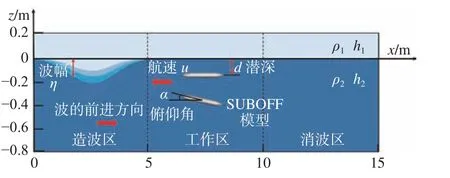
图2 计算域示意图Fig. 2 Schematic diagram of the computational domain

重叠网格方法不涉及网格变形及重构，在模拟瞬时大幅运动方面比传统的变形网格方法更有优势，而且更容易调整航行体的初始位置，因此，本文采用重叠网格方法模拟内孤立波与潜艇的相互作用。对数值水槽和潜艇模型分别进行结构化网格划分，在潜艇表面处使用渐变网格，使嵌套网格和背景网格能够均匀过渡，边界层网格划分保证y+<1（如图3 所示）。消波区网格逐渐粗化，以增强数值耗散。边界条件设置如下：水槽左侧为速度入口，右侧为压力出口，上表面为Symmetry边界，底部边界为无滑移壁面。

图3 重叠网格示意图Fig. 3 Schematic diagram of the overset grid

通过mKdV 理论方程计算得到内孤立波在传播过程中诱导的上、下层流体平均水平速度U1和，将速度控制方程通过UDF 加载到入口边界上进行数值造波。

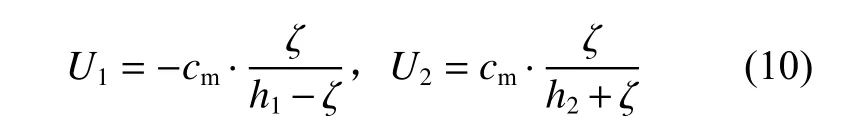
流场通过求解不可压黏性流动纳维−斯托克斯（N-S）方程组得到，其控制方程为：

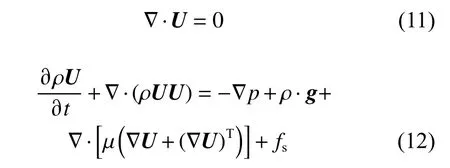
式中：U为流场速度； µ为动力黏性系数； ρ为流体密度；p为流场压强；fs为添加到消波海绵层中的源项。

航行体多自由度运动控制方程为：

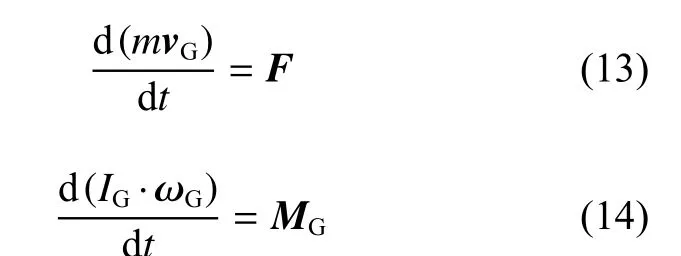
式中：m为 航行体的质量；vG，F，IG， ωG以及MG分别为航行体的速度矢量、所受合外力、转动惯量、转动角速度和所受惯性矩，下标G 表示重心。

通过求解不可压缩、有黏N-S 方程得到流场中航行体的受力和力矩，再将其代入多自由度运动方程中，求解获得航行体的加速度与角加速度，积分得到航行体各角速度与速度分量，代入控制方程后进行下一时间步网格更新与数值计算。如此反复迭代，直至达到设定的收敛精度或给定时间。在计算过程中，流体作用在航行体上的力和力矩使航行体运动，同时航行体壁面也对流场产生影响。

初始时水槽中流场速度均取为零。在入口处施加速度入口边界条件，采用压力出口方法处理定常来流出流问题，同时采用海绵层方法对内孤立波进行数值消波。内孤立波形成于两层流体之间的分界面处，采用流体体积 (volume of fluid,VOF)方法来捕捉两相界面的变化。数值处理求解器为非定常隐式求解器，控制方程采用有限体积法（finite volume method, FVM）进行离散，对流项以及湍流输运项采用二阶迎风格式离散，时间离散方式采用一阶隐式，压力速度耦合设置为PISO，节点压力梯度计算采用最小二乘法，动量方程为二阶迎风格式，时间步长取0.005 s。

1.3 算例验证

为验证后续数值结果的准确性，对照黄文昊等[15]的实验工作设置圆柱型结构内孤立波载荷模拟算例。数值水池大小为30 m×1 m×1 m (长×宽×高)，水池中竖直放置一直径D=0.15 m的圆柱，吃水深度l=0.535 m，距离入口LS=7 m，如图4 所示。上下层流体深度、密度、黏度系数以及数值设置同1.2 节。

图4 验证算例示意图Fig. 4 Schematic diagram of the verification example

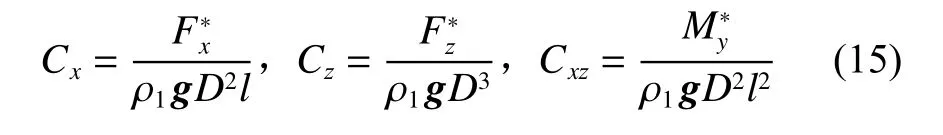
处理后的结果与文献[15]试验结果的对比如图5 所示。由图5 可知，分层水槽中竖直圆柱上内孤立波载荷特性与试验结果基本吻合，表明利用该数值方法来模拟分层流中内孤立波与水下航行体相互作用是合理可行的。

图5 模拟结果与试验结果对比Fig. 5 Comparison of simulations with experimental results

1.4 算例设置

下文将探究不同内波环境对水下固定、悬浮航行体水动力特性的影响，在模拟中改变波幅、潜深、航速和俯仰角。研究波幅对航行体水动力特性的影响时，分别设置波幅η为0.1、0.15 和0.2 m，航行体在流体分界面下方0.1 m 处保持水平状态，即潜深d=0.1 m、俯仰角α=0◦和航速u=0 m/s；研究潜深对航行体水动力特性的影响时，设置航行体的潜深d分别为分界面以下0.02、0.06 和0.12 m，保持波幅η=0.1 m、俯仰角α=0◦和航速u=0 m/s；对于固定航行体，增加了俯仰角对其水动力特性影响的算例，分别设置航行体初始俯仰角 α为0°、6°和10°，保持波幅η=0.1 m、潜深d=0.1 m和航速u=0 m/s；而对于悬浮航行体，研究航速对其水动力特性的影响时，在不同时间段内分别给定航行体的运动状态。0～20 s 是造波阶段，航行体处于固定状态，保持波幅η=0.1 m、潜深d=0.1 m和初始俯仰角α=0◦，工况设置示意如图2 所示；20～30 s航行体加速至0.5 m/s；30 s 后，在航行体将要遇到内孤立波时开启航行体的纵向、垂向和俯仰运动3 个自由度。

为简化下文数据分析，这里对各物理量进行无因次变换。

式中：Fx，Fz和My分别为内孤立波作用下航行体所受到的水平力、垂向力和力矩，力矩转动中心为航行体重心，水平力向右为正方向，垂向力向上为正方向，力矩逆时针为正方向； ρ¯为上下层流体平均密度；A为 航行体最大横截面积；t为计算时间。

2 内孤立波与固定航行体

2.1 波幅的影响

由图6(a)可知，航行体所受水平力的趋势基本一致，均为先向右增大，后向左增大，但随着内孤立波波幅的增加，航行体所受水平力的最大值不断增加，航行体受力曲线开始变化的时间也随之提前，受力周期也不断变短。其原因在于，当增大内孤立波波幅时，航行体具有的能量增加，波速也会随之增加，但特征波长会随之减小；那么，大波幅内孤立波会更快接触到航行体，在更短时间内通过航行体。由图6(b)可以看出：航行体所受垂向力的趋势也基本一致，均为先向下增大后向上增大，随着内孤立波波幅的增加，航行体所受垂向力的最大值不断增加，航行体受力曲线开始变化的时间也随之提前，且所受垂向力的受力周期也不断变短，其原因与水平力曲线变化的原因一致；波幅越大，垂向受力波动越明显。由图6(c)可以看出，航行体所受力矩的整体趋势基本一致，均为先顺时针增大，后逆时针增大，但随着内孤立波波幅的增加，航行体所受力矩的变化曲线振荡更加明显，受力开始时间也随之提前，且力矩的受力周期也不断变短。

图6 不同波幅内孤立波作用下固定航行体水动力载荷数值结果Fig. 6 Numerical results of hydrodynamic loads on fixed vehicle under the action of internal solitary waves with different wave amplitudes

2.2 潜深的影响

由图7(a)航行体所受水平力变化曲线可以看出，航行体位于流体分界面下0.02 和0.06 m，即d′=0.02和0.06时，其所受水平力的变化趋势类似，但位于流体分界面下0.12 m（d′=0.12）时，航行体受力在幅值和相位上存在差异，且初始先受到向左的水平力。这主要是因为潜深0.02 和0.06 m的固定航行体穿过内孤立波，内孤立波向右运动使航行体先受到向右的水平作用力，而潜深为0.12 m的航行体没有直接与内孤立波作用，受到的是内孤立波诱导的流场，下层流体质点运动方向均为向左，所以航行体先受到向左的作用力；潜深为0.02 m 的航行体受到的水平力幅值最大。由图7(b)垂向力的变化曲线可以看出，航行体在不同潜深处所受到的垂向力的变化趋势相同，航行体穿越内孤立波时所受到的垂向力大于未穿过内孤立波情况下的垂向力，d′=0.02时航行体所受垂向力的幅值和作用时间均大于d′=0.06时的航行体。由图7(c)力矩的变化曲线可以看出，航行体在穿越内孤立波和位于波谷下方时，航行体所受到的力矩的变化方向先顺时针增大，后逆时针增大。在航行体穿越内孤立波波面的工况下，内孤立波靠近航行体导致流场中出现涡结构，在波面右侧流场中存在向下的垂向速度，对航行体艏部产生向下的作用力，从而出现一个小幅度逆时针的力矩，之后航行体穿越内孤立波右波面。然而，由于波面是向下凹的形状，航行体穿越波面时，其艇体艏部上方应当先接触到上层流体，因而其艏部上方受到的压力变小，航行体艏部下方的压力大于上方压力，航行体受到顺时针的力矩，并且随着内波向右运动，其所受到的力矩不断增大；当航行体重心通过波面后，航行体艉部下表面受到的压力大于其上表面的压力，航行体艉部受到向上的作用力，因而顺时针力矩会出现小幅度的减少；当航行体穿出内孤立波左波面时，其艏部下方先接触到下层流体，且受到的压力变大，而大于艏部上方的压力，仍然受到顺时针的力矩作用。之后，内孤立波逐渐远离航行体，但在波面左侧，由于涡结构的存在，流场中存在向上的速度，航行体艉部受到向上的作用力，出现逆时针的力矩。且随着航行体深度的增加，力矩幅值波动逐渐减小，力矩曲线也更加平滑，说明航行体潜深越接近两层流体分界面，其力矩变化情况越复杂，存在更多的不确定性，对航行体的航行安全会产生严重影响。

图7 不同潜深处固定航行体的水动力载荷数值结果Fig. 7 Numerical results of hydrodynamic loads on fixed vehicle at different depths

2.3 俯仰角的影响

由图8(a)可以看出，不同俯仰角下航行体受到内孤立波作用产生的水平力的变化趋势与周期基本一致，但随着俯仰角的增加，航行体所受水平力的最大值不断增加。其原因在于，航行体俯仰角增加后，其水平迎流面积也随之变大，受到流速及流速方向不同而导致的摩擦力也会随之增大；而在水平方向上航行体的受力仅由内孤立波的流动引起，所以水平力的最大值随着俯仰角增加而不断增大。同时，从水平力的曲线变化还可以看出，当俯仰角不断增大时，水平力曲线振荡程度也随之增强，俯仰角越大，曲线越不平滑，一方面说明二维情况下航行体对流体的阻塞对于流场影响较大，使内孤立波波形不稳定，并在一定程度上也体现出带有俯仰角的航行体受力情况更加复杂，对航行体航行安全影响更大。由图8(b)可以看出，航行体受到内孤立波作用产生的垂向力的变化趋势与周期也几乎相同，但随着俯仰角的增加，航行体所受到的负方向垂向力的最大值不断减小，而正方向的最大值基本保持不变。由图8(c) 可以看出，随着航行体俯仰角的增加，航行体所受力矩的趋势更加明显，并且负方向力矩的最大值也随之增大，而正方向力矩则随之有一定的减小。

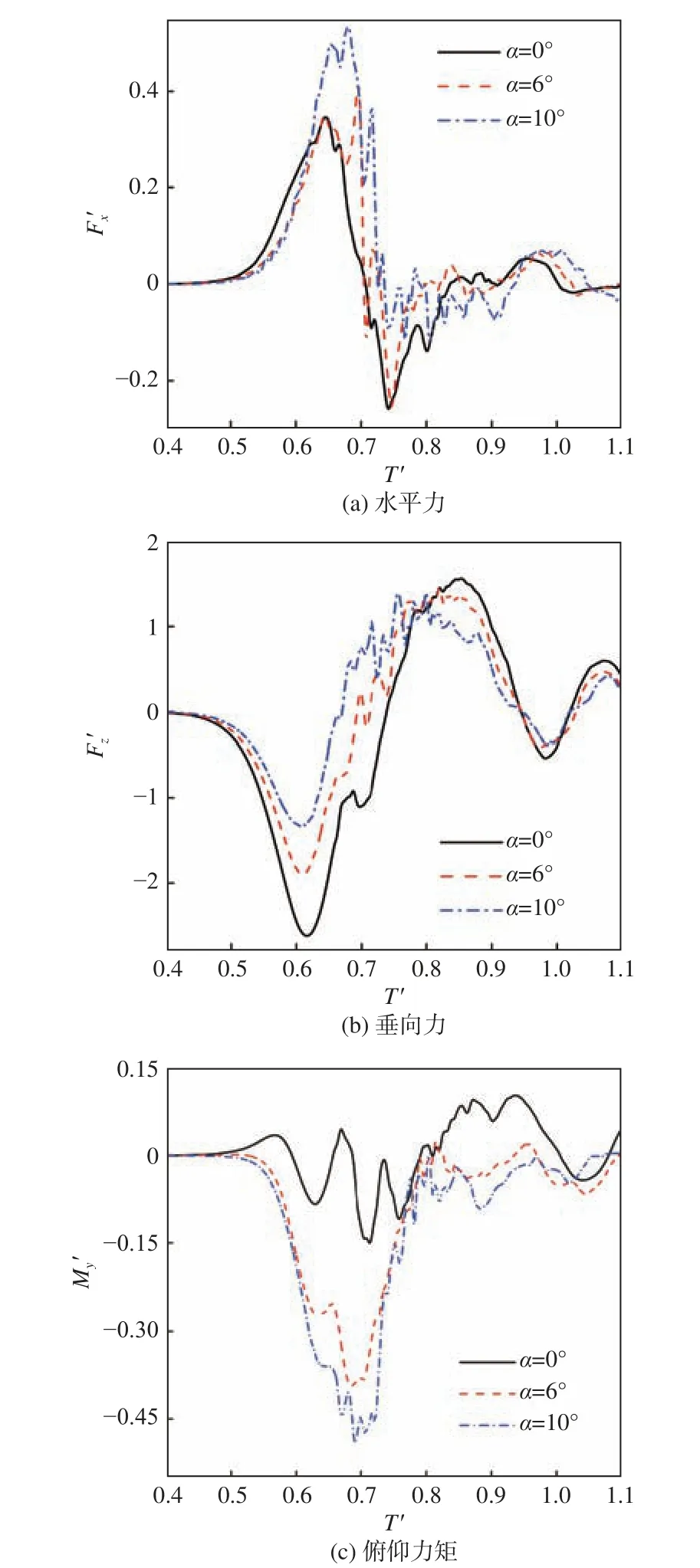
图8 不同俯仰角姿态下固定航行体的水动力载荷数值结果Fig. 8 Numerical results of hydrodynamic load on fixed vehicle under different pitch angles

3 内孤立波与悬浮航行体

3.1 波幅的影响

图9 所示为不同波幅内孤立波作用下悬浮航行体水动力载荷数值结果。由图9(a)可以看出，不同波幅内孤立波作用下航行体所受水平作用力的变化趋势基本相同。由于航行体都是位于分界面下0.1 m 处，在内孤立波诱导的顺时针流场作用下，悬浮航行体先受到向左的水平力，这个水平力较小。在航行体逐渐接近内孤立波波谷位置，向左的作用力逐渐减小，到达波谷所在的中垂线附近时，此时水平力为0，此后，航行体背离内孤立波，受到的水平力向右并逐渐减小；且波幅越大，航行体受到的水平力幅值越大。由图9(b)可知：航行体在内孤立波流场的作用下，其初始状态就受到一个向下的力，压着航行体朝下方加速运动；当内孤立波越过航行体后，垂向力变成向上，航行体继续朝下方做减速运动；波幅越大，航行体受到的垂向力也越大。由图9(c)可知：航行体的俯仰力矩与垂向力的关系比较大，η′=0.15和η′=0.20结果曲线变化相近，且力矩的幅值要略大于η′=0.10的算例，力矩曲线振荡较大；航行体先低头再快速抬头，内孤立波过去之后又开始低头。

图9 不同波幅内孤立波作用下悬浮航行体水动力载荷数值结果Fig. 9 Numerical results of hydrodynamic loads on suspended vehicle under the action of internal solitary waves with different wave amplitudes

3.2 潜深的影响

从图10 整体水动力载荷数值结果来看，悬浮航行体所受的水平力、垂向力和俯仰力矩变化趋势一致，仅载荷幅值略有差异。由图10(a)可知：在下层流体中的航行体受到的水平力先向左，后向右，这是由于涡的速度方向是顺时针的；当航行体接近内孤立波波谷时，此时水平力向左逐渐增大，过了波谷之后水平力朝右增大。从图10(b)可以看出：航行体在竖直方向先受到向下不断波动的垂向力，当航行体到达内孤立波波谷位置时，垂向力变为0；随着内孤立波继续向右行进，越过航行体后短暂时间内垂向力朝上，但是在惯性力作用下，航行体还是低头朝下运动。从图10(c)可以发现：航行体初始位于下层流体，其艏部受到流场的作用力低头向下，因此初始力矩为低头力矩；随着波的向前推进，航行体尾部流体向下的速度不断增加，航行体受到抬头力矩；内孤立波波谷经过航行体，流体想要把航行体往上推，由于二维的阻塞作用，只能使航行体逆时针低头。

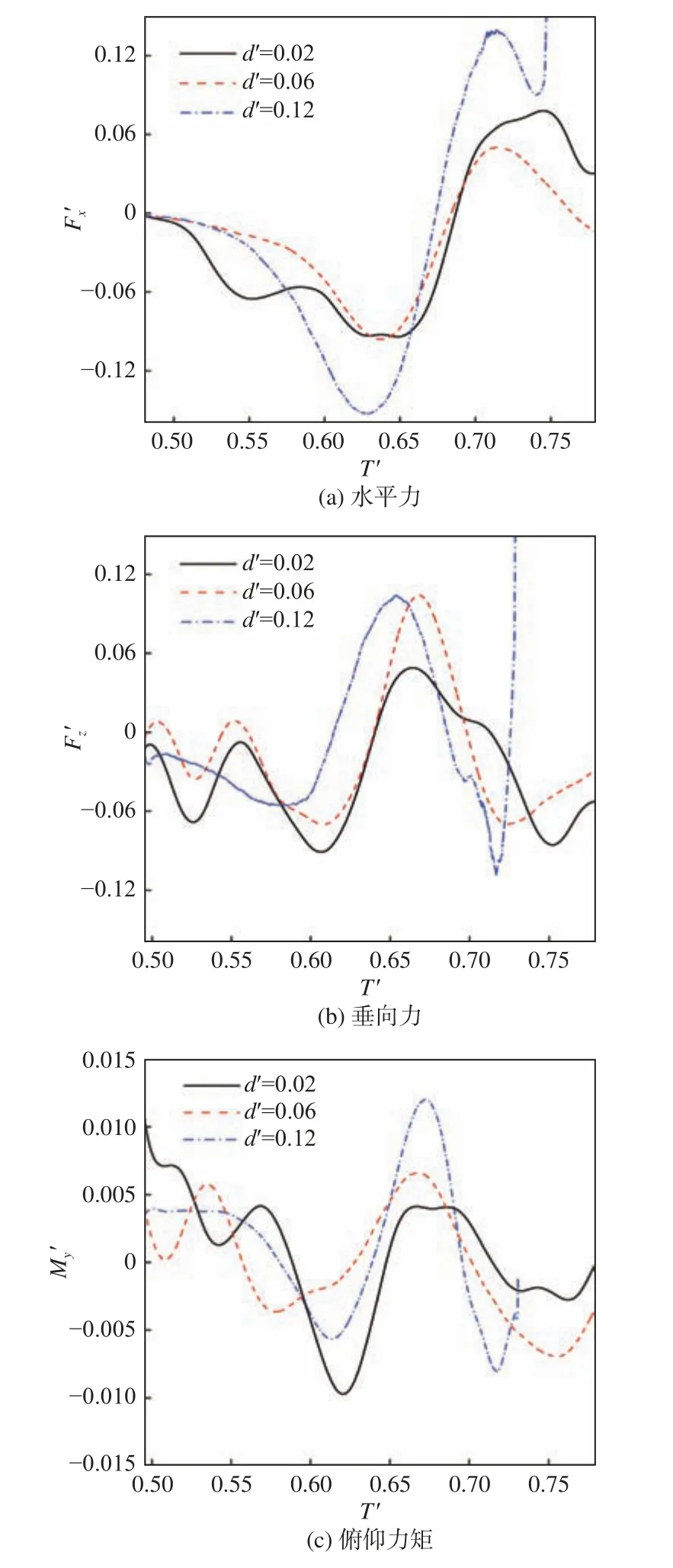
图10 不同潜深处悬浮航行体的水动力载荷数值结果Fig. 10 Numerical results of hydrodynamic loads on suspended vehicle at different depths

3.3 航速的影响

由之前的结果可以发现，位于分界面下层的航行体遭遇内孤立波会产生剧烈的晃动并导致“掉深”现象的发生，本案例就是具有初始航速的航行体，本节分析其在内孤立波作用下的受力和运动情况，并讨论潜艇发生剧烈晃动和“掉深”的原因。

图11 所示为运动航行体与内孤立波相互作用过程的变化情况。由图中可以看出，航行体经过内孤立波波谷中垂线之前，其俯仰角度基本没有变化，而在经过波谷中垂线后开始低头向下运动。

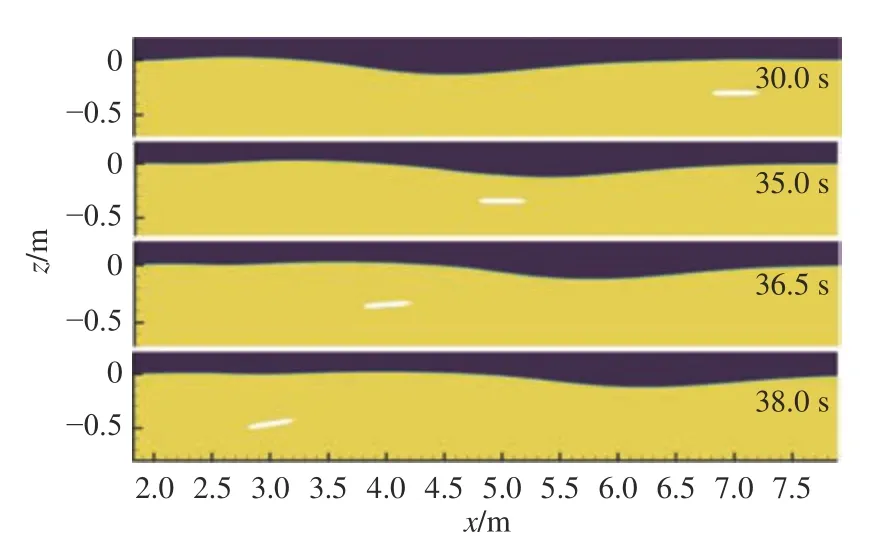
图11 运动航行体与内孤立波的作用Fig. 11 Interaction between moving vehicle and internal solitary wave

动压表示流体颗粒每单位体积的动能，也可以理解为驱动流体流动所需要的压力。图12 所示为36.5 s 时刻动压场Dp中航行体附近的流线图。从动压场来看，航行体艏部上下动压相差不大，但航行体艉部上下动压相差较大；将航行体附近的流场放大并绘制流线，可以清楚地看到，内孤立波经过航行体之后，其逆时针转动的流场会作用到航行体的艉部，航行体受到一个逆时针旋转的力矩，有低头的趋势；此外，内孤立波行进过程中，常伴随着尾波的产生，尾波会消耗主波一部分能量，且与主波流场旋向相反，此时航行体刚好处于主波和尾波之间，若继续向左运动，其艏部会受到内孤立波尾涡的“拍击”作用，航行体不能维持自身平衡，进而会发生“掉深”现象。

图12 36.5 s 时刻动压场中航行体附近流线图Fig. 12 Streamline near the vehicle in the dynamic pressure field at the moment of 36.5 s

4 结 论

本文主要研究了不同内波环境对航行体水动力特性的影响规律。主要结论如下：

1） 对于固定航行体而言，内孤立波波幅越大，航行体所受水平力、垂向力和力矩的峰值越大，航行体受载曲线开始变化的时间也随之提前，并且受力周期也不断变短；内孤立波波幅越大，航行体受载的变化曲线振荡越明显。航行体潜深越接近两层流体分界面时，其所受水平力和垂向力峰值越大、力矩变化情况变得更加复杂，存在更多的不确定性，对航行体的安全会产生严重威胁。随着航行体俯仰角的增大，其所受水平力、力矩峰值也随之增加，相反地，垂向力随着俯仰角的增加而减小。

2） 对于悬浮航行体而言，内孤立波波幅越大，航行体上的水平力、垂向力峰值也越大，力矩曲线变化振荡更大。潜深越接近于内孤立波波谷纵深位置，悬浮航行体的水动力载荷峰值越大，受影响的时间越长。

3） 具有初始航速的航行体穿过内孤立波后，会发生“掉深”现象，其原因可能是由于航行体艉部受到内孤立波主波流场向上的作用力，艏部受到尾涡的“拍击”，导致航行体失去平衡进而发生“掉深”。