促深度理解 助主动建构——《平行四边形的面积》教学设计(二)

文|徐 妍

【教学内容】

苏教版五年级上册第7、8页。

【教学过程】

一、情境导入，唤醒经验

师：乐乐喜欢做手工，用细木条钉成一个长方形框，仔细观察，你能提出哪些数学问题？

生：这个长方形的周长是多少？

生：长方形的面积是多少？

师：同学们很善于思考，我们一般在研究平面图形时，经常会研究到它的周长和面积。长方形的周长和面积会求吗？

生：周长=（长+宽）×2，面积=长×宽。

师：假期里，同桌毛毛对这个框很感兴趣，将长方形改造成了平行四边形，仔细观察，你有办法求出改造后的平行四边形面积吗？

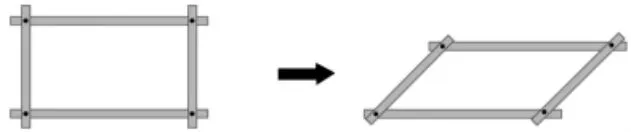
【设计意图：通过情境导入，唤醒学生对长方形这类平面图形的旧知，在实际情境中回忆长方形的周长和面积计算，唤醒经验的同时，为后面的对比发现、探索比较埋下伏笔。】

二、自主探索，经历过程

1.激发猜想，引发冲突。

师：这节课我们来研究平行四边形的面积。

研究一：下面这个平行四边形的面积是多少平方厘米呢？（量出你需要的数据，取整厘米数，标在图上，并列式算一算）

师：老师挑选了三位同学的作品，一起来看。

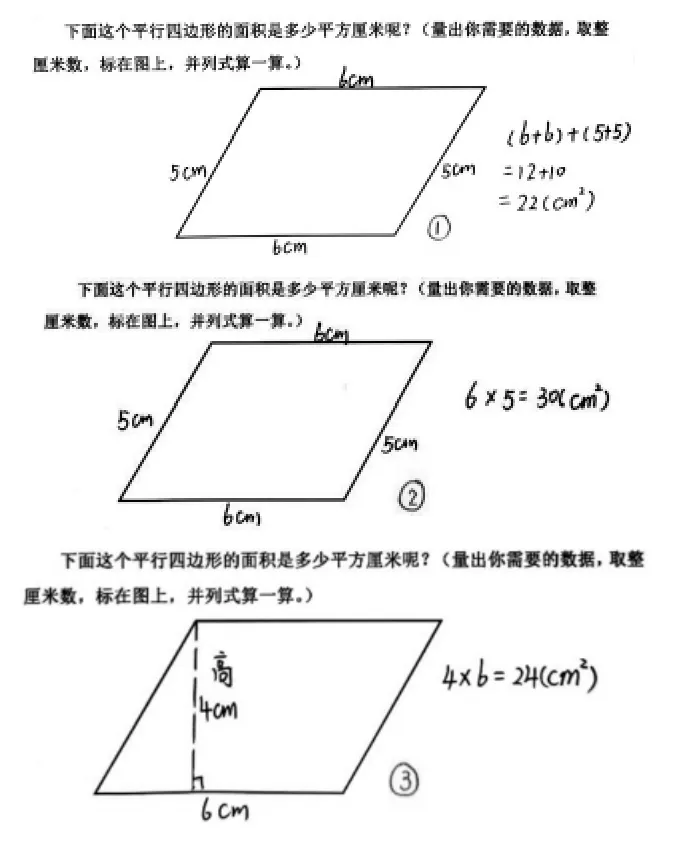
师：仔细观察，你有什么想说的？

生1：我觉得①号肯定不对，这是在求周长。

生2：我觉得②号正确，我感觉就是用6乘5，像长方形求面积一样，长方形求面积就是这样算的。

生3：我不同意②号正确，你看那个平行四边形被压扁了，面积比原来的长方形面积小，不可能是30平方厘米，我觉得应该是③号。

生4：我也觉得③号是正确的，我知道平行四边形的面积就是底×高。

师：同学们充分表达了自己的观点，现在你们认为哪一种答案是正确的？

（大部分同意③号，个别坚持②号）

师：有争论特别棒，接下来，用你们喜欢的方法来说明你们的结论是正确的。

2.经历过程，操作验证。

（学生动手尝试研究）

师：怎么说明这个平行四边形的面积是多少呢？

生1：我是用转化的方法，分成三部分，旋转平移一部分后变成一个长方形进行面积计算。

生2：数方格的方法，我是一个一个数，先数整格的，不满一格的当作半格来数。

师：同学们用喜欢的方法说明了这个平行四边形的面积是24平方厘米。

师：现在你觉得该怎样计算平行四边形的面积？

生：平行四边形的面积=底×高。

师：刚才我们通过一个具体的例子研究，感觉平行四边形的面积和它的底、高有关。是不是所有的平行四边形的面积都可以用“底×高”来计算呢？

【设计意图：放手让学生充分展示自己的想法，暴露思维的原生态，大胆地猜想，激烈地讨论，从而激起学生的探究欲，有利于进一步进行探索。】

3.深入研究，得出结论。

研究二：每人一个平行四边形，同桌合作（同桌两人的平行四边形相同），借助你手上的平行四边形，能推导出平行四边形的面积=底×高吗？（事先准备大小、形状不同的平行四边形，每组同桌的相同）

师：活动前，先想一想你准备怎样研究呢？

生：剪一剪、拼一拼。

（学生在操作过程中剪、拼其中一人的平行四边形，另一个平行四边形不动，进行对比）

（学生画一条高，用剪刀剪下这条高，原来的平行四边形变成两部分，拼成长方形）

（沿着平行四边形的高剪，再进行拼，转化为长方形，平行四边形的底就是长方形的长，高就是长方形的宽。因为长方形面积等于长乘宽，所以，平行四边形面积等于底乘高）

师：如果用S表示平行四边形的面积，用a表示平行四边形的底，用h表示平行四边形的高，平行四边形面积的计算公式是——

生：S=a×h。

师：回顾刚才的过程，用割、补、平移的方法把平行四边形转化成了长方形，用旧知识解决了新问题，推导出了平行四边形的面积公式，真了不起。

【设计意图：是不是所有的平行四边形面积都可以用“底乘高”来进行计算呢？从“一个”触发，准备走向“一类”。学生通过已有的感觉与经验觉得似乎是可以的，随着教师出示不同大小、不同形状的平行四边形，有很扁的那种，有竖着摆的，通过不同的“变式”图形让学生观察并思考。在对不同平行四边形面积推导的过程中，学生进一步验证了之前的猜想。】

三、分层练习，巩固新知

1.快速口算：计算下面各平行四边形的面积。

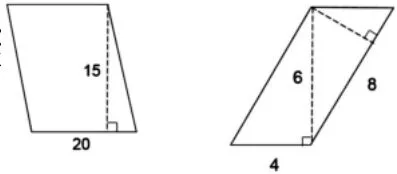
2.一个平行四边形，相邻两条边的长分别是12厘米和8厘米，高是10厘米，面积是（ ）。

师：和同桌说说你的想法。

（学生上台现场画图进行解释说明）

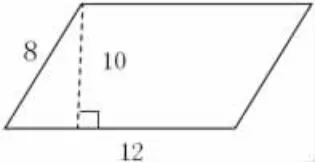
（斜边比高要长）

【设计意图：练习是课堂教学中必不可少的环节，是学生理解运用、完成整体建构的过程，在这里，重点突出平行四边形的底和高的对应关系，让学生画图解释，不断丰富学生的空间观念。】

四、对比延伸，完整建构

师：我们再次回到刚上课的画面，还记得用细木条钉成一个长方形框，变成了平行四边形吗？如果将平行四边形拉、拼成长方形又有什么变化呢？

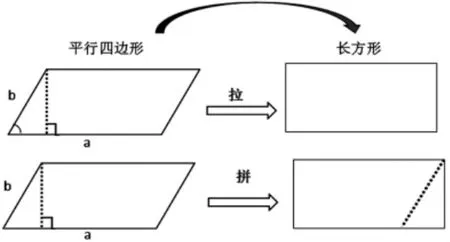
师：长方形和平行四边形之间有着怎样的关系呢？什么变了？什么没变？

生：底没有变化，高在变化，面积也在变化。

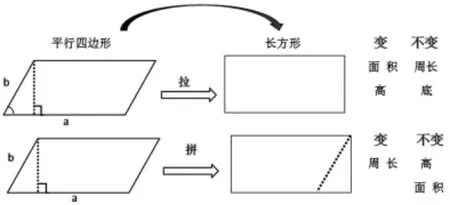
生：两条邻边的夹角也在发生变化。

师：现在你觉得平行四边形的面积还和什么有关系呢？

生：夹角。

师：两条邻边的夹角越大，面积——（越大）。同学们不仅善于观察，还很善于思考，你们说的都很有道理，随着我们学习的深入，以后求平行四边形的面积，用邻边也可以求出来，留给大家课后去思考、去探究。

【设计意图：从平行四边形一拉一拼中，引导学生思考什么变了？什么没有变？聚焦核心问题，让学生在观察中思考，探索平行四边形与转化后的长方形之间的联系，一是将今天学习的转化进行巩固，比较平行四边形和通过剪拼得到的长方形，底、高、面积、周长之间的联系与变化。二是将今天的拼与旧知的拉进行对比，讨论什么变了，什么没变，进一步思考平行四边形的面积与邻边的关系，将转化过程得到的不同数据综合在一幅图里进行初步归纳，明确平行四边形与转化成的长方形的内在联系。】