例谈判定正方形的三种方法

孟惠

正方形，不仅是特殊的平行四边形，而且 是特殊的矩形和菱形.对此，笔者从平行四边 形、矩形、菱形三个角度，总结了判定正方形 的常用方法，以期能够帮助同学们学以致用.

一、利用“平行四边形+一组邻边相等+一 个角为直角”判定

有一组邻边相等，且有一个角为直角的 平行四边形，被称为“正方形”.根据这一定 义，在证明一个四边形是否为正方形时，不妨 以平行四边形为切入点，先思考该四边形是 否为平行四边形，然后考虑它的一组邻边是否 相等，能否证明一个角为直角.若该四边形既是 平行四边形，又有一组邻边相等，且一个角为 直角，那么就可以判定该四边形为正方形.

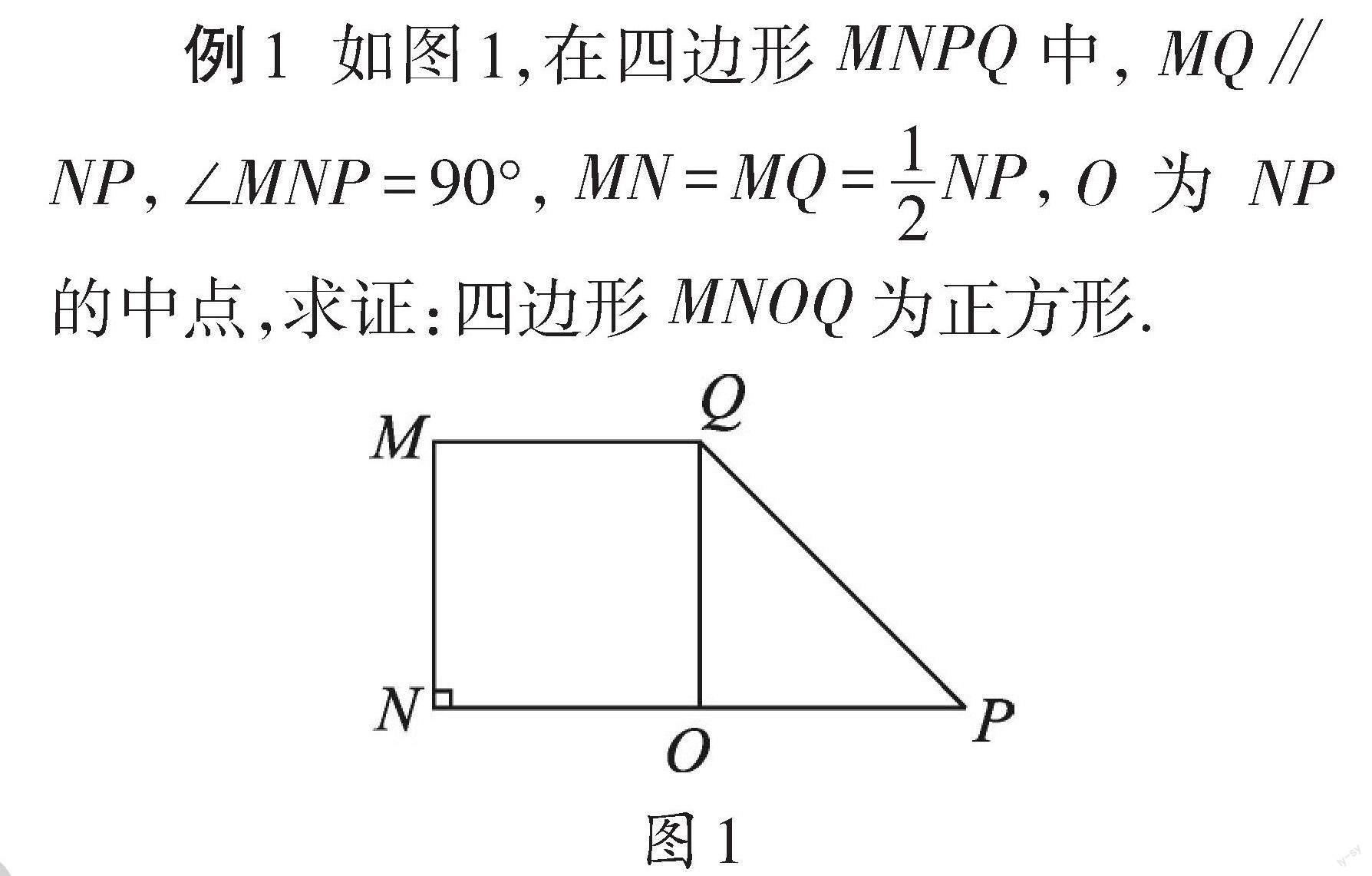
例1

分析：由题意可知，四边形 MNQP 中有 一组邻边相等，一个角为直角，因此，要证明 该四边形为正方形，只需要证明四边形 MNOQ 为平行四边形，且有一个角为直角即可.

证明：

评注：在证明一个四边形为正方形时，同 学们要从正方形的基本概念出发，借助“平行 四边形+一组邻边相等+一个直角”进行判定.

二、利用“矩形+一组邻边相等”判定

正方形也是邻边相等的矩形.在判定一 个四边形是否为正方形时，同学们还可以从 矩形的角度予以考虑，先对这个四边形是否 为矩形进行判定，再判断它是否有一组邻边 相等.若这个四边形为矩形，且有一组邻边相 等，那么此四边形必为正方形.

例2

分 析 ：由 题 意 易 知 △MAN、△NDP、△QCP、△MBQ 都为等腰直角形，这样就有 ∠MAN = ∠D = ∠PCQ = ∠B = 90°，易证得四边 形 ABCD 为矩形，只要再证明矩形 ABCD 中 有一组邻边相等，即可使问题得证.

证明：

评注：在证明一个四边形为正方形时，如 果该四边形为矩形，且有一组邻边相等，那么 这个四边形就是正方形.

三、利用“菱形+一个角是直角”判定

正方形的四条边都相等，四个角都相等 且都是直角.根据这一重要性质，在判定一个 四边形为正方形时，可先观察条件中是否蕴 含了几组相等的边，并由此先证明该四边形 为菱形，再证明它有一個角为直角，进而利用 “有一个角是直角的菱形为正方形”判定该四 边形为正方形.

例3 如图3，已知四边形 ABCD 和 BEFG 均为正方形，延长 BC 到点 M，在 AB 上任取一 点N，使得CM = BG = AN. 求证：四边形 DNFM 为正方形.

分析：本题由已知条件易证得△DAN≌ △NGF≌△MEF≌△DCM，易得到 DN = NF = FM = MD，进而证得四边形 DNFM 为菱形，这 样只要再证明菱形 DNFM 中有一个角为直 角，问题即可迎刃而解.

证明：

评注：在判定一个四边形为正方形时，同 学们除了考虑平行四边形、矩形外，还要注意 从菱形的角度去分析和解答问题.

当然，判定正方形的方法并不只有上述 提及的这三种，同学们在平时的学习中，要 注意掌握不同几何图形的定义、特点、性质 以及判定方法，多归纳总结，从而提高解题 能力.