四边形新定义问题例析

王 峥

⦿ 江苏省徐州市第十三中学

四边形新定义问题,是培养学生创造性思维的良好素材,包括“等邻边四边形”问题、“等角相邻点”问题、“妙线”问题、“准等距点”问题等.以下作一分析探讨,以飨读者.

1 “等邻边四边形”问题

菱形、正方形是四边都相等的四边形,它们都是从实际生活中抽象出来的,因为应用广泛而得到推广.“等邻边四边形”是指有两组邻边相等的凸四边形.“等邻边四边形”有什么性质?又如何判定呢?下面结合实例进行探讨.

例1我们定义:有两组邻边相等的凸四边形叫做“等邻边四边形”．如菱形、筝形都是特殊的“等邻边四边形”．

(1)如图1,四边形ABCD中,若∠ABC=∠BCD,BC∥AD,对角线BD恰巧平分∠ABC,则四边形ABCD______“等邻边四边形”.(填“是”或“不是” )．

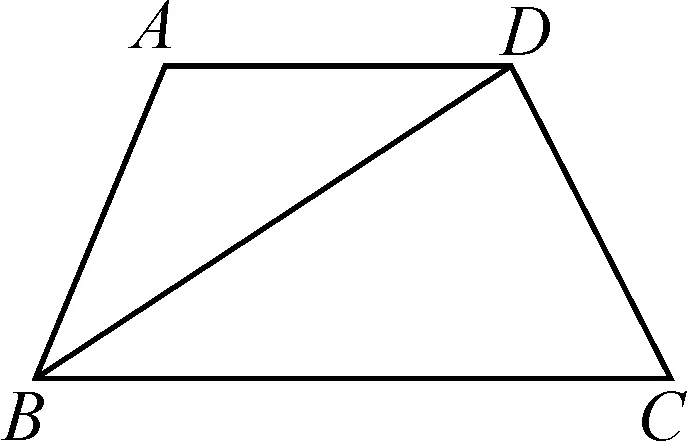
图1

(2)在探究“等邻边四边形”的性质时:

①小红画了一个“等邻边四边形”ABCD(如图2),其中AB=AD,BC=CD,若∠A=80°,∠C=60°,写出∠B,∠D的度数．

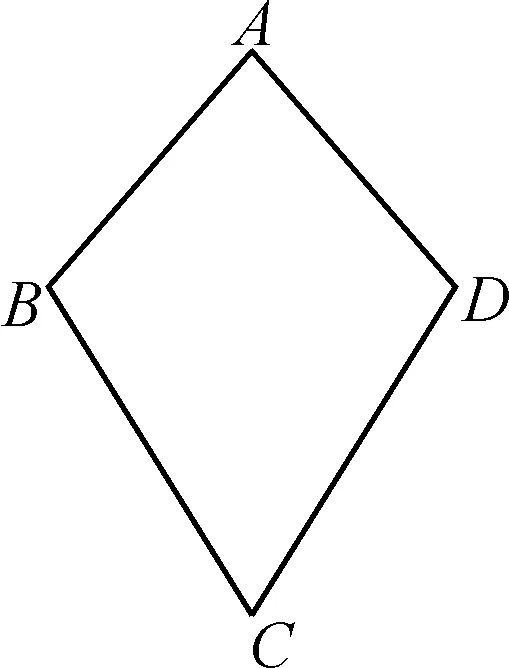
图2

②小红猜想:对于任意四边形,若有一组邻边相等,一组对角相等,则这个四边形为“等邻边四边形”.你认为他的猜想正确吗?若正确,请证明;若不正确,请举出反例．

(3)在锐角三角形ABC中,AB=AC,在平面内存在一点P,使PB=BA,PA=PC,四边形PABC可能是“等邻边四边形”吗?若可能,画出符合题意的图形,并求∠BAC的度数;若不可能,请说明理由.

解析：(1)由AD∥BC,∠ABC=∠BCD,可知四边形ABCD是等腰梯形,则AB=CD.

由∠ADB=∠DBC,∠ABD=∠DBC,得∠ABD=∠ADB,则AD=AB,AD=DC,所以四边形ABCD有两组邻边相等,即四边形ABCD是“等邻边四边形”.故填答案:是．

(2)①如图3,连接AC．因为AB=AD,BC=DC,AC=AC,所以△ABC≌△ADC(SSS),可得∠B=∠D.又∠BAD=80°,∠BCD=60°,则∠B+∠D=360°-80°-60°=220°.所以∠B=∠D=110°．

图3

②小红猜想错误．反例,如图4所示．四边形ABCD中,BA=BC,∠ABC=∠ADC=60°,四边形不是“等邻边四边形”．

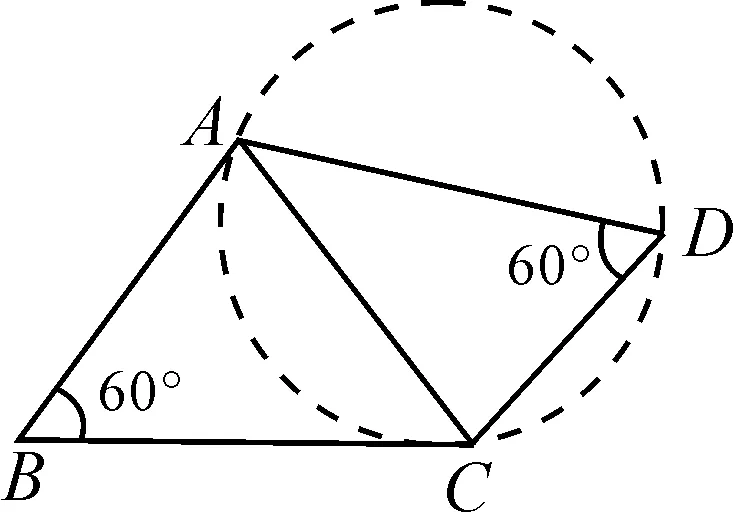
图4

(3)①如图5,当CB=CP时,由PA=PC,可知四边形ABCD是“等邻边四边形”．设BP交AC于点O.

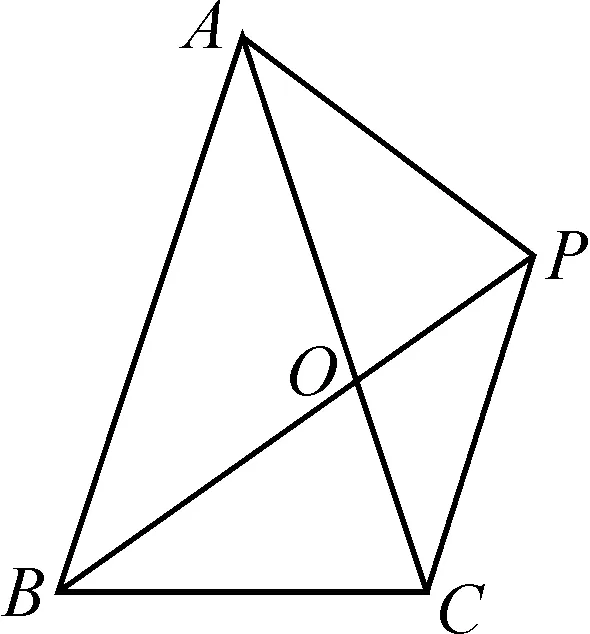
图5

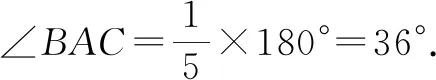
②如图6,当△ABC是等边三角形时,四边形ABCP是“等邻边四边形”．

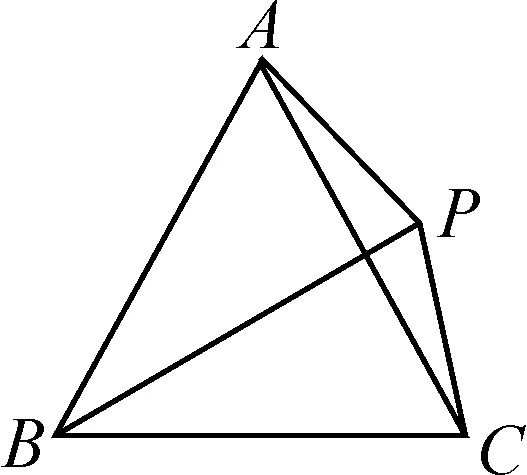
图6

综上所述,满足条件的∠BAC的值为36°或60°．

2 “等角相邻点”问题

平行四边形的对角线互相平分;菱形的对角线互相垂直平分;矩形的对角线相等且互相平分;正方形的对角线相等且互相垂直平分.这些实际上是对应四边形的中心点与四边形的关系,“等角相邻点”问题是指四边形内一点与其四个顶点连接,在四边形内形成的四个角中有两组角相等.那么,如何得到等角相邻点?等角相邻点又有什么性质呢?

例2如图7-1,在四边形ABCD内取一点P,连接AP,BP,CP,DP,如果∠APD=∠APB=α,且∠BPC=∠CPD=β,那么P叫做四边形ABCD的一个等角相邻点．

图7-1

(1)如图7-2,已知正方形ABCD,请在其内部找一点P,使P为等角相邻点,且α≠β;

图7-2

(2)如图7-3,已知任意四边形ABCD,请在其内部找一点P,且P为等角相邻点;

图7-3

(3)如图7-4,已知任意四边形ABCD,在它的内部有两个等角相邻点P1,P2,证明:线段P1P2上任意一点也是等角相邻点．

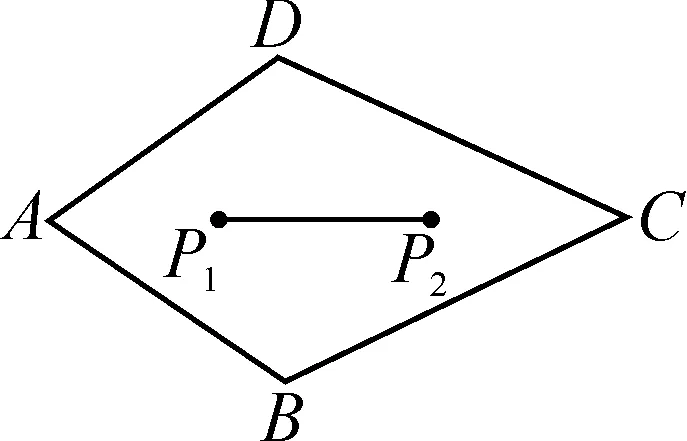
图7-4

解析：(1)如图8,所画的点P在AC上且不是AC的中点和AC的端点.

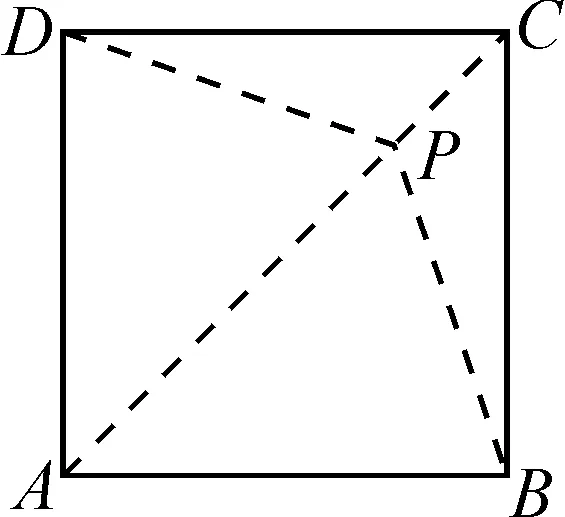
图8

(2)如图9,画点B关于AC的对称点B′,延长DB′交AC于点P,则点P即为所求.

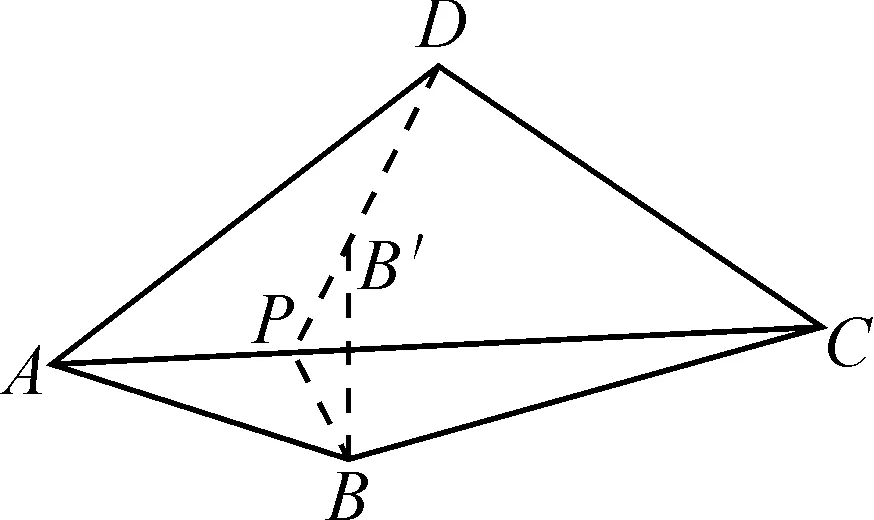
图9

图10

3 “妙线”问题

由于中心对称图形绕中心旋转180°后能与原图形重合,所以过中心对称图形对称中心的任一条直线,分中心对称图形成两部分,这部分的面积是相等的.但是对于任意四边形,如何画一条直线把它分成面积相等的两部分呢?下面结合实例对此进行深入的讨论,并将这样一条直线称为“妙线”.

例3我们把能将四边形分成两部分,且这两部分的面积相等,这样的直线称为“妙线”．下面的图示,是得到“妙线”的过程:如图11,在四边形ABCD中,取对角线BD的中点O,连接OA,OC,显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于点E,则直线AE即为一条“妙线”．

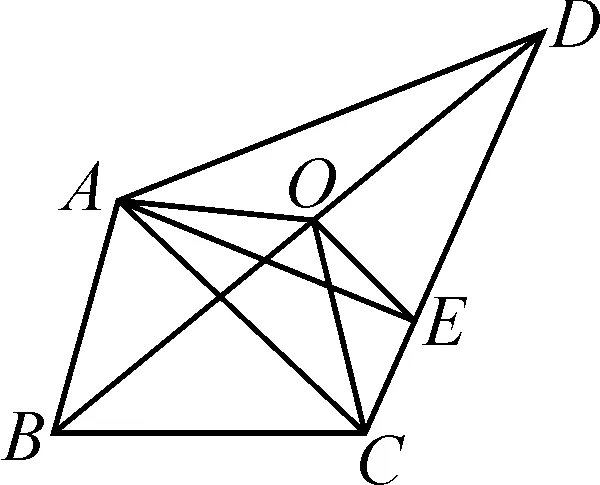
图11

(1)如图11,试说明直线AE是“妙线”的理由;

(2)如图12,AE为一条“妙线”,F为AD边上的一点,请作出经过点F的“妙线”,并说明理由;

图12

(3)如图13,已知一块土地是五边形ABCDE,经过开发,又得到多边形EDCMN,中间的折线CDE是一条小路,现要修一条直路,且这条直路经过点E,使直路右边的面积不作改变,如何画图呢?

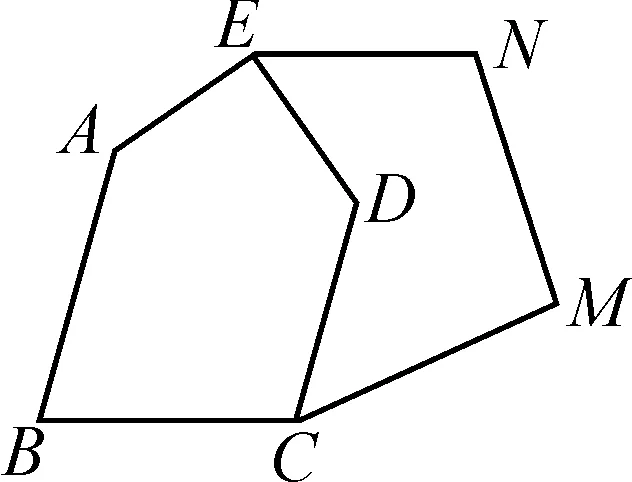
图13

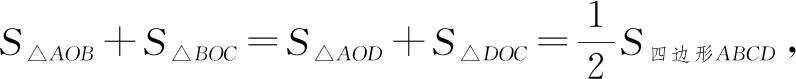
图14

(2)如图15,连接EF,过点A作EF的平行线交CD于点G,连接FG,则GF为一条“妙线”．

图15

理由:由AG∥EF,可知S△AGE=S△AFG．设AE与FG的交点是O,则S△AOF=S△GOE.又AE为一条“妙线”,所以GF为一条“妙线”．

(3)如图16,连接CE,过点D作DF∥EC交CM于点F,连接EF,则EF为所修的直路.

图16

本文中从形到点再到线,对四边形内存在的特殊四边形、特殊点、特殊线作了深入细致的研究,得到了一些创造性的结论,开阔了学生的认知视野,培养了学生创新解决问题的能力,是四边形领域里一道亮丽的风景线.Z