矩阵方程的三对角中心对称最小二乘解

张 翔， 王卿文

(1.上海大学理学院，上海200444;2.遵义师范学院数学系，贵州遵义563000)

本研究中，Rm×n代表所有 m×n阶实矩阵，ORm×m代表所有正交m×m阶矩阵，Ik表示k阶单位矩阵，‖.‖表示矩阵的Frobenius模.由于很多工程和电子信息问题都需要解决矩阵的逆问题，即给定A，B∈Rm×n，寻求m×m阶实矩阵X，使得XA= B［1-3］.根据问题的不同需要，存在不同类型的解X.三对角中心对称矩阵的结构较一般对称矩阵更复杂，并且关于三对角中心对称解的研究也很少见.但是三对角中心对称矩阵在噪音处理、工程技术等方面有着重要应用［4-10］.因此，本研究考虑在给定A，B∈Rm×n的情况下，寻求n×n阶实三对角中心对称矩阵X，使得‖AX-B‖最小.

1 定义及初步结果

定义1 如果A=(aij)∈Rn×n是中心对称的，且为三对角矩阵，则该矩阵为三对角中心对称矩阵，记作CSTRn×n.

引理1［4］(1)如果X为2k×2k阶实三对角中心对称矩阵，则X可表示为

(2)如果X为(2k+1)×(2k+1)阶实三对角中心对称矩阵，则X可表示为

在式(1)，(2)中，M为k×k阶实三对角中心对称矩阵，Sk=(ek，ek-1，…，ei，…，e1)，ei为Ik的第i列，u∈Rk×1，且u=(0，0，…，b)T，a，b为实数.

引理2［4］(1)如果n=2k，令

则所有的实2k×2k阶三对角中心对称矩阵X可表示为

(2)如果n=2k+1，令

则所有的实(2k+1)×(2k+1)阶三对角中心对称矩阵X可表示为

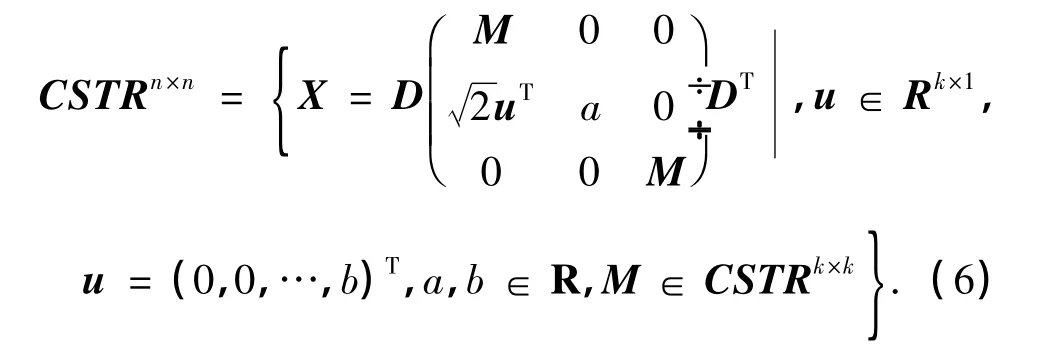
2 定理及其证明

文献［5］列出了当n为偶数时本问题的解和最小二乘解.为保证定理的完整性，在此仅列出n为偶数的情况，而主要论证n为奇数的情形.

定理1 (1)如果n=2k+1，假设A，B∈Rm×n，AD=(A1，A2)，BD=(B1，B2)，其中 A1，B1∈Rm×(k+1)，A2，B2∈Rm×k，则矩阵方程AX=B存在三对角中心对称解当且仅当

其中

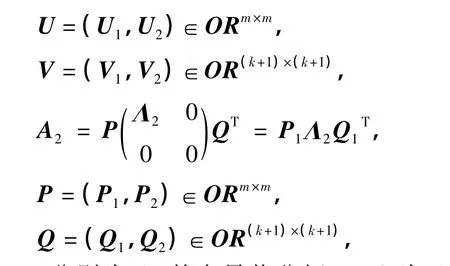
式中，U，V分别为A1的奇异值分解，P，Q为A2的奇异值分解，并且

(2)如果n=2k，假设A，B∈Rm×n，AD=(A1，A2)，BD=(B1，B2)，其中 A1，B1∈Rm×k，A2，B2∈Rm×k，则矩阵方程AX=B存在三对角中心对称解当且仅当

其中

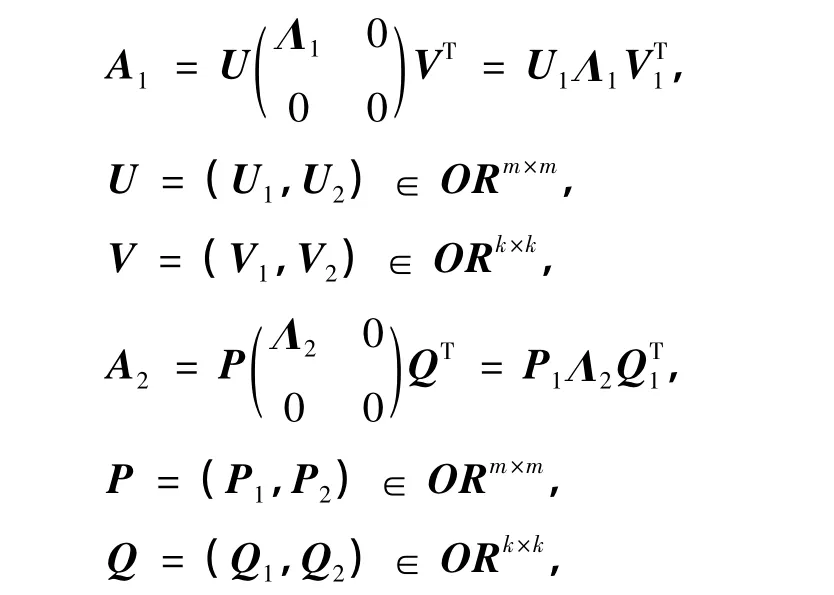
式中，U，V为A1的奇异值分解P，Q为A2的奇异值分解.

证明 由Frobenius模的正交不变性，有

注意到AX=B与‖AX-B‖=0等价，因而，AX=B存在三对角中心对称解当且仅当

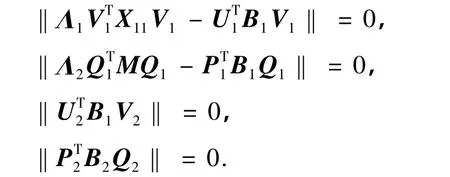
即证.

定理2 (1)如果n=2k+1，假设A，B∈Rm×n，AD=(A1，A2)，BD=(B1，B2)，其中 A1，B1∈Rm×(k+1)，A2，B2∈Rm×k，则存在三对角中心对称矩阵X，使得‖AX-B‖最小的充分必要条件为

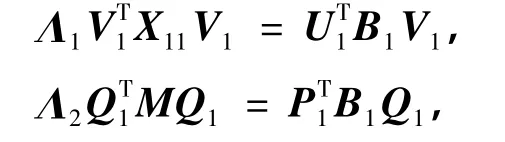
式中，Λ1，Λ2，U1，V1，P1，Q1，X11同定理1.

(2)如果n=2k，假设A，B∈Rm×n，AD=(A1，A2)，BD=(B1，B2)，其中A1，B1∈Rm×k，A2，B2∈Rm×k，则存在三对角中心对称矩阵X，使得‖AXB‖最小的充分必要条件为

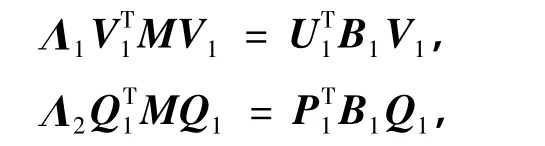
式中，Λ1，Λ2，U1，V1，P1，Q1同定理1.

证明 由定理1的证明可得，存在三对角中心对称矩阵X，使得‖AX-B‖最小的充分必要条件为

［1］ SUNL G.Two kinds of inverse eigenvalue problems for real symmetric matrices［J］.Math Numer Sinica，1988 (3)：282-290.

［2］ LIN.A matrix inverse eigenvalue problem and its application［J］.Linear Algebra Appl，1997，266：143-152.

［3］ BOLEYD，GOLUBG H.A survey of matrix inverse eigenvalue problems［J］.Inverse Problem，1987(3)：595-622.

［4］ XUZ，ZHANGK，LIUQ.Fast algorithms of Toeplitz form［M］.Xi’an：Northwest Industry University Press，1999.

［5］ ZHANGX，WANGQ W.The centrosymmetric tridiagonal least square solution to a matrix equation［C］∥ The Third International Workshop on Matrix Analysis and Applications.2009：83-85.

［6］ ZHOUB，LIZ Y，DUANG R，et al.Weighted least squares solutions to general coupled Sylvester matrix equations［J］.Journal of Computational and Applied Mathematics，2009，224：759-776.

［7］ ZHANGZ Z，HUX Y，ZHANGL.Least-squares solutions of inverse problem for hermitian generalized Hamiltonian matrices［J］.Applied Mathematics Letters，2004，17：303-308.

［8］ SUNC G.Parallel solution of sparse linear least squares problems on distributed-memory multiprocessors［J］.Parallel Computing，1997，23：2075-2093.

［9］ LIZ Y，WANGY，ZHOUB，et al.Least squares solution with the minimum-norm to generalmatrix equations via iteration［J］.Applied Mathematics and Computation，2010，215：3547-3562.

［10］ LIUZ Y，TIANZ L，TANY X.Computing the leastsquare solutions for centrohermitian matrix problems［J］.Applied Mathematics and Computation，2006，174：566-577.