具有连续相位调制特性的甚小线性调频键控信号分析

姜俊超， 郑国莘， 邱志易， 刘雅君

(上海大学通信与信息工程学院，上海200072)

通信系统的性能在很大程度上由调制方式所决定.为了在带宽上获得较高的传输速率，调制需满足较高的频谱利用率及较小的旁瓣等特性.超窄带调制方式一经提出就以其高效的频谱利用率而广受关注.与传统的调制方式如频移键控(frequency shift keying，FSK)、幅移键控(amplitude shift keying，ASK)等相比，超窄带(ultra narrow band，UNB)通信体制能够在相同数据传输速率下，只占用前者几分之一的带宽［1］，因而，能够有效地提高通信体制的频带利用率.

至今，超窄带体制已经提出了一系列调制方式，包括 Walker［2］提出的甚小线性调频键控(very minimum shift keying，VMSK)调制方式和吴乐南［3-4］提出的甚小波形差键控(very-minimum waveform difference keying，VWDK)调制方式等.本研究提出的甚小线性调频键控(very minimum chirp keying，VMCK)调制方式［5-6］，是在一个比特周期内采用升频或降频的线性调制来构成二元信号，具有更窄的带宽和旁瓣衰减程度，从而愈加受到关注.

目前，许多针对VMCK调制方式的相关研究，包括波形调制时去除VMCK信号的直流分量［6］、通过波形优化的方式去除其旁瓣频谱处的离散谐波分量［7］、采用多进制的二次甚小线性调频键控(quadrate very minimun chirp keying，QVMCK)调制方式［8］、VMCK信号的正交性、VMCK在无线信道传输中的误码率分析［9］等，均采用了发送随机二进制数字序列的方法来分析VMCK频谱.

1 VMCK调制的连续相位特性

VMCK信号在单周期t∈［0，T］时间内的波形表达式为

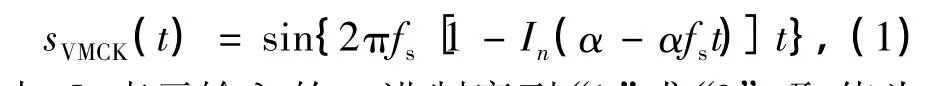
式中，In表示输入的二进制序列“1”或“0”，取值为+1或-1，0＜α≤1，0＜t≤1/fs.由于VMCK调制是一种连续相位调制，故可以从连续相位调制(continuous phase modulation，CPM)的一般表达式中通过确定相应参数来推导出VMCK信号.

CPM作为一种典型的恒包络连续相位调制方式，能够实现较窄的频谱主瓣和较低的谐波分量谱，从而提高了信号的频谱利用率［10］.根据调制系数h和积分脉冲g(t)的不同，CPM调制技术至今已包含多种分类，如最小频移键控(minimum shift keying，MSK)、正弦频移键控(sine frequency shift keying，SFSK)、连续相位频移键控(continuous phase frequency shift keying，CPFSK)等.通常，CPM信号的一般波形表达式为

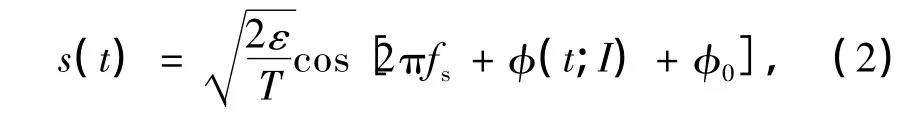
式中，ε为信号码元能量，T为码元间隔宽度，fs为载频，φ0为载波的初始相位，φ(t;I)表示调制信息的时变相位函数.在式(2)中确定特定参数，就可以推导出VMCK的表达式，首先分析式(2)所示CPM信号的时变相位函数：

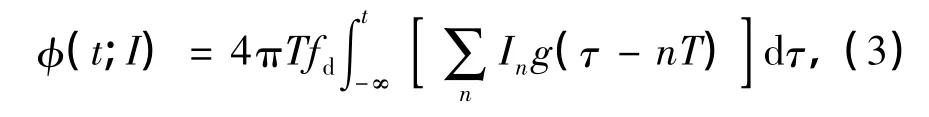
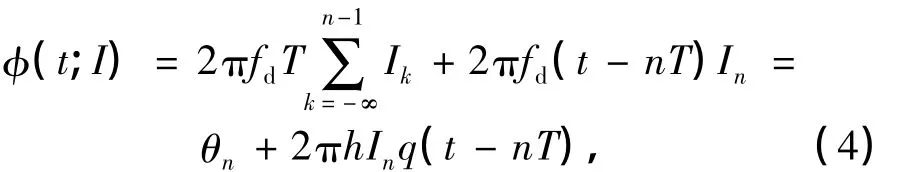
不同于常规的积分脉冲，VMCK调制中创新性地选用一种随时间t呈线性变化的g(t)为积分脉冲，如图1(b)所示，其表达式为

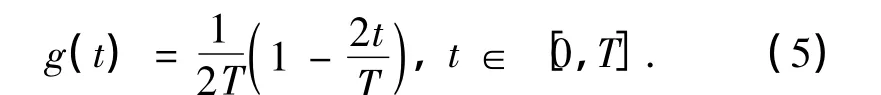
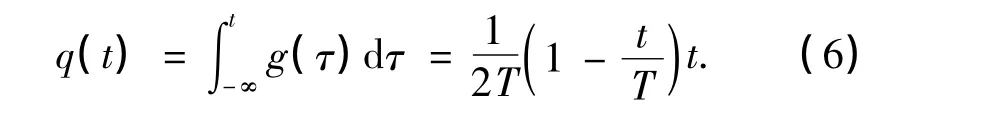
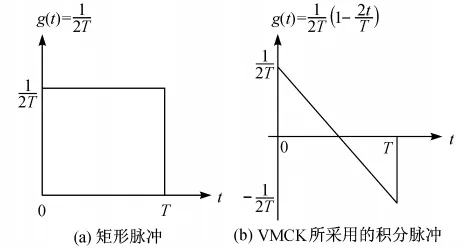
图1 积分脉冲g(t)的时域波形Fig.1 Time-domain waveforms of integral pulse g(t)

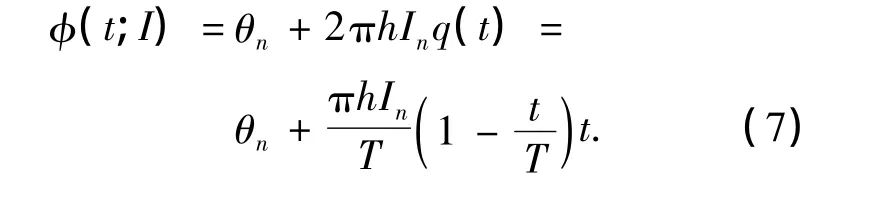
在t∈［0，T］情况下，将式(6)代入式(4)，可以得到VMCK的时变相位函数的表达式为由式(7)易知：当t=0时，φ(t;I)=θn;当t=T时，φ(t;I)=θn.因而不论In取值如何变化，在一个码元周期内，相位函数φ(t;I)始终保持连续变化，并且在整个码元周期内的改变值为0，可见VMCK符合连续相位调制特性.

在确定了VMCK时变相位函数φ(t;I)的表达式之后，将其代入式(2)，并设定波形幅度A=1，初始相位φ0=-π/2，且fs=1/T，则可得

最后，需要确定调制系数h.由式(1)可知，对于VMCK信号而言，其可达到的最大角频率偏移Ωmax=2π·2αfs，则按照定义可得

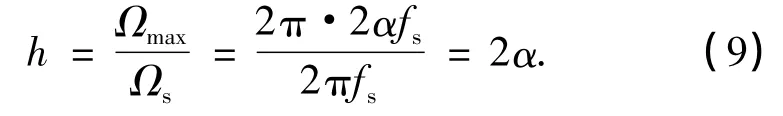
至此，我们已确定了由式(2)所示的CPM一般表达式推导至VMCK过程中所需确定的所有参数，将h=2α代入式(8)，可得

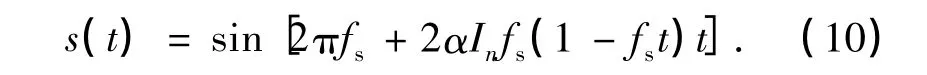
可以看到，当In取+1或者-1时，式(10)的结果与式(1)所示的VMCK表达式一致.这表明VMCK信号可作为一种连续相位调制.

2 VMCK调制的发射机结构

对于VMCK信号的调制，通常根据所发送的二进制序列“1”或“0”，分别进行调制后相加以实现其发射机结构，如图2所示.

图2 VMCK发射机结构Fig.2 Transmitter structure of VMCK

而基于连续相位的观点，可对VMCK时域表达式作进一步分析：

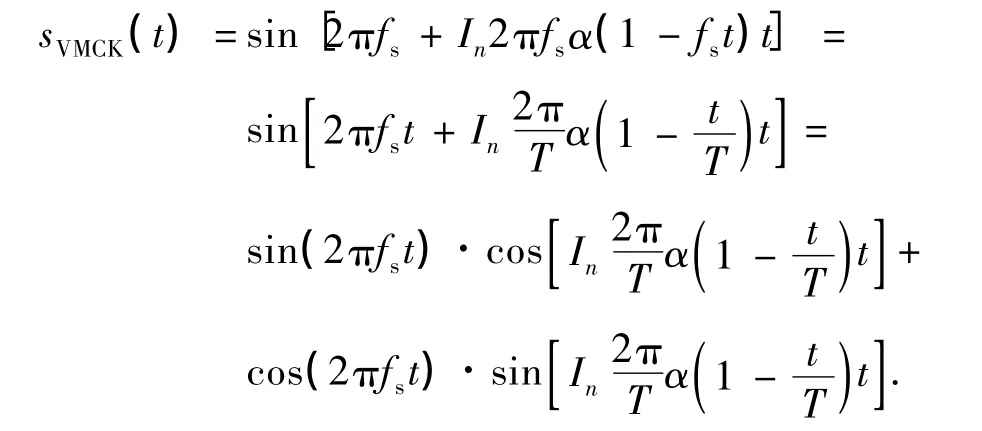
另外，由于cos(Inx)=cos x，sin(Inx)=Insin x，上式可进一步化简为

根据式(11)的结果，也可以通过如下步骤来实现二进制VMCK信号的调制［12］：

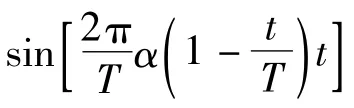
步骤2 将第一路和第二路数据分别对正交的载波cos(2πfst)与sin(2πfst)进行双边带调幅，如图3所示.

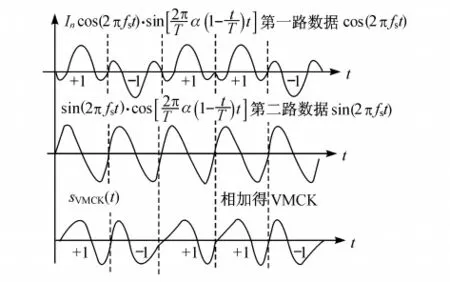
图3 VMCK的调制波形Fig.3 Modulation waveform of VMCK

步骤3 将步骤2中所得的两路正交的双边带信号叠加后形成VMCK信号.

根据上述的步骤，可以得到一种新型的VMCK调制的发射机结构，如图4所示.

图4 新型的VMCK发射机结构Fig.4 New transmitter structure of VMCK

这种新型的发射机结构只需要由直接数字频率合成(direct digital frequency synthesis，DDS)模块结合D/A模块即可完成调制，而无需对“1”，“0”信号进行分别调制，简化了发射机结构.

3 二进制VMCK信号功率谱分析

为了方便对二进制sVMCK(t)信号进行功率谱分析，我们定义v(t)为信号sVMCK(t)的等效低通信号，其表达式为

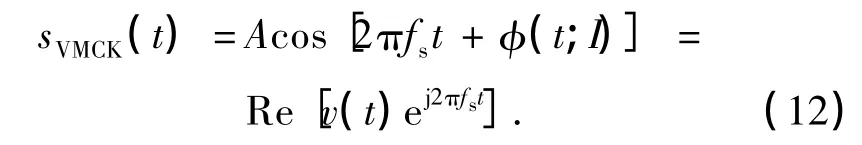
那么易知

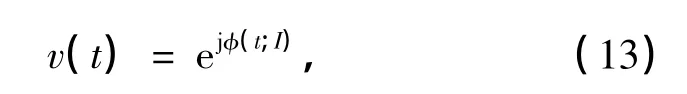
则s(t)和v(t)二者功率谱密度之间的关系为

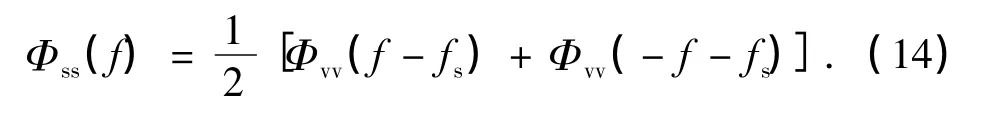
因而，要得出信号sVMCK(t)的功率谱密度，只需确定其等效低通信号v(t)的自相关函数和功率谱密度即可.由于发送序列{In}为二进制序列，并且其中的每一个符号都是统计独立和同分布的，而积分脉冲g(t)=q'(t)在［0，T］之外的值为0，所以求得v(t)的自相关函数为

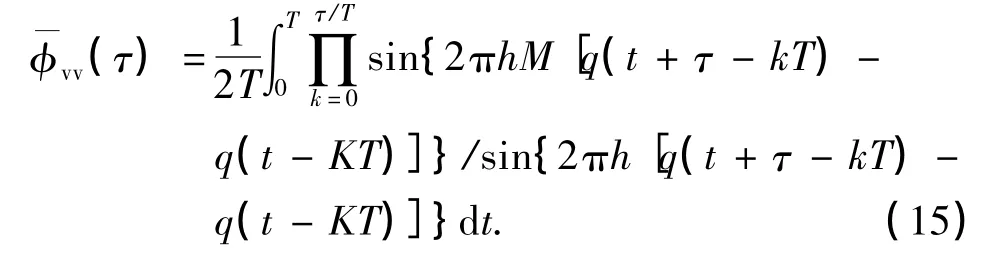
对式(16)作傅里叶变换，得到其对应的功率谱密度表达式为

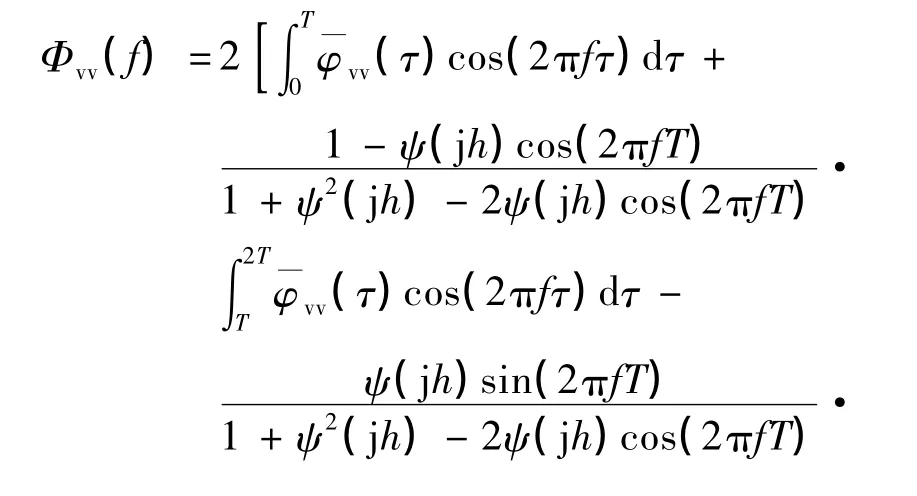
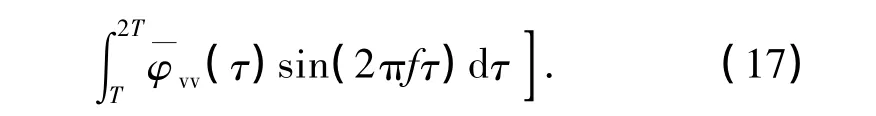
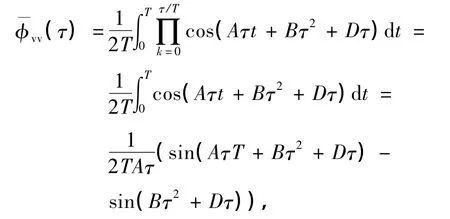
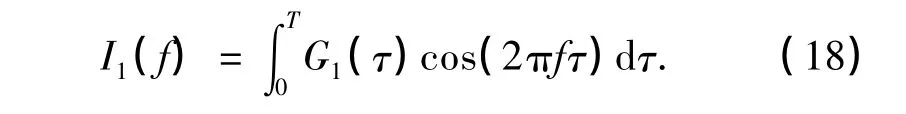
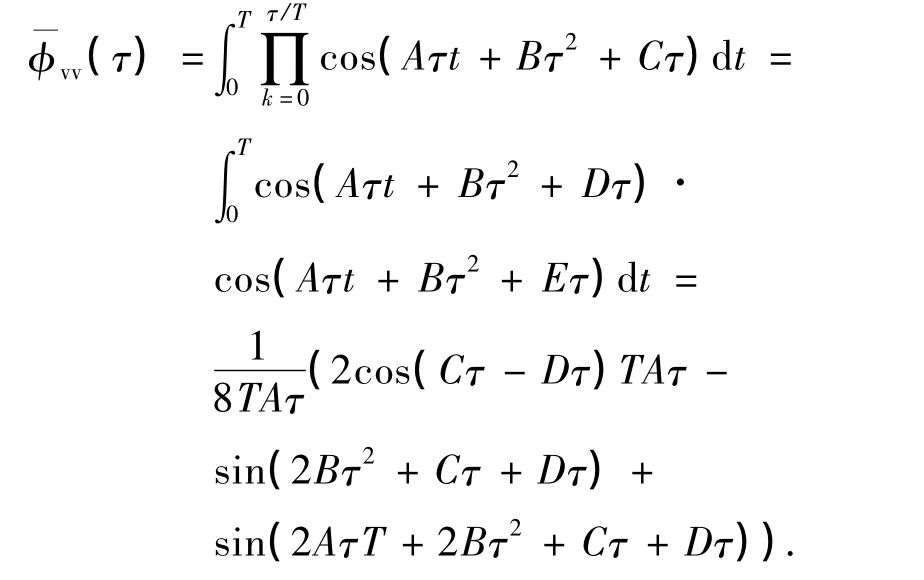
将其表示为G2(τ)，则可定义

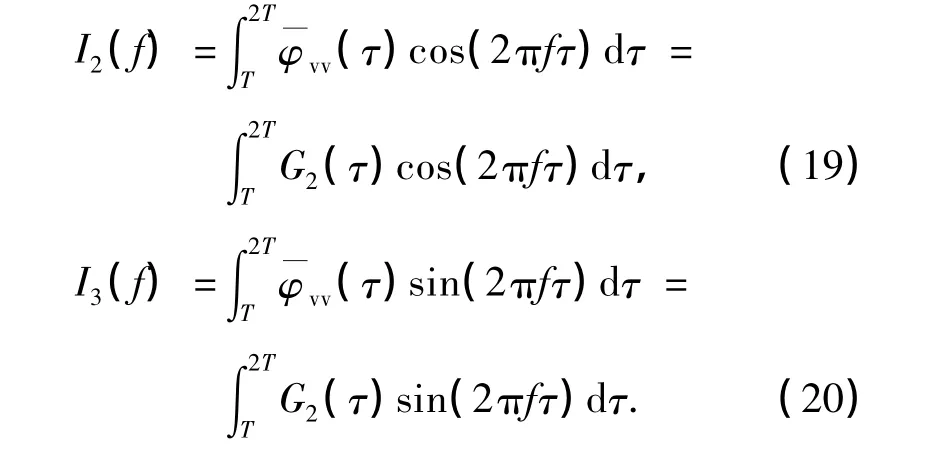
由于调制系数h=2α，进制值M=2，定义常数

则最终Φvv(f)可化简为如下表达式：

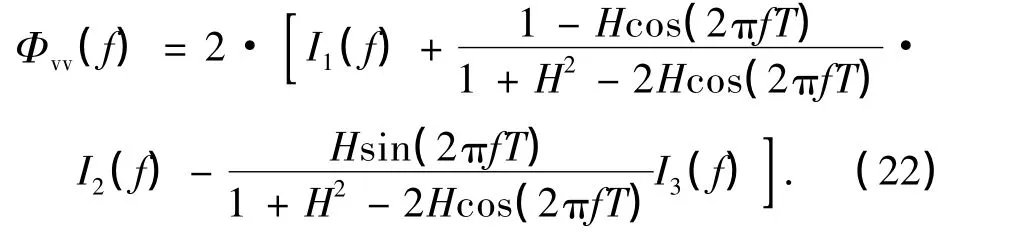
图5是根据式(22)在不同调制系数h=2α情况下的VMCK信号归一化功率谱图，并与MSK信号作对比.

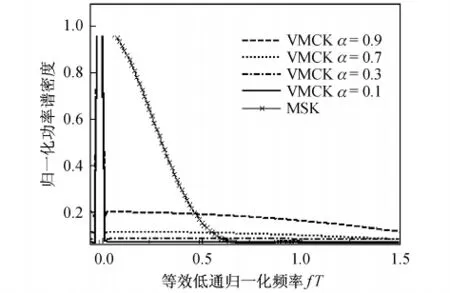
图5 不同调制系数α情况下等效低通VMCK归一化功率谱密度Fig.5 Equivalent low-pass normalized power spectral densityofVMCK in differentmodulation factor α

图5分别给出了调制系数α=0.9，0.7，0.3和0.1时，二进制等效低通VMCK信号的功率谱密度，其中横坐标为归一化频谱fT，即横坐标零点处所对应的载频f=fs.可以看到，VMCK的频谱能量主要集中于载频fs周边的一个很窄的带宽之内，并且随着调制系数α的降低，其信号旁瓣的功率谱也呈下降态势，这种频谱特性也表明了VMCK调制具有相当窄的传输带宽，因而调制信号的频带利用率也进一步得到提高.

4 VMCK与MSK信号功率谱比较

对于MSK信号而言，其代表“1”和“0”的2个波形信号具有如下相关系数：

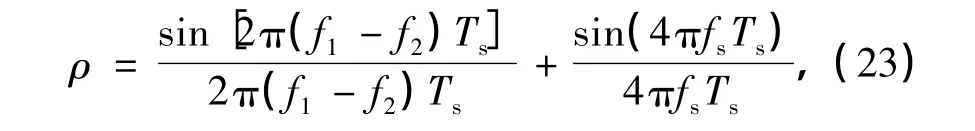
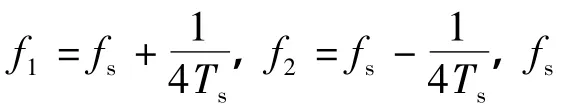
而对于VMCK调制而言，当调制系数α=0.7时［5］，其二进制信号的互相关系数同样也为ρ=0，这也就表明了在α=0.7的情况下，VMCK信号也是一种正交调制.因而在调制信号正交的情况下，MSK和VMCK在解调时的误码率Pe与信噪比Eb/n0的关系均为

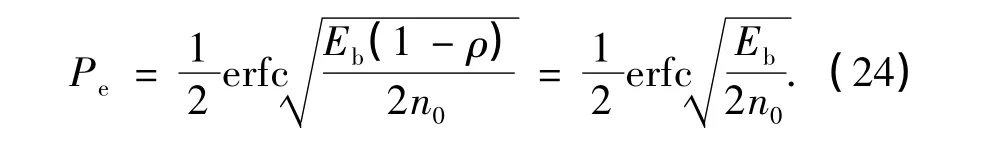
这就意味着MSK和VMCK(α=0.7时)在相同信噪比情况下有着相同的解调误码率.为了进一步比较这2种正交调制方式下的信号功率谱密度，我们设定二者的数据传码率相同，通过快速傅里叶变换计算二者的功率谱，并对其进行幅度归一化，如图6所示.可以直观地看出，VMCK(正交调制α=0.7时)的频谱能量主要集中在一个类似于冲击函数的单谱线内(即载频fs处)，其余频谱分量处明显低于载频，并且其旁瓣功率下降较快;而MSK信号的频谱能量在主瓣处较为集中，但相比VMCK的线频，MSK在主瓣处明显占用了更多的带宽，并且其旁瓣功率的衰减速度也不如VMCK来得迅速.

图6 二进制VMCK与MSK功率谱对比Fig.6 Compared power spectrum of binary VMCK with the MSK

为定量分析MSK和VMCK信号，图7给出了二者在VMCK调制系数α从0.2～0.8之间变化的5种情况的百分比功率带宽对比.

从图7可以看出，MSK信号的功率谱主要集中在0.6fs频带范围之内，越靠近载频处，MSK功率谱密度越大，而随着频率逐渐远离载频处，其功率谱密度下降较为平和.而VMCK在载频f=fs周边一个极窄的带宽内所占有的功率谱能量占整个频域能量很大的比重，并且随着频率逐渐远离载频处，其功率谱密度瞬间急剧下降，这就意味着VMCK的大量频谱能量集中在载频周围的一个极窄的频带范围内，因而具有明显的超窄带调制特性.

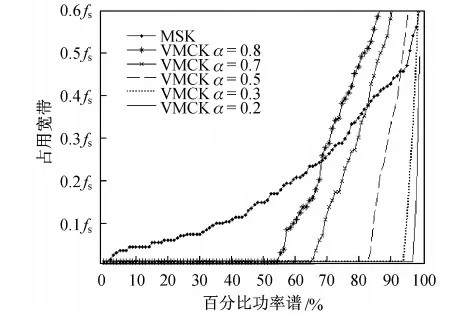
图7 VMCK和MSK百分比功率带宽比较Fig.7 Compared power percentage bandwidth of VMCK with the MSK

由图7还可以看到，伴随着VMCK信号调制系数α的减小，其在相同百分比功率谱情况下所占用的带宽也变窄，主要是因为随着α减小，其旁瓣功率衰减将越为迅速.如当α=0.3时，整个VMCK信号90%的功率谱密度几乎都集中在载频处，这也就意味着VMCK信号在频域上90%的能量都集中在靠近载频的极窄的带宽内，而MSK的90%的功率谱带宽约为0.4fs，这就体现出了VMCK信号在频带利用率上的优势.但是，当α选取较小数值时，二元信号的互相关系数将大于0，致使系统的抗噪性能下降.

考虑到VMCK解调端选用相干解调，因此，仍选用VMCK正交调制时α=0.7的情况［5］与MSK进行定量对比.此时，VMCK调制和MSK调制在相同的信噪比情况下具有相同的误码率.从图6中可以看出，在采用低于75%的功率谱百分比情况下，VMCK信号(正交时α=0.7)的带宽明显小于MSK信号，体现出了其作为超窄带通信调制方式的窄带特性.而当选用较大的功率百分比时，MSK信号带宽则小于VMCK信号.

5 结束语

本研究对CPM一般公式中的积分脉冲g(t)与调制系数h进行选定，把传统CPM中的积分脉冲由矩形脉冲或升余弦脉冲改变成随时间t呈线性变化的形式，推导出了具有相位连续特性的VMCK超窄带调制表达式.通过对VMCK信号的表达式的分析，给出了一种新型的调制步骤和发射机结构，其具有调制信号在单一路径的特点，有利于简化结构.此外，通过自相关函数傅里叶变换得到VMCK的功率谱密度解析表达式具有一般性.据此，对VMCK等效低通信号的功率谱密度与MSK调制方式对比，发现当功率百分比小于75%时，VMCK具有较高的频带利用率，可以适用于某些“见缝插针”的通信场合.

［1］ WALKERH R.Ultra narrow band modulation textbook［EB/OL］.［2009-12-09］.http：∥www.vmsk.org/ Textbook.pdf.

［2］ WALKERH R.VPSK and VMSK modulation transmit digital audio and video at 15 bits/sec/Hz［J］.IEEE Transactions on Broadcasting，1997，43(1)：96-103.

［3］ SAYHOODK H，WUL N.Raise bandwidth efficiency with sine-wave modulation VMSK［J］.Microwaves and RF Mag，2001，40(4)：79-84.

［4］ 吴乐南.超窄带高速通信进展［J］.自然科学进展，2007，17(11)：1467-1473.

［5］ ZHENGG X，FENGJ Z，JIAM H.Very minimum chirp keying as a novel ultra narrow band communication scheme［C］∥ICICS.2007：238-241.

［6］ ZHENGG X，YANGW Y，HEH，et al.Non DC offset very minimum chirp keying modulation as a novel ultra narrow band communication scheme［C］∥ CCWMSN07 Proceeding.2007：755-758.

［7］ 贾东立，郑国莘，张立，等.甚小线性调频键控调制波形的正弦基拟合优化［J］.上海大学学报：自然科学版，2010，16(4)：331-335.

［8］ JIW L，ZHENGG X，BAOM Q.Ultra-narrowband wireless communication technology based on QVMCK modulation［C］∥Proceeding of 2008 China-Japan Joint Microwave.2008：185-187.

［9］ BAOM Q，ZHENGG X，JIW L.BER performance analysisofultra-narrowband wireless communication technology based on VMCK modulation［C］∥Proceeding of China-Japan Joint Microwave.2008：193-196.

［10］ 冯思泉.连续相位调制(CPM)技术研究［D］.昆明：昆明理工大学，2007.

［11］ 孙明，林君，陈祖斌，等.基于DDS技术的chirp信号产生系统［J］.佛山科学技术学院学报：自然科学版，2004(4)：22-24.

［12］ 孙锦华，李建东，金力军.连续相位信号的调制及解调方法：中国，CN1710898［P］.2005-12-21.