二维Poisson方程的Legendre Tau方法的误差估计

沈婷婷， 马和平

(上海大学理学院，上海200444)

谱方法作为数值求解偏微分方程的有效工具之一，近年来得到了广泛的应用.根据选取检验函数的不同，谱方法可分为Galerkin方法、tau方法和配置法.关于Galerkin方法和配置法的一些理论分析和数值计算结果可参见文献［1-3］.本研究主要讨论tau方法在二维问题中的收敛性态.

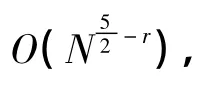
文献［12］虽然给出了Legendre tau方法求解一维二阶微分方程的L2模的最优误差估计，但对于高维情况下的收敛结果却没有具体讨论.由于tau方法在高维情况下仅有次优的误差估计，因此，本研究对于高维情况下 tau方法的收敛性态更感兴趣.

本研究考虑二维Poisson方程的Dirichlet问题，即

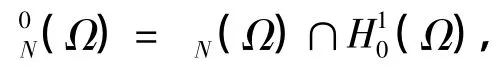
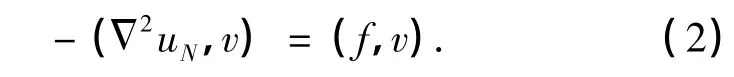
本研究主要目的是证明Legendre tau方法对于求解二维Poisson方程Dirichlet问题具有H1模和L2模的最优误差估计.文献［12］取类似(1-x2)-1uN作为检验函数，其中uN∈(I)，I=(-1，1).本研究将该方法应用到二维的情形.

1 基本引理

对任意的u∈H2(Ω)，v∈L2(Ω)，定义双线性形式为

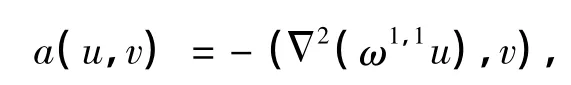
引理1 对任意的u∈H2(Ω)，v∈H1(Ω)，存在常数C，使得

证明 由文献［2］中的结论，得到

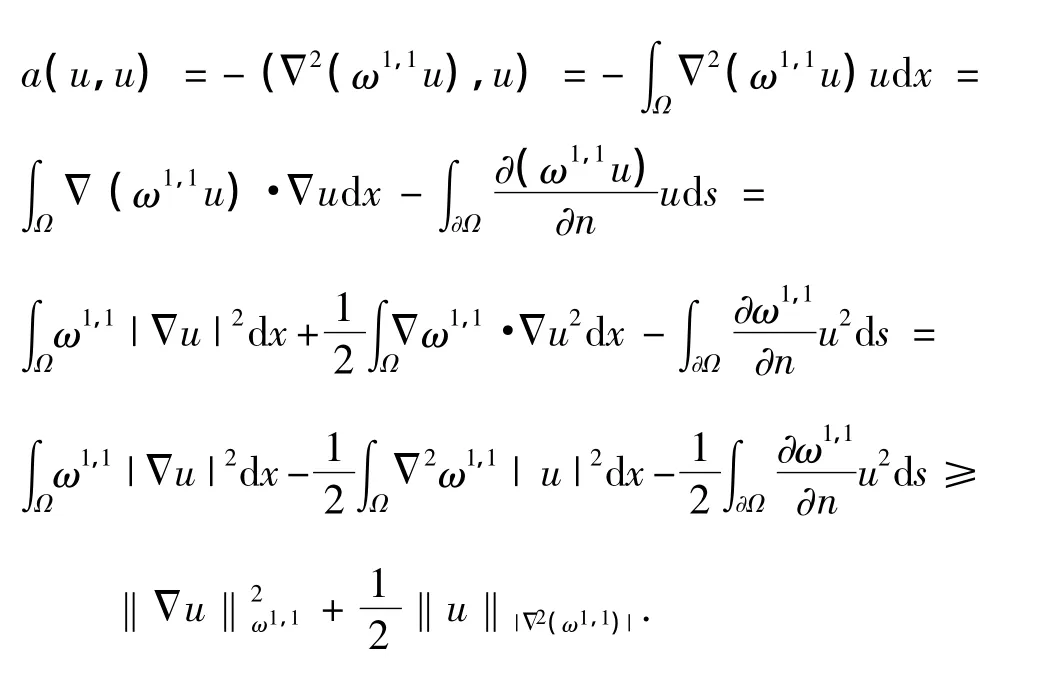
另一方面，有

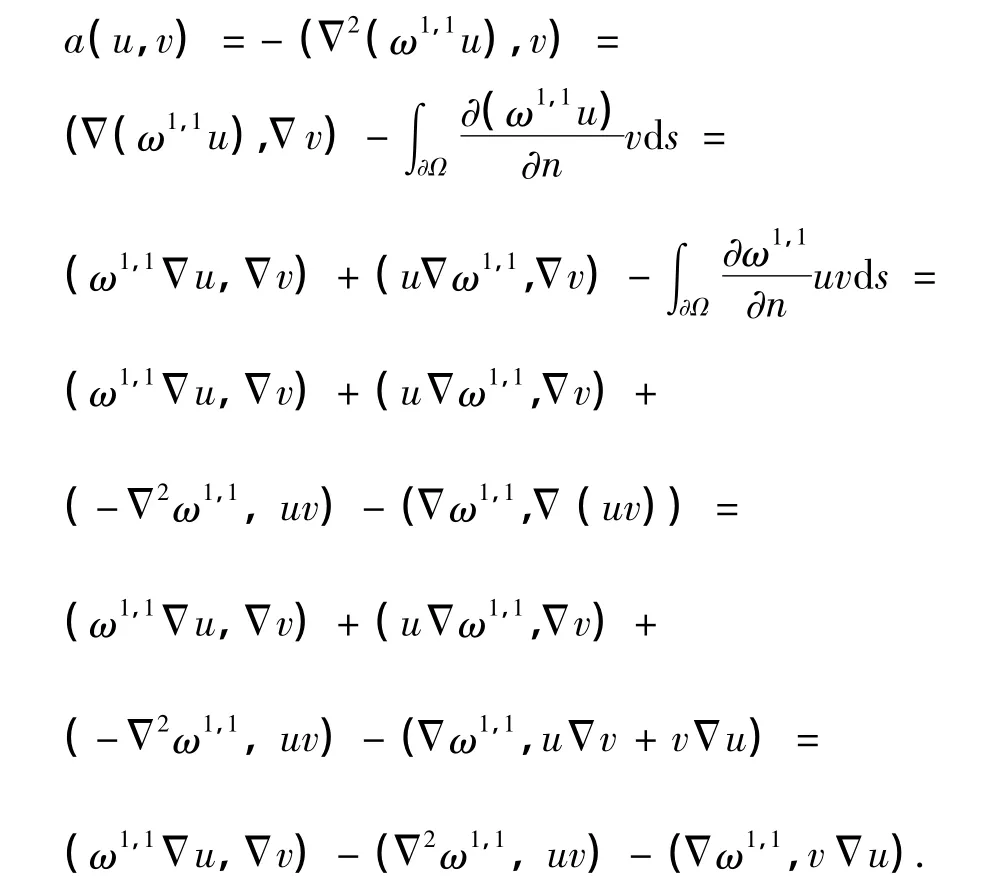
因此，

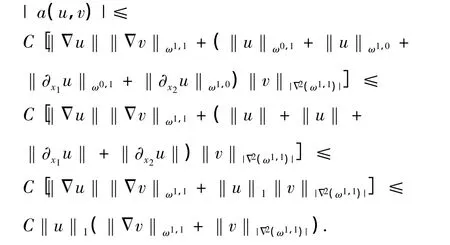
如果考虑对u，v∈H1(Ω)定义a(u，v)(弱形式)，则同样可以得到以上结果.

下面引入2个正交投影算子.

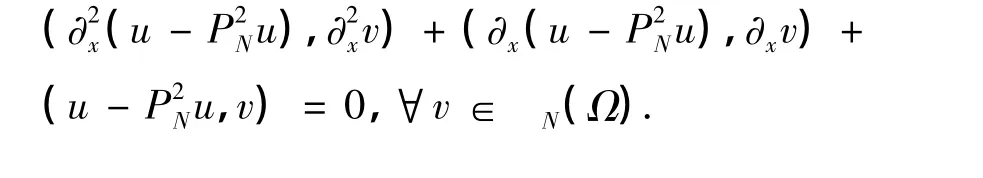
引理2［1］如果 u∈Hr(Ω)，且0≤l≤2≤r，则有

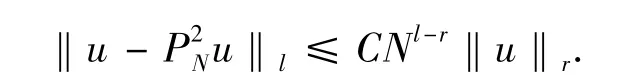
引理3［1］如果u∈Hr(Ω)∩H10(Ω)，且0≤l≤1≤r，则有

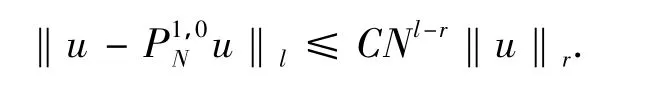
2 收敛性分析

由式(1)和(2)，可以得到如下误差方程：

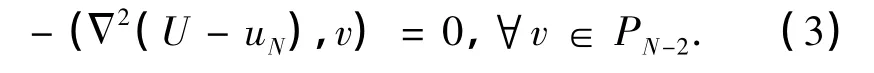
假设ω-1，-1U∈H2，设u*=ω1，1PN-22(ω-1，-1U)，e=uN-u*，有∶=ω-1，-1e∈N-2，因此，

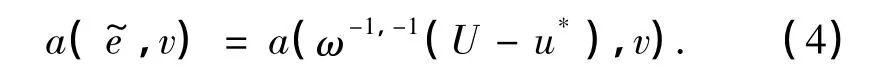
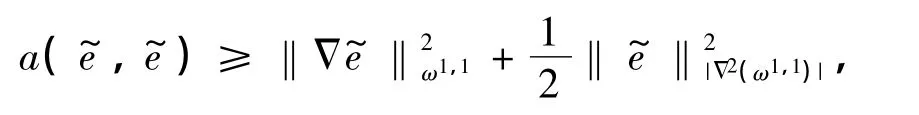
并且，

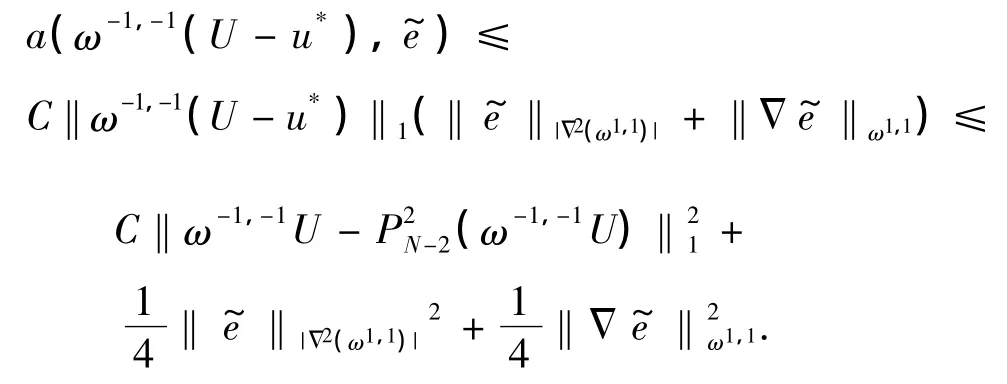
因此，由式(4)，得

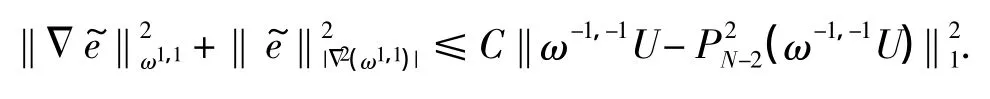
根据引理2，可得

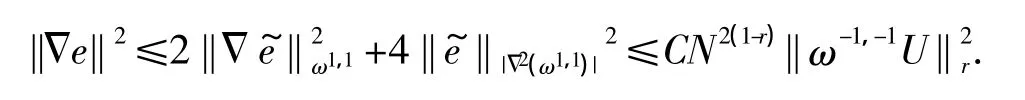
另一方面，

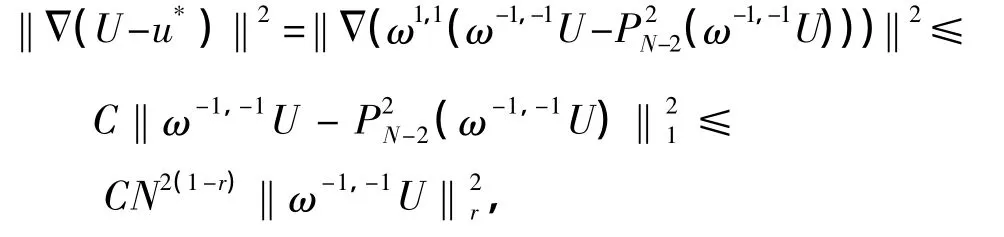
由三角不等式和Poincaré不等式，可以得到以下定理.

式中，C为依赖于‖ω-1，-1U‖r的正常数.

下面利用对偶技巧来估计‖U-uN‖.

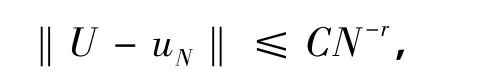
式中，C为依赖于‖ω-1，-1U‖r的正常数.

证明 考虑如下问题：对于g∈L2(Ω)，令φ= φ(g)，满足

根据文献［1］，可知式(5)有唯一解，并且φ满足

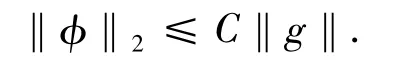
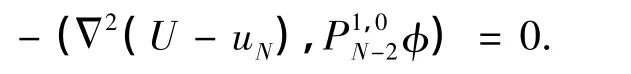
因此，

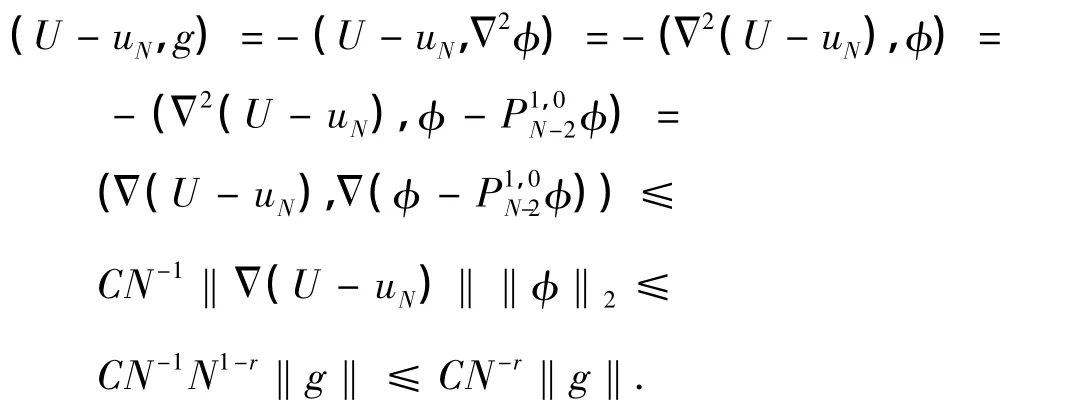
由定理1和定理2可知，条件ω-1，-1U∈Hr(Ω)稍严格，这里可以更仔细地考虑权的影响.如果采用适当的投影算子，例如考虑广义Jacobi投影算子，那么精确解可以属于较弱的带权Sobolev空间.

3 数值算例

例1 考虑如下二维 Poisson方程的齐次Dirichlet边值问题：

其精确解为

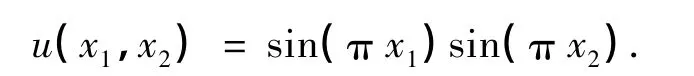
分别使用Legendre tau(LT)方法和Legendre Galerkin (LG)方法计算，得到的L2模误差如表1所示.

表1 例1的L2模误差Table 1 L2errors for Example 1

例2 考虑如下二维 Poisson方程的齐次Dirichlet边值问题：

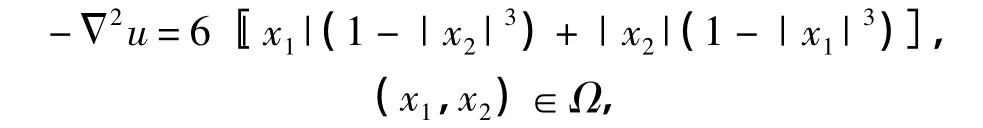
其精确解为

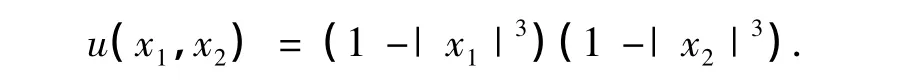
分别采用LT方法和LG方法计算，得到的L2模误差如表2所示.

由例2可以看出，因为解U∈H3.5-ϵ(Ω)(ϵ＞0)，所以其数值结果表明它能达到L2模下最优收敛阶，并且tau方法具有与Galerkin方法相似的收敛性态.

例3 考虑如下二维 Poisson方程的齐次Dirichlet边值问题：

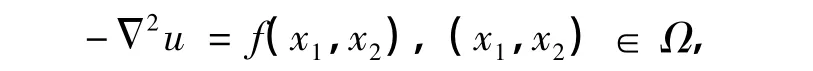
式中，

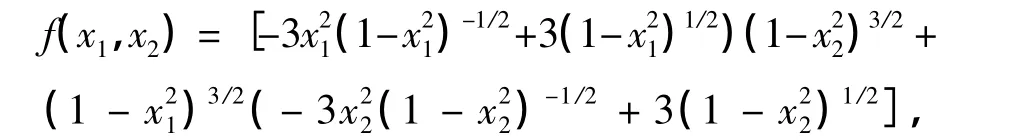
其精确解为

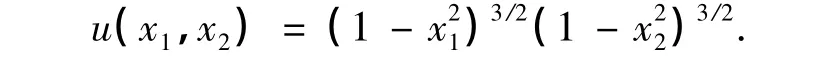
分别用LT方法和LG方法计算，得到的L2模误差如表3所示.

表2 例2的L2模误差Table 2 L2errors for Example 2

表3 例3的L2模误差Table 3 L2errors for Example 3

由例3可以看出，如果解在边界上有奇性，则LT方法的精度就不如LG方法.

例4 考虑如下二维 Poisson方程的齐次Dirichlet边值问题：

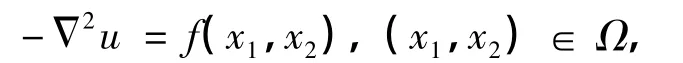
式中，

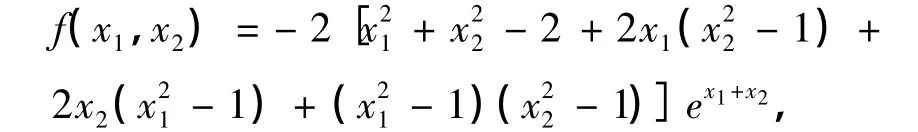
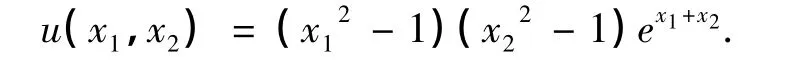
其精确解为分别用LT方法和LG方法进行计算，得到的L2模误差如表4所示.

表4 例4的L2模误差Table 4 L2errors for Example 4

通过上述算例，对于ω-1，-1U∈Hr(Ω)这个条件，当更仔细地考虑权的影响时，就可以看出LT方法与LG方法的区别，即如果解充分光滑或者解在区域内有奇性，则LT方法和LG方法几乎具有相同的精度;如果解在边界上有奇性，则LT方法的精度就不及LG方法.

［1］ BERNARDIC，MADAYY.Spectral methods，handbook of numerical analysis［M］.Amsterdam：Elsevier，1997：209-486.

［2］ CANUTOC，HUSSAINIM Y，QUARTESONIA，et al.Spectral Methods：fundamentals in single domains［M］.Berlin：Springer-Verlag，2006.

［3］ SHENJ，TANGT.Spectral and high-order methods with applications［M］.Beijing：Science Press，2006.

［4］ ALIABADIM H，ORTIZE L.Numerical treatment of moving and free boundary value problems with the tau method［J］.Comput Math Appl，1998，35(8)：53-61.

［5］ HOSSEINIS M，SHAHMORADS.Tau numerical solution of fredholm integro-differential equations with arbitrary polynomial bases［J］.Appl Math Model，2003，27：145-154.

［6］ SHENJ.A spectral-tau approximation for the Stokes and Navier-Stokes equations［J］.Math Model Num Anal，1988，22(4)：677-693.

［7］ TANGJ G，MAH P.Single and multi-interval Legendre tau-methods in time for parabolic equations［J］.Adv Comput Math，2002，17：349-367.

［8］ SHENJ.Efficient spectral-Galerkin method—(Ⅰ)direct solvers of second-and fourth-orderequationsusing Legendre polynomials［J］.SIAM J Sci Comput，1994，15(6)：1489-1505.

［9］ SHENJ.Efficient spectral-Galerkin method—(Ⅱ)direct solvers of second-and fourth-orderequationsusing Chebyshev polynomials［J］.SIAM J Sci Comput，1995，16(1)：74-87.

［10］ JUNS，KANGS，KWONY.A direct solver for the Legendre tau approximation forthe two-dimensional Poisson problem［J］.J Appl Math Comput，2007，23：25-42.

［11］ SACCHILANDRIANIG.Spectral tau approximation of the two-dimensional Stokes problem［J］.Numer Math，1988，52：683-699.

［12］ SHENT T，ZHANGZ Q，MAH P.Optimal error estimates of the Legendre Tau method for second-order differential equations［J］.J Sci Comput，2010，42(2)：198-215.