基于多输入多输出-正交频分复用系统的动态马尔可夫链蒙特卡罗检测算法

杨辉联， 杨建国， 石 海

(上海大学通信与信息工程学院，上海200072)

随着无线通信技术的发展，人们对4G通信系统的研究已经提上日程，其中最为关键的技术之一就是正交频分复用(orthogonal frequency division multiplexing，OFDM)［1-3］与多输入多输出(multiple input multiple output，MIMO)［4-6］相结合的 MIMOOFDM技术.该技术已被视为下一代高速无线通信网的核心技术，其主要特点就是可以有效地克服无线信道的频率选择性衰落，增加系统容量，以及提高频谱利用率.

近年来，许多学者致力于MIMO-OFDM系统中的多用户检测技术的研究［7-8］，并提出了一种基于马尔可夫链蒙特卡罗(Markov chain Monte Carlo，MCMC)方法的贝叶斯多用户检测算法［8］.该检测算法由系统状态构成马尔可夫链，并采用批处理的迭代思想和蒙特卡罗方法简化贝叶斯求解问题.在实际应用中，该算法不仅可以有效地抑制多径衰落、载波频偏以及相位噪声干扰，还具有较低的算法复杂度和高检测性能的特点.然而，该算法必须兼顾系统状态在各种干扰条件下的可能变化，因此，为了确保算法的检测性能，往往需要在设定一段迭代运算后，才可认为系统状态的采样值进入迭代收敛区间.故该算法不得不经过较长的迭代运算等待时间和一段有效的迭代运算之后，才能实现整个检测估计.由于采用较长的迭代运算等待时间，即使系统状态的样本收敛较快，算法的收敛速度仍无法得到改善，从而导致系统的实时性较差［9］.针对上述问题，本研究采用收敛阈值判决方法动态地监测系统状态的样本收敛状况，提出了针对MIMO-OFDM系统的动态MCMC贝叶斯多用户检测算法.该算法利用系统状态马尔可夫链前后样本的相关性与所设定的收敛阈值门限进行比较，动态地设定系统状态样本迭代收敛区间的起始时刻，以求进一步提高检测算法的实时性.

1 MIMO-OFDM系统模型

假设MIMO-OFDM系统的上行链路中有K个用户，其中第k个用户的发射机结构如图1所示.将发送端信息比特流编码成{bk}，编码比特再按有限字符集C={c1，c2，…，cM}映射调制成码元流{ak}，码元流{ak}经串/并变换成N个子码流ak，缓冲后得到NT个子码流，i=1，2，…，NT;再进行空时分组编码，编码后将数据流进行OFDM调制;最终，每个子码流经由其相应的NT个天线发送.因此，对于K个用户系统，发射端天线数为KNT，其中定义，且表示第k个用户在第i个发射天线上发送的数据，OFDM调制子载波间隔为为符号间隔.因此，当NT=2时，在相邻2个OFDM符号时隙内，用户k的传输矩阵就可以表示为

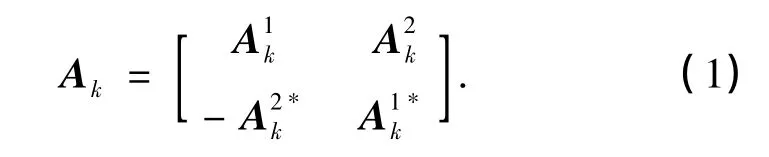
由图1可知，系统采用基于多个OFDM调制信号的空间复用技术，故对于每路发射天线发射的载波频段来说，仍将该系统视为平坦衰落的MIMO模型.假设用户k在第i个发射天线与第j个接收天线间的信道冲击响应为

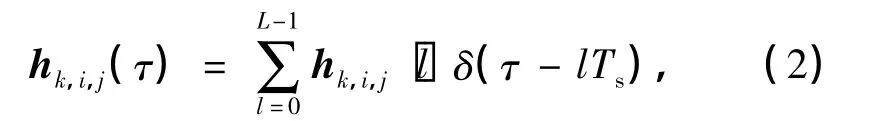
式中，L为多径传播的数目.在接收端，假设接收天线总数NR≥K，且接收信号经匹配滤波器、采样、去循环前缀以及离散傅里叶变换后，第j个接收天线在一个码元周期内的采样值所构成的接收信号的等效低通向量为rj=［rj［0］，rj［1］，…，rj［NTN-1］］T，j=1，2，…，NR，其表达式为

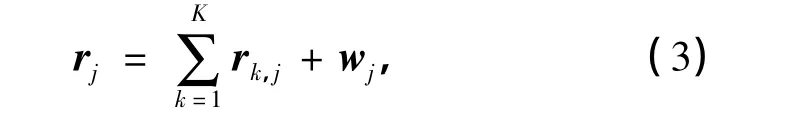
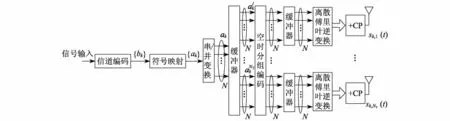
图1 第k个用户MIMO-OFDM系统上行链路的发送端框图Fig.1 Transmitter block diagram in the uplink of a MIMO-OFDM system with the k user

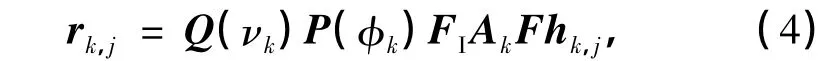
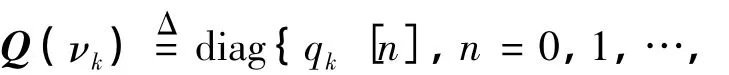
对于上述给出的第j个接收天线接收到的等效低通信号向量rj，本研究采用基于MCMC的贝叶斯多用户检测算法，并引入收敛阈值判决方法，构造针对MIMO-OFDM系统的动态MCMC贝叶斯多用户检测算法，以便在保持基于MCMC的贝叶斯多用户检测算法的性能的同时，降低检测算法的复杂度.

2 动态MCMC贝叶斯多用户检测算法

2.1 贝叶斯信号处理

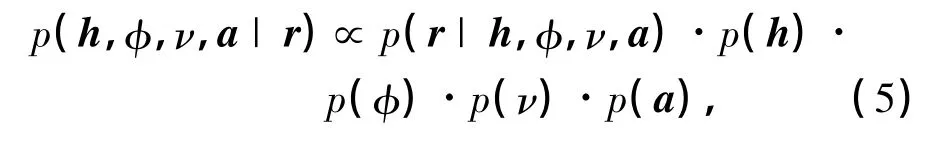
式中，

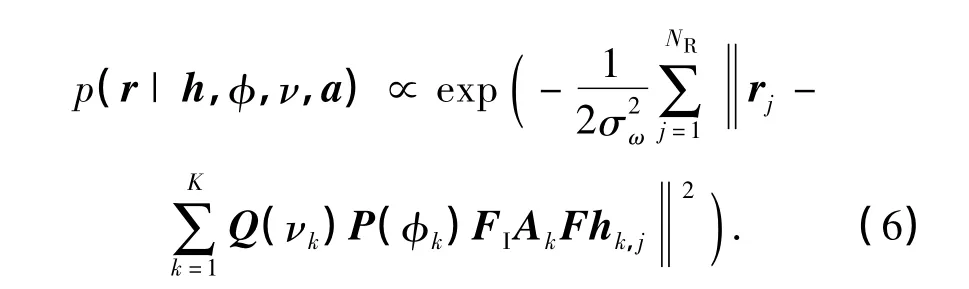
因此，发送符号ak［n］，k=0，1，…，K，n=0，1，…，N的贝叶斯检测可计算如下：

一种基于NB-IOT的智能垃圾桶设置有：单片机[1]；气味传感器[2]与单片机电连接，单片机与窄带物联网通信模块[3]电连接；窄带物联网通信模块通过无线信号与云端服务器连接，云端服务器通过无线信号与移动终端连接；太阳能电池板通过导线与蓄电池连接，蓄电池通过导线与单片机、红外传感器、空气质量检测器、异味传感器、窄带物联网通信模块电连接。

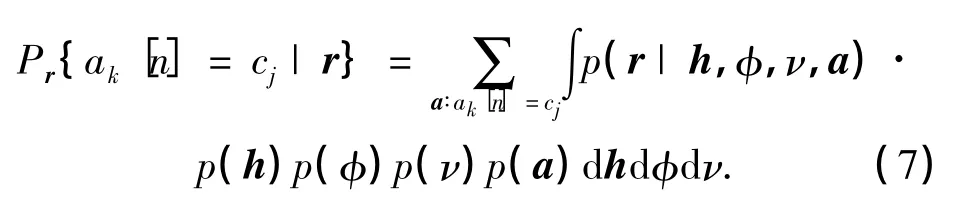
由式(7)可见，其计算涉及3KN-1重积分，故算法复杂度将随N呈指数增加，以至于在大多数实际应用场合下难以使用.为了降低式(7)的算法复杂度，目前常用蒙特卡罗方法来简化算法［3-6］.该方法对概率密度已知的随机变量，采用离散采样将积分运算简化为求和运算;对概率密度未知的随机变量，可寻求较容易获得的目标概率密度替代未知的概率密度，并通过迭代运算不断修正目标概率密度，以提高对未知概率密度函数估计的有效性.因此，蒙特卡罗方法不仅可以简便地描述随机变量的概率密度，还可以把复杂的积分运算简化成简单的求和运算.尤其是该算法所具有的迭代运算结构非常适合处理具有递归状态方程描述的通信系统，即若将式(7)中的(h，φ，ν)视为一个动态系统的变量，且满足马尔可夫链的状态方程，r为该动态系统的观测方程.则式(7)的多用户贝叶斯检测问题，就可以采用批处理的迭代思想和蒙特卡罗方法进行简化求解.由此，人们提出了MIMO-OFDM多用户通信系统的MCMC检测方法［7-9］.该方法不仅可以有效地克服多径衰落、载波频偏以及相位噪声的干扰，而且因批处理思想和蒙特卡罗方法的引入，使整个算法的复杂度得到了明显降低.

然而，在MCMC算法的求解过程中，由于系统的状态变量(h，φ，ν)具有随机变化的特性，因此，只有当系统状态处于动态平衡时，由蒙特卡罗方法获得的采样值及其概率分布才能确保系统的检测精度.但在实际应用中很难预知系统是否进入动态平衡状态，故一般需花费较长的等待时间才可认为系统进入动态平衡状态，然后在所设定的收敛区间内进行检测迭代估计运算，因而该算法的实时性较差.

2.2 动态MCMC检测算法

由上述分析可知，MCMC算法最大的弊端在于对系统状态动态平衡收敛区间起始时刻的选择.为了解决该问题，本研究采用监测系统状态变量马尔可夫链前后数据的相关性，并与设定的收敛阈值进行比较，以判定系统是否进入动态平衡状态，即对系统的状态变量(h，φ，ν)分别设定一个相应的收敛阈值.系统启动时即刻进入迭代运算，且在每次迭代运算后，计算每个状态变量的相关系数.当相关系数大于收敛阈值时，则认为系统状态进入动态平衡，然后再在收敛区间内进行最终的检测迭代估计运算，从而在确保估计精度的条件下，提高算法的实时性.基于式(7)，结合MCMC Gibbs采样方法［1］，本研究提出的MIMO-OFDM系统的动态MCMC多用户检测算法步骤如下：

(5)判断相关系数与门限是否满足关系

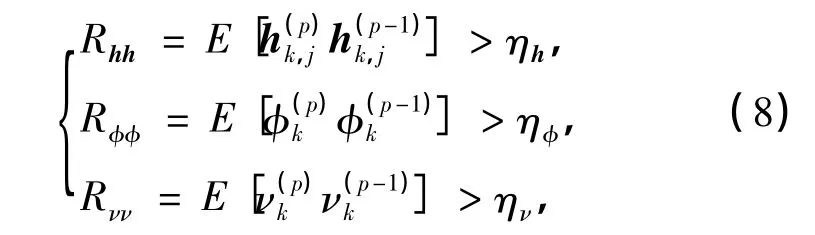
否则，重复步骤(2)～(4)的运算;

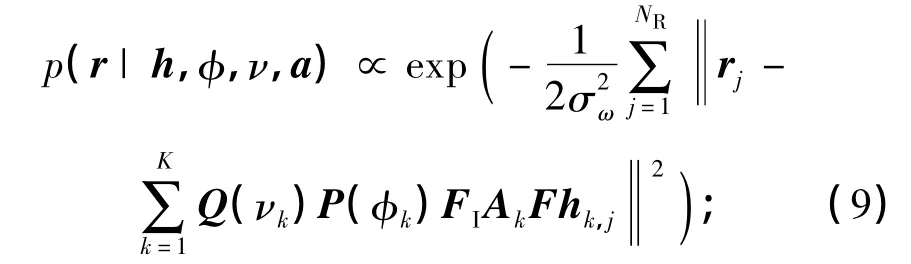
(7)对式(9)采样p0个样本，并由蒙特卡罗方法求解贝叶斯估计，即式(7)可简化为

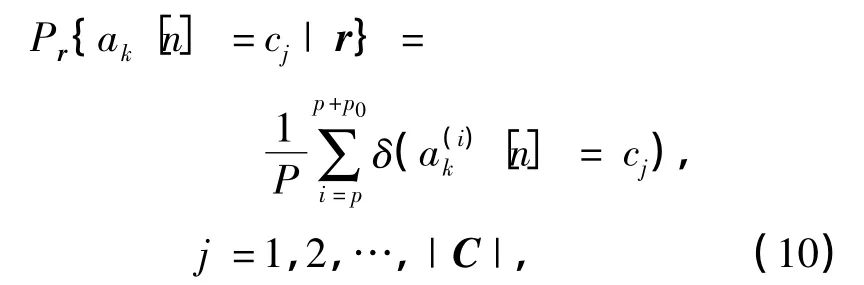
上述算法中，收敛阈值的取值为(0，1).该阈值的取值可以根据具体的实际应用情况来选定.选取的阈值越大，样本间的相关性就越大，从而检测估计的均值就越接近于无偏估计，而迭代运算次数则会增加，反之亦然.

3 仿真结果与分析

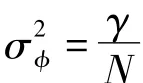
图2分别给出了现有的MIMO-OFDM系统多用户静态采样MCMC算法接收机与传统相关接收机的性能比较［8］.由图可见，在信道中存在频偏和相位噪声的情况下，采用现有的静态采样MCMC算法的接收机性能要明显优于传统相关接收机的性能.并且，随着采样迭代次数的增加，MCMC接收机的性能与理想信道(不存在频偏和相位噪声)下的相关接收机性能十分接近.

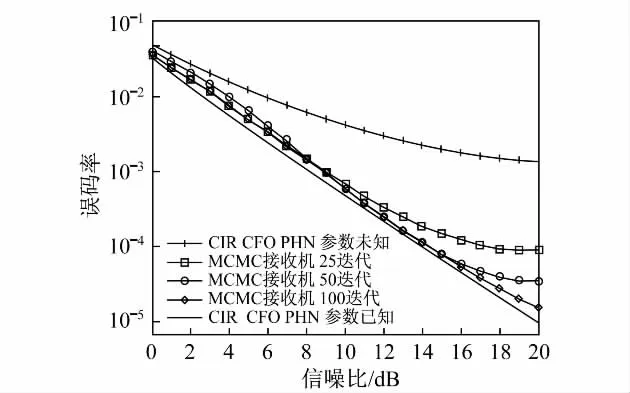
图2 MCMC接收机与相关接收机的性能比较Fig.2 Performance comparison with MCMC receiver and correlation receiver

图3分别给出了MIMO-OFDM系统MCMC接收机在迭代50次的情况下，原有的静态采样MCMC检测算法和本研究提出的动态采样MCMC检测算法的性能比较.由图可见，动态采样MCMC检测算法接收机的性能要优于静态采样MCMC检测算法接收机的性能，尤其在低信噪比时.这是因为在低信噪比的情况下，由于噪声干扰使得采样值与真实值误差较大，如果采用静态采样MCMC检测算法，将很难得到误差较小的样本值，从而无法实现精确的检测与估计;而采用动态采样MCMC检测算法，通过阈值判定选择样本值，只有当样本值之间的相关系数大于收敛阈值时，才会接受该样本值，从而在确保采样数据的可靠性前提下，提高检测估计的性能.

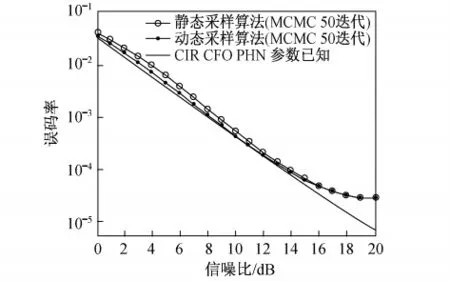
图3 MCMC接收机不同采样算法的性能比较Fig.3 Performance comparison with different sample algorithm in the MCMC receiver

图4给出了MCMC算法接收系统在信噪比为10 dB，频偏参量ν=-0.25的情况下，系统载波频偏状态样本值的收敛曲线.由图可见，MCMC迭代运算在大约40次迭代后，样本值总体上将收敛于频偏真实值，即系统已进入动态平衡状态.由此可见，此时动态MCMC算法即可进入迭代收敛区间进行检测估计运算，而静态MCMC算法则必须在所设定的第50次迭代后才可进入迭代收敛区间进行检测估计运算.值得注意的是，在收敛区间内样本值与真实值比较仍会出现较大的误差，其间，如果选用静态采样MCMC算法，将无法剔除误差较大的样本值，以致影响系统的检测性能.而采用动态采样MCMC算法，通过收敛阈值门限可筛选出可靠的样本值，以此确保系统的检测性能.可见，动态采样MCMC算法不仅可以提高算法的收敛速度，而且可以在很大程度上提高算法的估计精度.

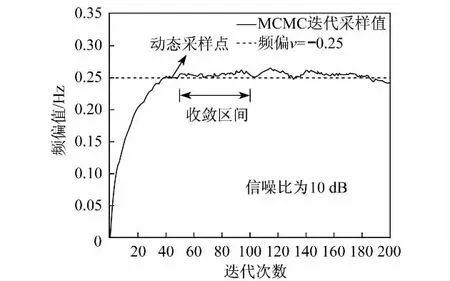
图4 频偏为0.25 Hz时，MCMC算法样本值的收敛曲线Fig.4 Convergence curveofMCMC algorithm in frequency offset 0.25 Hz

4 结束语

本研究针对4G系统中的马尔可夫链蒙特卡罗贝叶斯多用户检测算法作了一定的改进.仿真结果验证了改进算法的可行性，并证实了新的算法不论是在可靠性上，还是复杂度上都有着很好的性能.本研究所提出的思想不仅可用于今后4G系统中的MIMO-OFDM技术，也为目前TD-SCDMA的联合检测提供了一个可供参考的方法.

［1］ LIND D，PACHECOR A，LIMT J.Joint estimation of channel response，frequency offset，and phase noise in OFDM［J］.IEEE Transactions on Signal Processing，2006，54(9)：3542-3554.

［2］ MAN-ONP，MICHELEM，KUOC C J.Maximumlikelihood synchronization and channel estimation for OFDMA uplink transmissions［J］.IEEE Transactions on Communications，2006，54(4)：726-736.

［3］ YANGZ，WANGX D.A sequential Monte Carlo bind receiver for OFDM systems in frequency-selective fading channels［J］.IEEE Transactions on Signal Processing，2002，50(2)：271-280.

［4］ SUY T，ZHANGX D，ZHUX L.A low-complexity sequential Monte Carlo algorithm for blind detection in MIMO systems［J］.IEEE Transactions on Signal Processing，2006，54(7)：2485-2496.

［5］ LIANGP，LIP，FENGS P，et al.The low complexity deterministic SMC detection algorithm for MIMO system［C］∥ Proceedings of 2005 International Conference on Wireless Communications， Networking and Mobile Computing.2005：68-71.

［6］ GUOD，WANGX D.Blind detection in MIMO systems via sequential Monte Carlo［J］.IEEE J Sel Areas Commun，2003，21(3)：464-473.

［7］ PAPADIASC B，FOSCHINIG J.Capacity-approaching space-time codes for systems employing four transmitter antennas［J］.IEEE Transactions on Information Theory，2003，49(3)：726-733.

［8］ MERLIF Z，WANGX D，GIORGIOM V.A Bayesian multi-user detection algorithm for MIMO-OFDM systems affected by multipath fading，carrier frequency offset and phase noise［J］.IEEE J Sel Areas Commun，2008，26 (3)：506-516.

［9］ CHENR，LIUJ S，WANGX D.Convergence analyses and comparisons of Markov chain Monte Carlo algorithms in digital communications［J］.IEEE Transactions on Signal Processing，2002，50(2)：255-270.

［10］ PEARSONK.The history of statistics in the 17th and 18th centuries［M］.New York：Macmillan，1978：56-79.