Sine-Gordon方程的极限对称及应用

沈 青， 赵松林， 张大军

(上海大学理学院，上海200444)

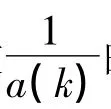
本研究将讨论sine-Gordon方程的一个新对称.该对称可以由已知的平方本征函数对称通过一个极限过程得到，而且由相应的对称约束得到的新解是一个二重极点解［7-9］，可以看作是方程的极限解.另外，平方本征函数与孤立子方程的自相容源之间有着紧密关系［10-11］.新的极限对称引出一个带新自相容源的sine-Gordon方程，本研究将利用双线性方法求解这个带源的方程.

1 Sine-Gordon方程的一个极限对称

Sine-Gordon方程为该方程最早来自于负常曲率曲面，可用于描述Josephson传输线中的磁通量子［12-13］、共振介质中的超短脉冲传播［14］等，具有丰富的物理与几何背景.Sine-Gordon方程是可积的，其Lax对为

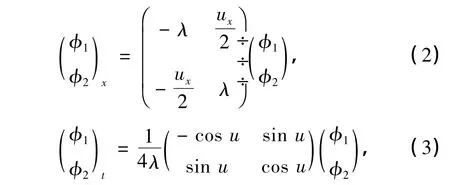
式中，λ为谱参数.可以验证，当φ1和φ2满足式(2)和(3)时，有

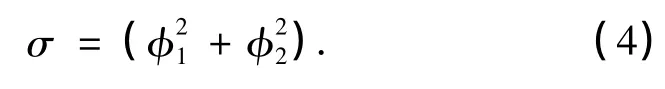
式(4)为sine-Gordon方程的一个对称，即满足σxt= σcos u.利用对称所满足的线性方程的线性性质，由式(4)以及方程的另一个对称ux，可以得到方程的一个对称约束为

式中，φij为Lax对当λ=λj时的解.由式(5)可以引出sine-Gordon方程的N-孤子解［15-16］.

引入

式中，φ1j和φ2j，ψ1j和ψ2j满足如下关系：

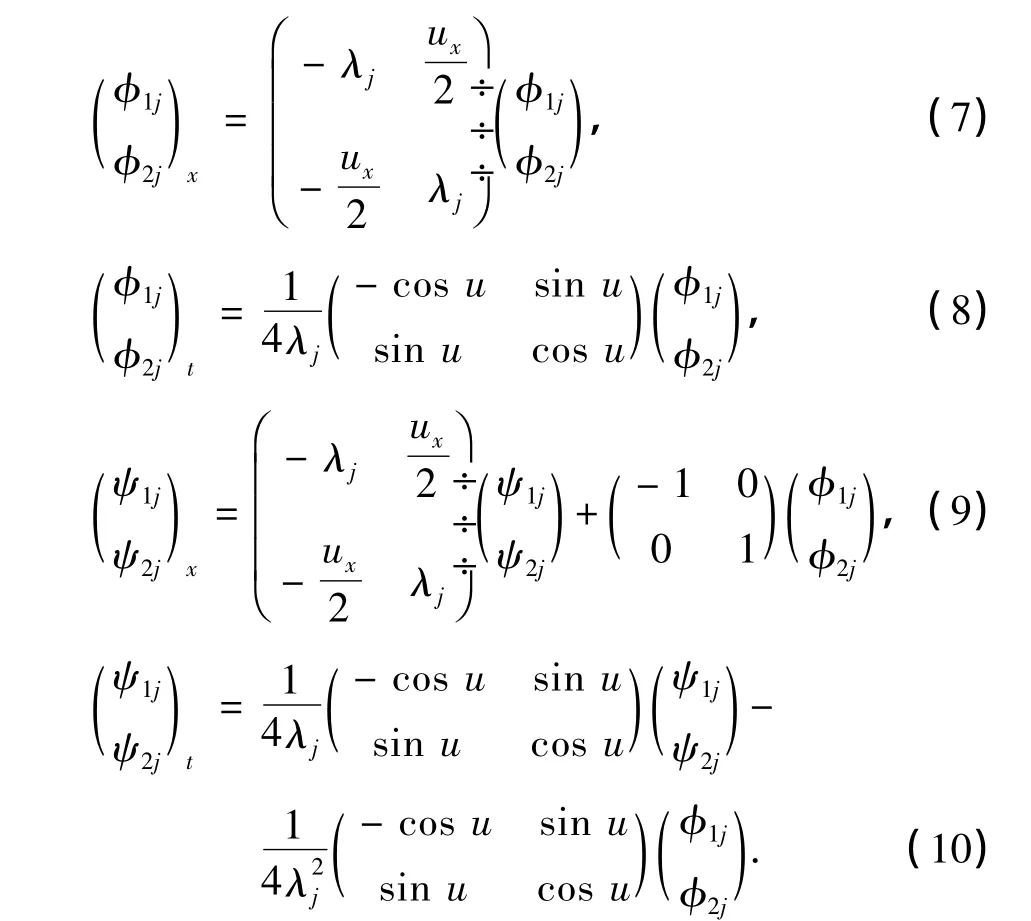
2 相似约化

2.1 相似约化与精确解

考虑式(1)的对称的组合

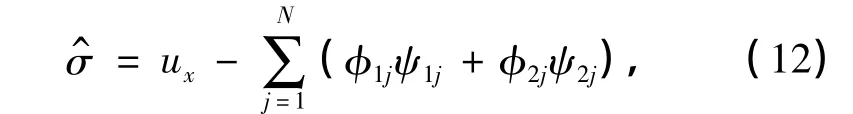
式中，φ1j，φ2j满足式(7)和(8)，ψ1j，ψ2j满足式(9)和(10).令σ^=0，有

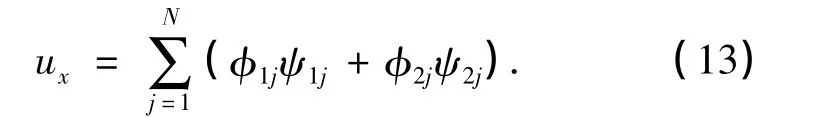
这是一个新对称约束.整个系统由式(1)，(7)～(10)，(13)组成，其中j=1，2，…，N.直接代入验证发现，当φkj，ψkj(k=1，2)满足式(7)～(10)时，由式(13)定义的u自动满足sine-Gordon方程.所以，此约束系统可以简化为

引入如下变换：

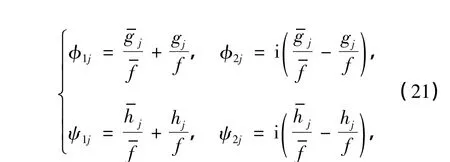
式中，i为虚数单位，“-”表示复共轭.将式(14)两边对x微分，利用式(20)和(21)，可以将式(14)～(19)写成如下双线性形式：

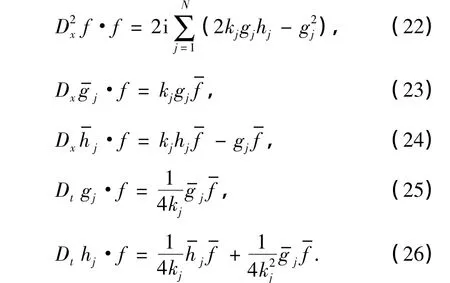
为了方便，在式(22)～(26)中已将λj记为-kj，算子 D即为所熟悉的 Hirota双线性算子［17］，定义为

为了精确地求解式(22)～(26)，将f，gj，hj分别按ε级数展开，有

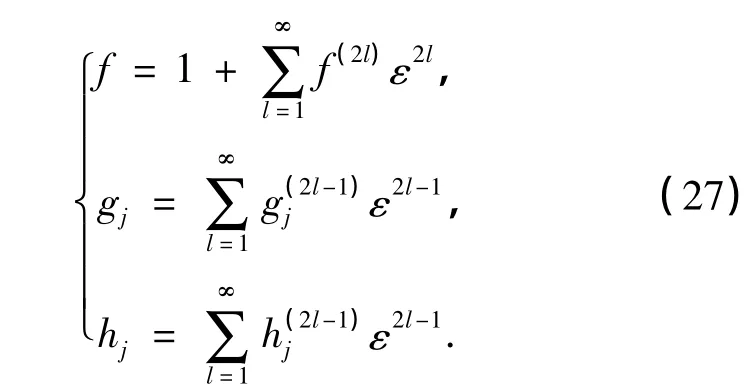
将式(27)代入式(22)～(26).当N=1时，经过计算发现，式(22)～(26)的解可以由截断的级数展开式(27)给出，其中

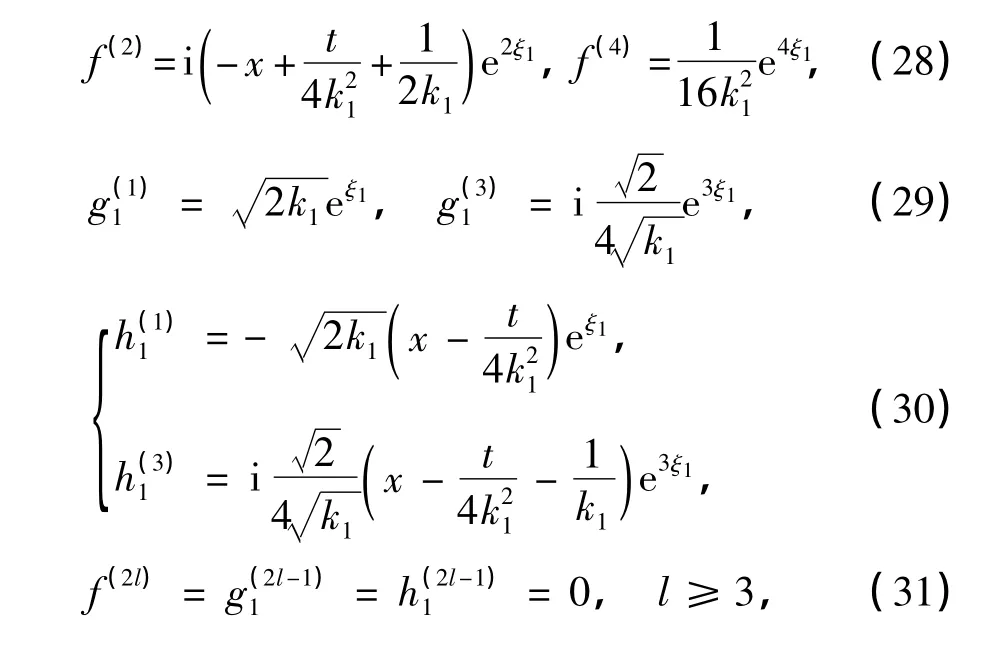
式中，k1，eξ(0)1都为实参数，且

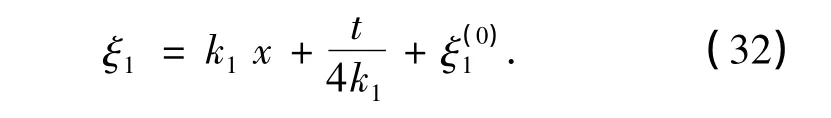
在式(27)中，取ε=1，由式(20)和(21)，可求得sine-Gordon方程的解为

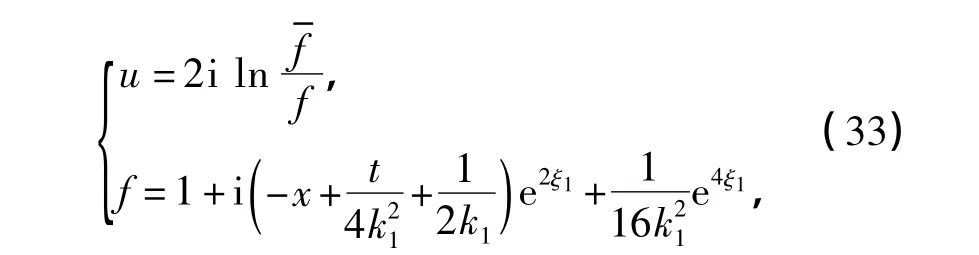
或表示为

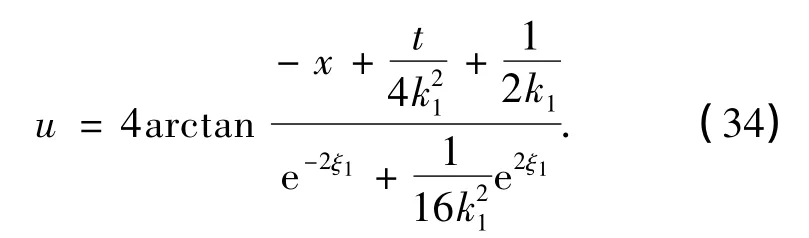
2.2 动力学分析

为了更好地分析式(34)的动力学特征，先来看sine-Gordon方程的2-孤子解，它可以写为［18-20］

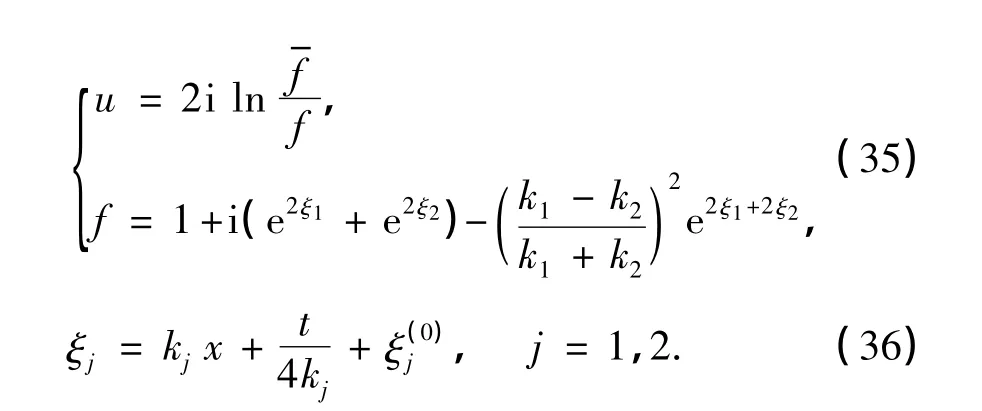
众所周知，sine-Gordon方程的单孤子解具有kink和反-kink两种类型，因此，2-孤子的相互作用也自然较KdV方程更丰富.

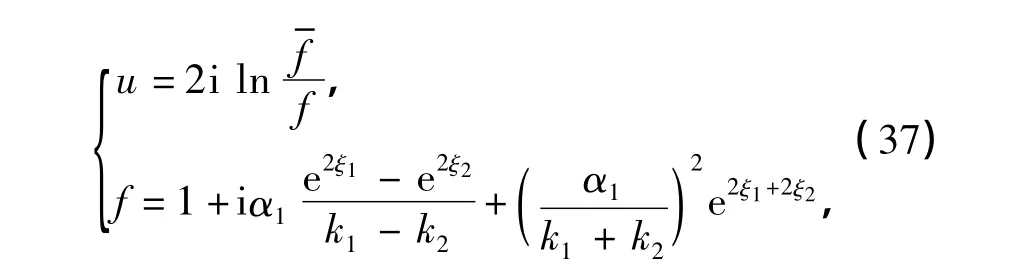
式中，

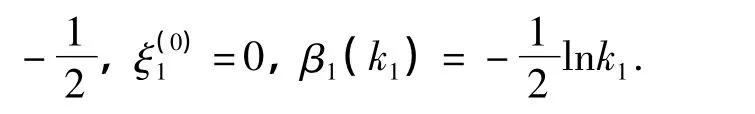
图1 Sine-Gordon方程的解(37)的图像Fig.1 Plots for solution of sine-Gordon equation given by(37)

在式(37)中，令k2→k1，并利用L’Hospital法则，可得

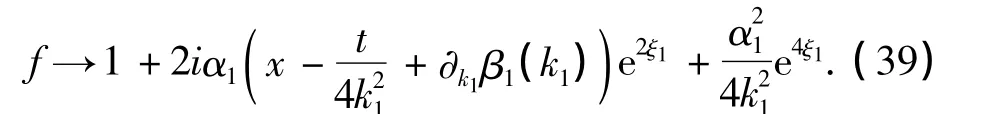
极限解(34)的图像如图2所示，其中k1=1，=0.

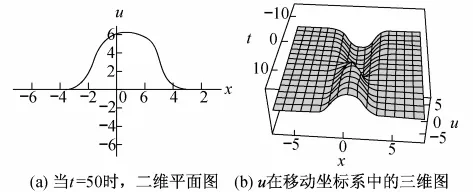
图2 Sine-Gordon方程的解(34)的图像Fig.2 Plots for solution of sine-Gordon equation given by(34)

显然，图2(a)中的波形是对称的，这正是2-孤子解(37)中k2→k1的体现.为了更好地研究解(33)的渐进性，将其放入如下移动坐标系内(见图2(b))：

通过渐进分析发现，图2(b)中4个拐点的轨迹可以用下述4条曲线来描述.

定理1 设式(34)中，k1＞0，则当t→-∞时，有2条移动的拐点轨迹，分别为

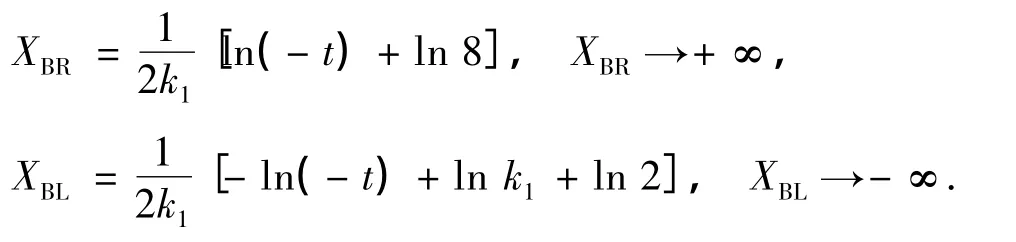
在拐点处，u的斜率分别为4k1和-4k1，u的值为u|XBR=u|XBL=-π.当t→ +∞时，有2条移动的拐点轨迹，分别为

在拐点处u的斜率分别为4k1和-4k1，u的值为u|XTL=u|XTR=π.

3 带新自相容源的sine-Gordon方程

在文献［21］中，带自相容源的sine-Gordon方程定义为

类似地，引入如下带极限源的sine-Gordon方程：

式中，{λj}互不相同，j=1，2，…，N.式(42)～ (44)为Lax可积系，Lax对为

式中，

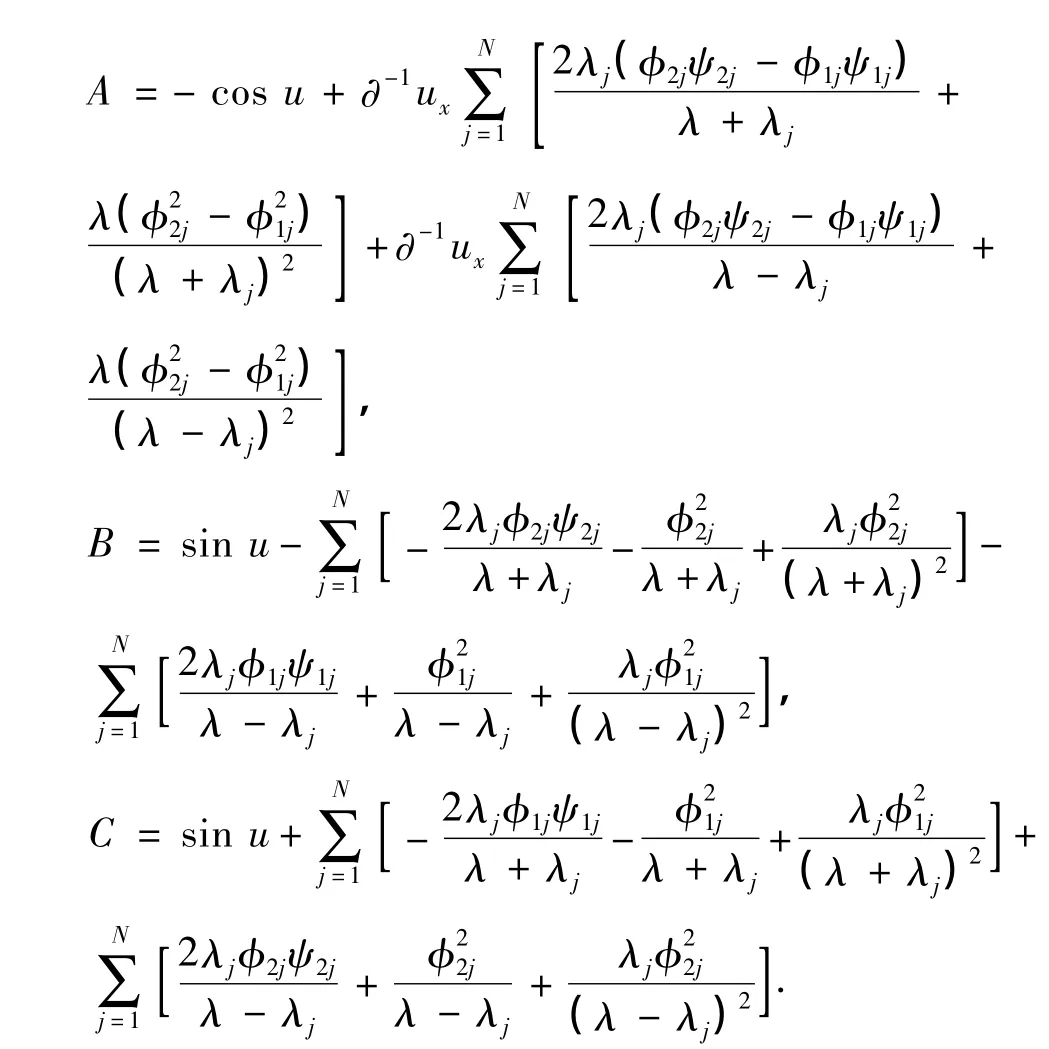
由式(45)的相容性条件，可导出式(42)，其中需利用如下关系：

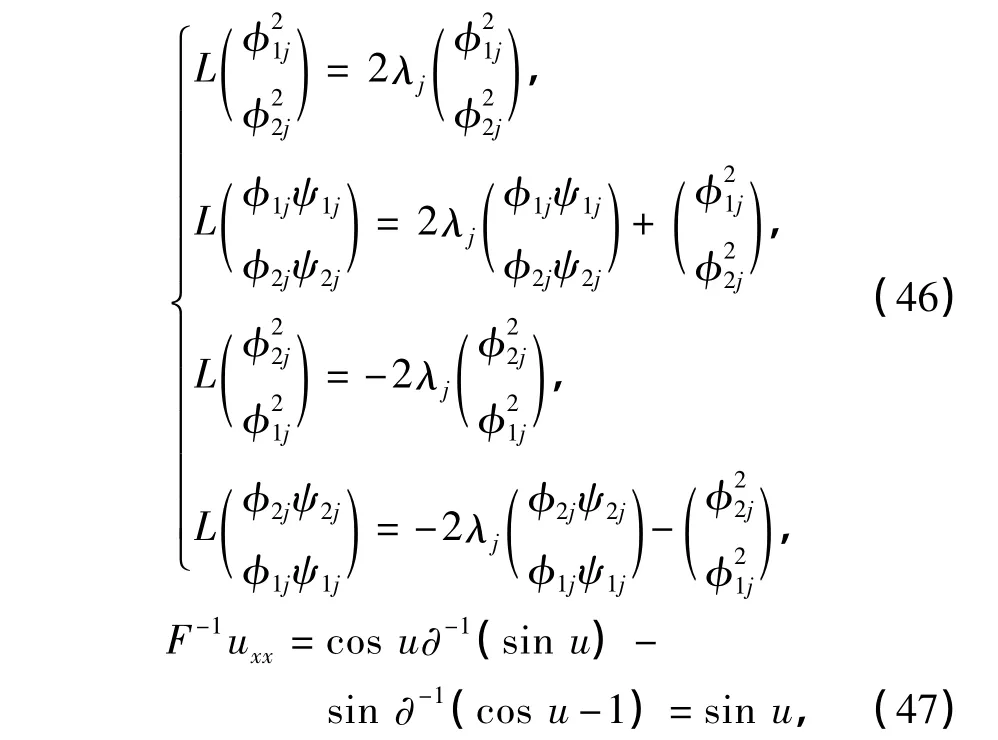
式(42)～(44)能够被精确求解.采用变换式(20)～(21)，则式(42)～(44)转化为如下双线性形式(λj=-kj)：

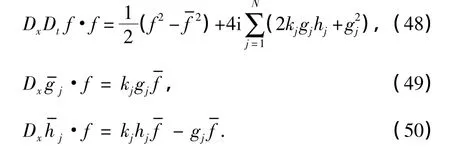
类似第2节中的求解过程，如式(27)，将f，gj，hj展开，并代人到式(48)～(50)中.当N=1时，可得

式中，

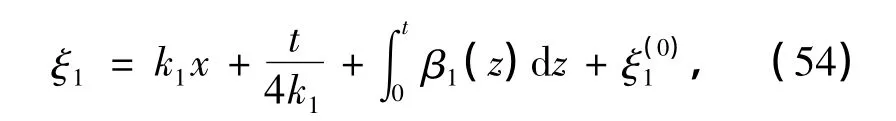
式中，k1，eξ(0)1为实参数，β1(z)为z的任意连续函数.在式(27)中，若取ε=1，可得式(42)～(44)的一个解为

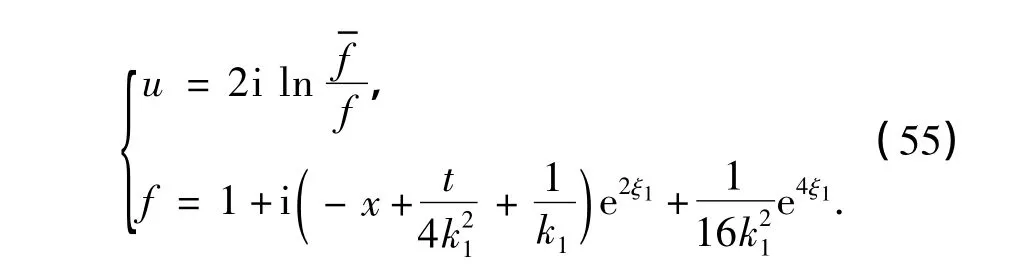
或写为

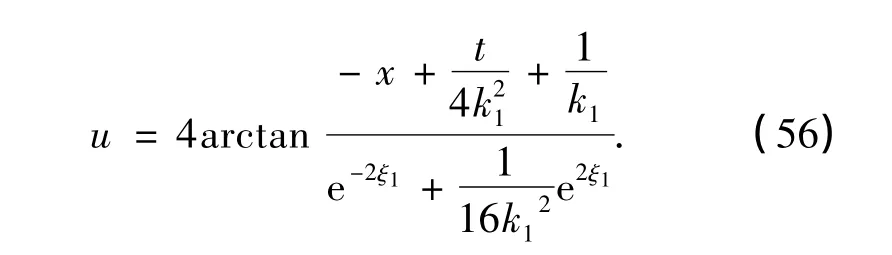
解(56)的图像如图3所示，其中k1=1，2，=0，β1(z)=3z2.

图3 带极限源的sine-Gordon方程的解(56)的图像Fig.3 Plots for the solution of sine-Gordon equation with new self-consistent sources given by(56)

4 结束语

本研究给出了与本征函数有关的sine-Gordon方程的新对称，这个对称与原有的平方本征函数对称之间存在极限关系，因此，称之为极限对称.由该对称引出的相似约化，可以得到sine-Gordon方程2-孤子解的极限解.本研究讨论了这个解与 sine-Gordon方程2-孤子解之间的极限关系，并分析了解的动力学特征.此外，本研究还利用极限对称给出了一个新的带源的sine-Gordon方程，该方程是Lax可积的，可以被双线性化，并且得到的解具有极限解的特征.本研究所讨论的极限对称与相应的方法可同样应用于其他可积方程.

［1］ OLVERP.Applications of lie groups to differential equations［M］.2nd ed.Berlin：Springer-Verlag，1993.

［2］ GARDNERC，GREENEJ，KRUSKALM，et al.Kortewegde Vries equation and generalizationsⅥ［J］.Comm Pure Appl Math，1974，27：97-133.

［3］ JIAOX，YAOR，LOUS Y.Approximate similarity reduction for singularly perturbed Boussinesq equation via symmetry perturbation and direct method［J］.J Math Phys，2008，49：093505.

［4］ 楼森岳，唐晓艳.非线性数学物理方法［M］.北京：科学出版社，2006.

［5］ JIAM，WANGJ Y，LOUS Y.Approximate symmetry reduction to the perturbed one-dimensional nonlinear schrodinger equation［J］.Chinese Physics Letters，2009，26：020201.

［6］ ZHANGD J，ZHANGJ B，SHENQ.A limit symmetry of the Korteweg-de Vries equation and its applications［J］.Theoretical and Mathematical Physics，2010，163：634-643.

［7］ WADATIM，OHKUMAK.Multiple-pole solutions of the modified Korteweg-de Vries equation［J］.J Phys Soc Jpn，1982，51：2029-2035.

［8］ CHEND Y，ZHANGD J，DENGS F.The novel multisoliton solutions of the mKdV-sine Gordon equations［J］.J Phys Soc Jpn，2002，71：658-659.

［9］ TAKAHASHIM，KONNOK.N double pole solution for the modified Korteweg-de Vries equation by the Hirota’s method［J］.J Phys Soc Jpn，1989，58：3505-3508.

［10］ ZENGY B，LIY S.The deduction oftheLax representation for constrained flows from the adjoint representation［J］.J Phys A：Math Gen，1993，26：273-278.

［11］ LINR L，ZENGY B，MAW X.Solving the KdV hierarchy with self-consistent sources by inverse scattering method［J］.Physica A，2001，291：287-298.

［12］ JOSEPHONB D.Supper current through barriers［J］.Advan Phys，1965，14：419-451.

［13］ REMOISSENETM.Wave called solitons，concepts and experiments［M］.2nd ed.Berlin：Springer-Verlag，1996.

［14］ LAMBG L.Analytical description of ultrashort optical pluse propagation in a resonant medium［J］.Rev Mod Phys，1971，43：99-124.

［15］ CAOC W.Nonlinearization of the Lax system for AKNS hierarchy［J］.Sci China，1990，33A：528-536.

［16］ CAOC W，GENG X G.Classical integrable systems generated through nonlinearization of eigenvalue problems［M］∥Nonlinear Physics，Research Reports in Physics.Berlin：Springer-Verlag，1990：68-78.

［17］ HIROTAR.Exact solution of the KdV equation for multiple collisions of solitons［J］.Phys Rev Lett，1971，27：1192-1194.

［18］ HIROTAR.Exact solution of the sine-Gordon equation for multiple collisions of solitons［J］.J Phys Soc Jpn，1972，33：1459-1463.

［19］ ABLOWITZM J，SEGURH.Solitons and the inverse scattering transform［M］.Philadelphia：SIAM，1981.

［20］ 陈登远.孤子引论［M］.北京：科学出版社，2006.

［21］ ZHANGD J.The N-soliton solutions of the sine-Gordon equation with self-consistent sources［J］.Physica A，2003，321：467-481.