最大距离可分码的上界

杨建生， 张运英， 王德秀

(1.上海大学理学院，上海200444;2.上海市亭新中学，上海201505)

设q，n，k为整数，且n≥k，A={0，1，2，…，q-1}(模q)为加法群.(n，qk，d)表示A上含有qk个码字且最小汉明距离为d的码.如果d=n-k+1，则称其为A上最大距离可分码，即MDS码.MDS码是组合数学研究的重要内容，Macwilliams等［1］认为：MDS码是编码理论中最令人着迷的一章内容.

MDS码一般分为线性和非线性.由于线性MDS码具有良好的代数结构与几何结构，因此，可以借助线性代数与有限几何的方法进行研究，其中特别引人注目的是“编码理论中的主猜想”的研究.

1 符号说明及MDS码的基本结果

设A为域，mq(k)表示A上的线性MDS码(n，qk，n-k+1)的最大码长，即mq(k)=max{n|存在A上(n，qk，n-k+1)MDS码}，则关于mq(k)的“编码理论主猜想”为

由于此猜想在编码理论与有限几何的研究中具有重要意义，因此，关于mq(k)的研究［2］十分丰富.

对于非线性MDS码，由于其缺乏良好的代数与几何结构，因此，很难找到系统的方法进行研究.从组合学角度考虑，非线性码的研究价值在于其应该具有比线性码更好的纠错能力.因此，对于非线性MDS码，研究人员提出了类似线性MDS码的问题，即在参数k确定的前提下，(n，qk，n-k+1)MDS码的最大码长Mq(k)具有什么性质?然而令人遗憾的是，研究Mq(k)的难度远大于研究mq(k).迄今为止，关于Mq(k)的研究［3-8］十分零散，并且主要采用有限几何的方法，其中有关Mq(k)的研究结果可概括为定理1和定理2.

定理1［7］(1)设k≥3，q＞2，如果存在(q+ k-1，qk，q)MDS码，则4整除q;

(2)设k＞3，q＞2，如果存在(q+k-1，qk，q) MDS码，则36整除q.

定理2［4］(1)对于(n，qk，d)MDS码，如果36不整除q，且k≥4，则n≤q+k-3;

(2)如果q＞2，且q≡2(mod 4)，则(q+1，q3，q-1)MDS码不存在.

由于MDS码缩短后仍为MDS码，因此，有如下引理：

引理1 Mq(k)≤Mq(k-1)+1.

本研究利用 MDS码的分割重量计数子(partition weight enumerator，PWE)和组合学方法研究Mq(k)，得到了Mq(k)一些新的上界.特别地，得到了Mq(q-1)≤q+1(q为奇数)，Mq(q-1)≤q+2 (q≡4(mod 6))，Mq(q-2)≤q+1(q≡4(mod 6))，Mq(k)≤q+k-3(q≡36(mod 180)，且k≥6).

为了讨论方便，下面引入一些符号和基本结果.

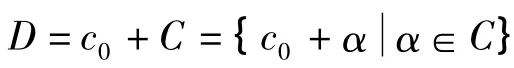
(3)对于A上的(n，qk，d)MDS码，其重量计数子［1］为

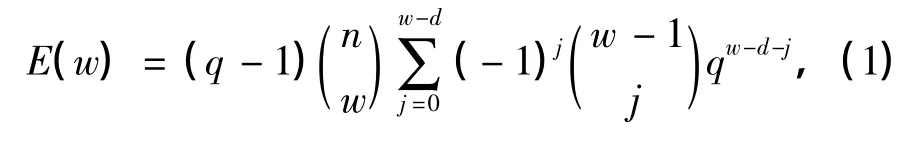
式中，w≥d.由文献［9］可知，式(1)不仅对线性的MDS码成立，对含有零码字的一般MDS码也成立.

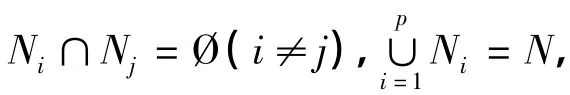
关于分割重量计数子，有如下定理成立.

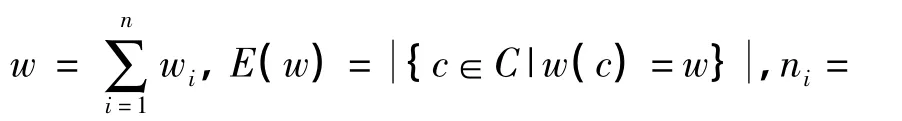
文献［10］在定理3的证明中假设A为域，但其证明与A是否为域无关，也与MDS码是否为线性码无关，只用到该MDS码含有零码字这个条件.因此，该定理对所有包含零码字的MDS码都成立.

2 MDS码新的上界

定理4 设q为奇数，则Mq(q-1)≤q+1.

证明 采用反证法.

假设C为一个包含零码字的(q+2，qq-1，4)(q为奇数)MDS码.考虑分割Γ=N1∪N2，其中N1= {1，2}.由定理3，得

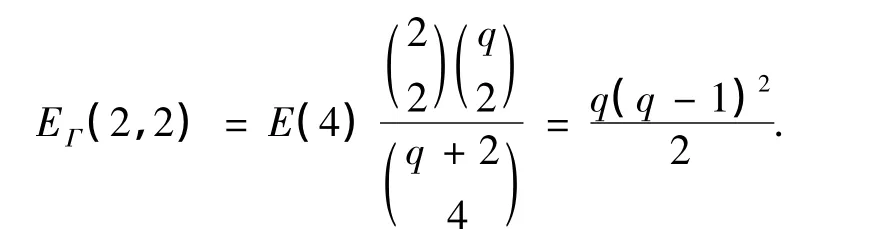
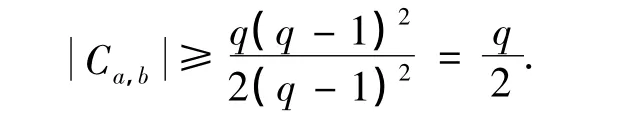
不失一般性，可以假设a=1，b=1.

设α，β∈C1，1，且α≠β.如果存在i∈Supp(α)∩Supp(β)，且 i≠1，2，则{1，2，i}⊂Supp(α)∩Supp(β).又因为w(α)=w(β)=4，则有d(α，β)≤3，矛盾.因此，Supp(α)∩Supp(β)={1，2}.

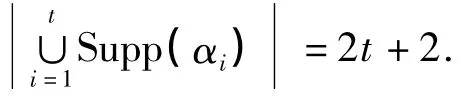
通过以上讨论，可得

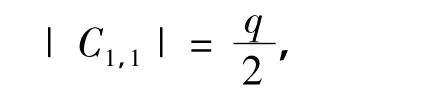
定理5 设k≥4，如果q是偶数，且(k-1)!不整除(q+k-4)…(q+1)q(q-2)，则Mq(k)≤q+ k-3，Mq(q-2)≤q+k-3.

证明 采用反证法.

假设C为一个包含零码字的(q+k-2，ql，d)(q为偶数)MDS码，其中l=k或者l=q-2，则

考虑分割Γ=N1∪N2，其中N1={1，2}.由定理3，可得

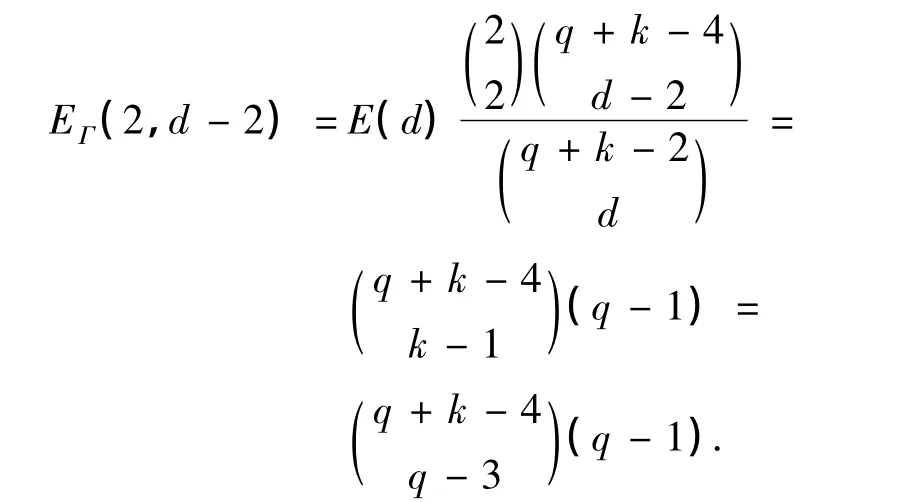
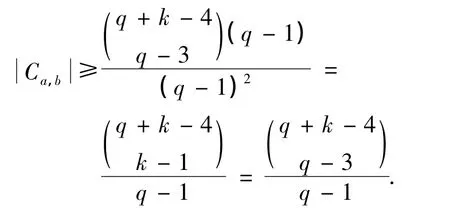
成立.

情况1 当l=k时.

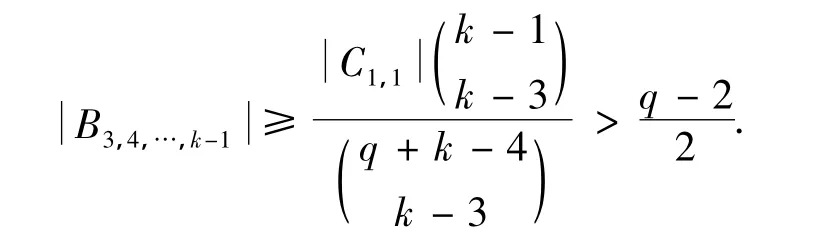
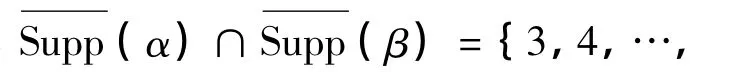
情况2 当l=q-2时.

令Bj1，j2，…，jk-3={α∈C1，1|ji∈Supp(α)，i=1，2，…，k-3}，其中j1，j2，…，jk-3为集合{3，4，…，q+ k-2}中k-3个不同的数.

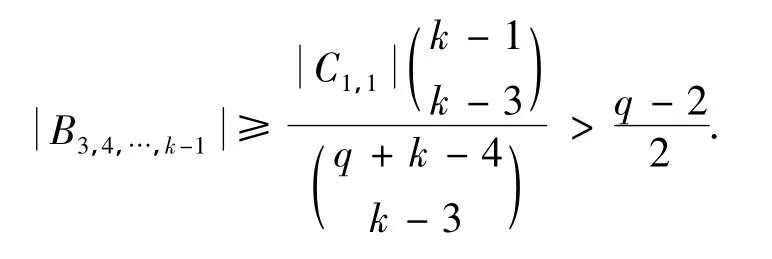
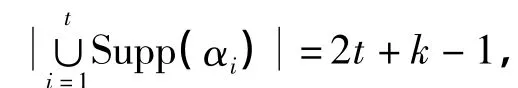
因此，当l=k或l=q-2时，有

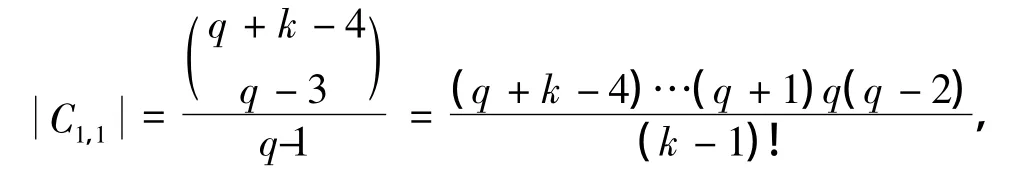
通过定理5，可以得到如下推论.

推论1 Mq(q-2)≤q+1(q≡4(mod 6)).

推论2 Mq(q-2)≤q+3(q≡6或26(mod 30)).

推论3 Mq(q-2)≤q+5(q≡8或36(mod 42)).

推论4 Mq(q-1)≤q+2(q≡4(mod 6)).

证明 由引理1，知Mq(k)≤Mq(k-1)+1.结合推论1，有Mq(q-1)≤Mq(q-2)+1=q+2(q≡4(mod 6)).

推论5 Mq(k)≤q+k-3(q≡36(mod 180)，且k≥6).

证明 如果k=6，由定理5知Mq(6)≤q+3 (q≡36(mod 180)).结合引理1，有Mq(k)≤q+k-3(q≡36(mod 180)，且k≥6).

［1］ MACWILLIAMSF J，SLOANEN J A.The theory of errorcorrecting codes［M］.Amsterdam：North-Holland Publishing Co，1977：317-329.

［2］ HIRSCHFELDJ W P.The main conjecture for MDS codes，lecture notes in computerscience［C］∥Proceedings of the 5th IMA Conference on Cryptography and Coding.1995：44-52.

［3］ ALDERSONT L.On MDS codes and Bruen-Silverman codes［D］.Ontario：University of Western Ontario，2002.

［4］ ALDERSONT L.Extending MDS codes［J］.Annals of Combinatorics，2005，9：125-135.

［5］ ALDERSONT L，BRUENA A.Codes from cubic curves and their extensions［J］.The Electronic Journal of Combinatorics，2008，15(1)：R42.

［6］ BRUCKR H，RYSERH J.The nonexistence of certain finite projective planes［J］.Canada J Math，1949(1)：88-93.

［7］ BRUENA A，SILVERMANR.On the nonexistence of certain MDS codes and projective planes［J］.Math Z，1983，183：171-175.

［8］ SILVERMAN R.A metrization forpower-setswith applications to combinatorial analysis［J］.Canad J Math，1960，12：58-176.

［9］ TOLHUIZENL M G M.On maximum distance separable codes over alphabets of arbitrary size［C］∥Proceedings of the 1994 IEEE International Symposium on Information Theory.1994：431.

［10］ EL-KHAMYM，MCELIECER J.The partition weight enumerator of MDS codes and its applications［C］∥Proceedings of the 2005 International Symposium on Information Theory.2005：926-930.