长为{4,5,6}的完备删位纠错码的存在性*

蒲利群，柴艳玲

(1. 郑州大学数学与统计学院，河南 郑州450001；2. 郑州城市职业学院，河南 郑州452370)

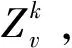
卫星通讯中，常常会出现信号衰减和数据丢失，删位纠错码为了解决此问题而产生。1992年Levenshtein[1]首次提出完备删位纠错码的概念，现已有大量文献对T(2,k,v)-码做了研究[2-6]，这些码中码字长度都是一个固定值。文[7]提出了具有混合长度的删位纠错码T(2,K,v)的概念，其中的码字长度取自一个给定的正整数集K；且对v≥3,v≠8，利用组合设计方法，在Zv上构造了具有混合长度{3,4,5}的T(2,{3,4,5},v)-码，并给出了码字总数的一个上界。本文研究K={4,5,6}时，T(2,{4,5,6},v)-码的存在性。

1 T(2,{4,5,6},v)-码的存在性

设K是给定的正整数集合，X是v个点的集合，B是k元有序组的集合,其中k∈K。若X的任意一个有序点对都恰好出现在B中的一个k元有序组中，则称(X,B)为一个有向成对平衡设计，简记DB(K,1;v)。其中，B中的任何一个k元有序组称为一个区组。

如果将DB(K,1;v)的所有区组看成码字，所有码字的集合就是一个T(2,K,v)-码。

在Zv上存在一个T(2,K,v)-码，等价于存在一个DB(K,1;v)。若K1⊆K2，T(2,K1,v)-码必为T(2,K2,v)-码。[8]利用组合方法构造，并给出了K={4,5}和K={5,6}时，DB({4,5},1;v)和DB({4,6},1;v)的存在性结论。

引理1[8]当v≥4,且v∉{6,8,9,12,14}时，DB({4,5},1;v)存在。

引理2[8]当v≡0,1 mod 3，v≥4，且v∉{9,15}时，DB({5,6},1;v)存在。

综合引理1和引理2，可以得到，当v≥4和可能的v∉8,9,14，存在一个T(2,{4,5,6},v)-码。于是，我们可以得到以下定理。

定理1 当v≥4，且v∉{8,9}和可能的v≠14时，存在一个T(2,{4,5,6},v)-码。

下面我们将在定理2和定理3中证明v∈{8,9}时，T(2,{4,5,6},v)-码不存在。

2 v∈{8,9}时，T(2,{4,5,6},v)-码的不存在性

设C是定义在Zv上的一个T(2,{4,5,6},v)-码，为叙述方便引入以下记号。

rj(x)：字符x在长为j的码字中出现的次数，∀x∈Zv；

bj：C中长度为j的码字个数。其中，j=4,5,6

引理3 设C是一个T(2,{4,5,6},v)-码，则有

(i)3r4(x)+4r5(x)+5r6(x)=2(v-1)，∀x∈Zv；

证明Zv中的任意点对都恰好出现在C的一个码字中，任意一点x与其他的(v-1)个点构成2(v-1)个序对。由于x出现在r4(x)个长为4的码字中，且每个码字都有3个含x的序对，因此，所有长为4的码字中共有3r4(x)个含x的序对。同理，所有长为5的码字中共有4r5(x)个含x的序对，所有长为6的码字中共有5r6(x)个含x的序对。从而，(i)式成立。

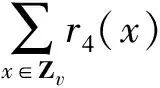
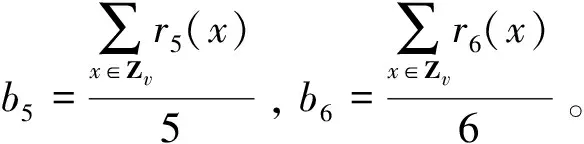
定理2 不存在T(2,{4,5,6},8)-码。

证明假设存在一个T(2,{4,5,6},8)-码C，由引理3得，

3r4(x)+4r5(x)+5r6(x)=14

于是，(r4(x),r5(x),r6(x))=(0,1,2)，(3,0,1)，或(2,2,0)。将Z8中的点划分成三类：

V1={x∈Z8|(r4(x),r5(x),r6(x))=(0,1,2)}，

V2={x∈Z8|(r4(x),r5(x),r6(x))=(3,0,1)}，

V3={x∈Z8|(r4(x),r5(x),r6(x))=(2,2,0)}

其中，|Vi|=vi，i=1,2,3。

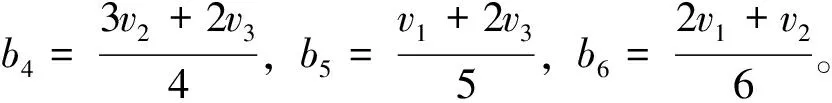
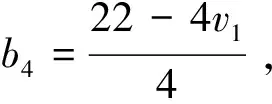
综上，不存在T(2,{4,5,6},8)-码。

定理3 不存在T(2,{4,5,6},9)-码。

证明假设存在一个T(2,{4,5,6},9)-码，由引理3得，

3r4(x)+4r5(x)+5r6(x)=16

于是，(r4(x),r5(x),r6(x))=(2,0,2)，(1,2,1)，(0,4,0)或(4,1,0)。将Z9中的点划分成四类：

V1={x∈Z9|(r4(x),r5(x),r6(x))=(2,0,2)}，

V2={x∈Z9|(r4(x),r5(x),r6(x))=(1,2,1)}，

V3={x∈Z9|(r4(x),r5(x),r6(x))=(0,4,0)}，

V4={x∈Z9|(r4(x),r5(x),r6(x))=(4,1,0)}

其中，|Vi|=vi，i=1,2,3,4。

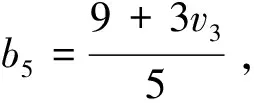
综上，不存在T(2,{4,5,6},9)-码。

3 码字总数的上界

4 小 结

本文证明了当v≥4时，v∉8,9和可能v≠14，T(2,{4,5,6},v)-码都存在，且给出了码字个数的一个上界。对v=14，如何构造出一个T(2,{4,5,6},14)-码，或者证明它不存在？

参考文献：

[1] LEVENSHTEIN V I. On perfect codes in deletion and insertion metric [J]. Discrete Math Appl, 1992, 2(3): 241-258.

[2] BOURS P A H. On the construction of perfect deletion-correcting codes using design theory [J]. Designs, Codes and Cryptography, 1995, 6(2): 5-20.

[3] MAHMOODI A. Existence of perfect 3-deletion-correcting codes [J]. Designs, Codes and Cryptography, 1998,14(1): 81-87.

[4] YIN J X. A combinatorial construction for perfect deletion-correcting codes[J]. Designs, Codes and Cryptography, 2001, 23(2): 99-110.

[5] SHALABY N, WANG J M, YIN J X. Existence of 4-deletion-correcting codes with length six [J]. Designs, Codes and Cryptography, 2002, 27(3): 145-156.

[6] WANG J M, YIN J X. Constructions for perfect 5-deletion-correcting codes of length 7 [J]. IEEE Transaction on Information Theory, 2006, 52(8): 3676-3685.

[7] 蒲利群, 柴艳玲. 长为{3,4,5}的完备删位纠错码的组合构造[J]. Journal of Mathematics, 2013, 33(1): 163-166.

[8] FUJI-HARA R, MIAO Y, WANG J M, et al. DirectedB(K,1;v) withK={4,5} and {5,6} related to deletion/insertion-correcting codes [J].Combinatorial Designs, 2001,9(12): 147-156.