如何正确运用方差分析——平衡不完全区组设计定量资料一元方差分析

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

平衡不完全区组设计是考察一个试验因素和一个区组因素对定量观测结果影响的一个试验设计方法，此设计方法是随机完全区组设计方法改良后的产物。本文将介绍该设计类型的要点、定量资料一元方差分析的模型和计算公式，以及基于SAS软件实现定量资料一元方差分析的方法。

1 平衡不完全区组设计的要点

在拟采用随机完全区组设计的试验研究场合中，若试验因素的水平数大于每个区组内可以容纳的受试对象（或观察单位）个数时，需要改用平衡不完全区组设计［1-2］。

平衡不完全区组设计的具体实施方法：基于定量观测指标，依据研究目的和专业知识，确定试验因素及其水平，并找出对定量观测指标影响最明显且来自受试对象的一个属性变量（也叫区组因素），将属性变量取值（即水平）相同的受试对象划分为一个大组；设试验因素有v个水平，区组因素有b个水平，每个区组内有k个受试对象，试验因素的每个水平重复出现r次。先从依据研究目的确定的具有同质性的总体中随机抽取b组受试对象，并要求下面两式成立：

在式（2）中，λ为每两种处理在不同区组中重复出现的次数。

【例1】用四种药物治疗脚气，6名受试者为两脚都患脚气的患者，每只脚接受一种药物治疗，观察指标为治疗效果评分（数值越大，疗效越好）。设计格式和资料见表 1［3］。

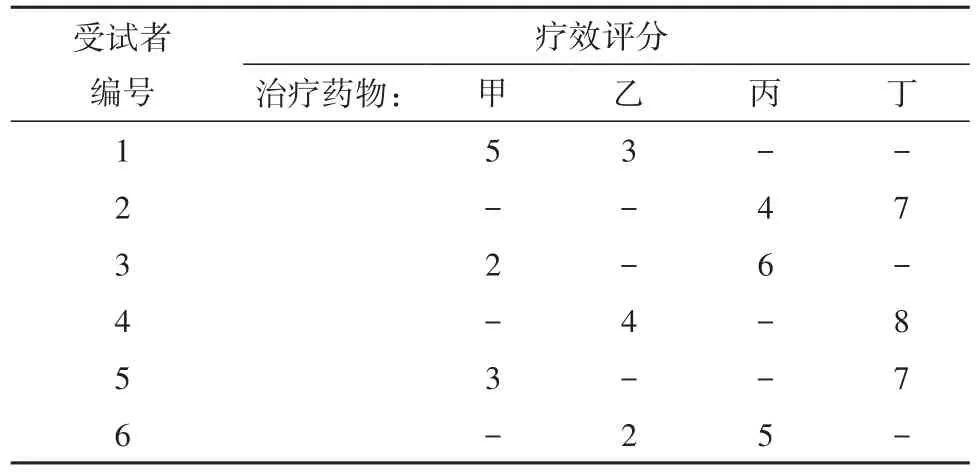
表1 四种药物治疗脚气的评分

【试验设计类型的辨析】本例中，v=4（药物有4种）、k=2（每位患者形成一个区组，每人有两只脚），r=3（每种药物被重复使用的次数），b=6（区组个数，即本例中的患者人数），满足rv=kb，即3×4=2×6；同时满足λ=r（k-1）/（v-1）=3（2-1）/（4-1）=1，λ为整数。故本例为平衡不完全区组设计。受试对象是6名患脚气的患者，试验因素是“治疗药物”，区组因素为每位患者（即个体差异），定量的观测指标为“疗效评分”。

2 平衡不完全区组设计定量资料一元方差分析

2.1 方差分析的模型

假定试验因素A与区组因素B之间的交互作用不存在或可以忽略不计。于是，它们之间各水平组合条件下可以不做重复试验；又假定试验因素A和区组因素B分别有v和b个水平。平衡不完全区组设计一元定量资料的方差分析模型［1］见式（3）：

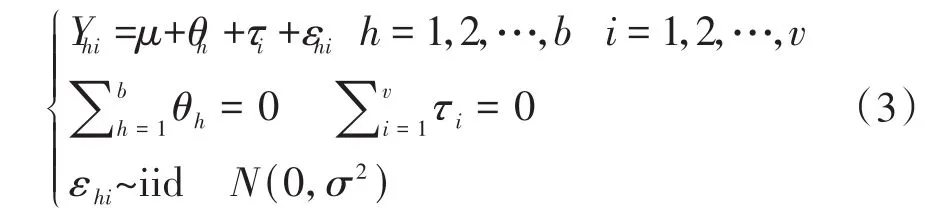
在式（3）中，Yij为两因素A、B的（i，j）水平组合下定量观测结果，μ为全部条件下定量观测结果的总体平均值，τi为试验因素A的第i个水平的效应，θh为区组因素B的第h个水平的效应。关于式（3）中各参数的最小二乘估计量，见文献［1］。

为检验一切μij是否相等，可改为检验以下两个假设。检验试验因素A的无效假设与备择假设分别见式（4）、式（5）。

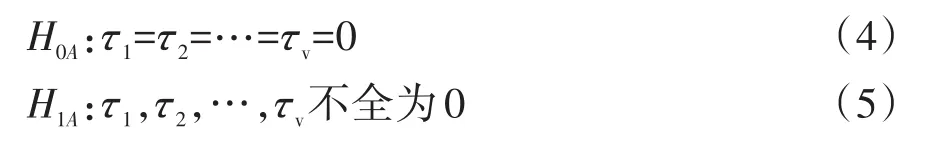
检验区组因素B的无效假设与备择假设分别见式（6）、式（7）。

2.2 方差分析的公式

平衡不完全区组设计定量资料方差分析公式见表 2［1］。

表2 平衡不完全区组设计两因素每种水平组合下进行一次试验的方差分析表

在表2中，5个离均差平方和以及FA的计算公式见下面各式：

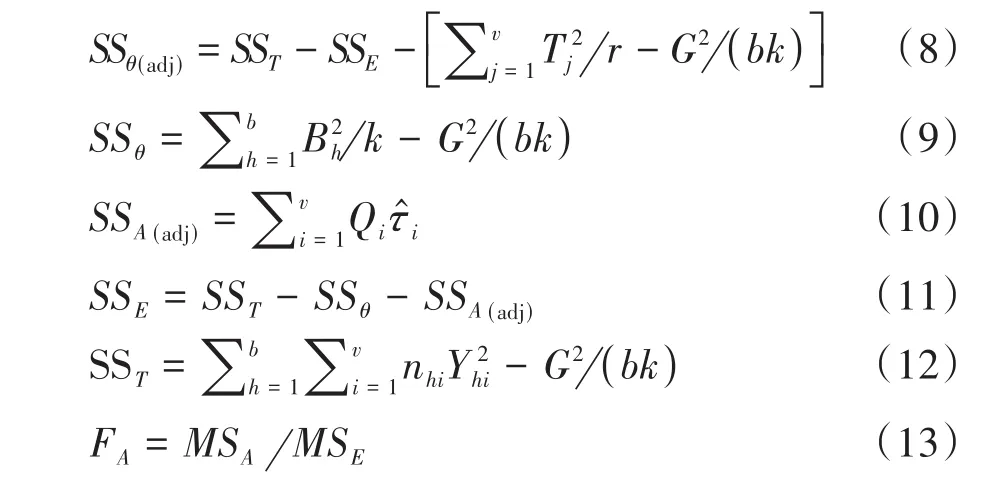
在上述各式中，有关符号的含义如下：

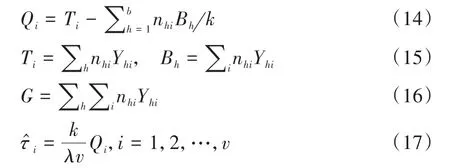
其中，Ti是第i个试验组中全部观测值之和，Bh是第h个区组中全部观测值之和，位于第h个区组且试验因素取第i个水平时，nhi=1，否则，nhi=0；G代表所有观测数据的总和。

3 平衡不完全区组设计一元定量资料的实例与SAS实现

3.1 实例与数据结构

【例2】某研究者为研究X线照射对血浆皮质酮的影响，以108只大白鼠为受试对象，将它们按性别、体重等分成12个区组，每个区组内的9只大白鼠性别相同且体重最接近，它们被随机均分成3个试验单位，每个试验单位包含3只大白鼠。设一个对照组，记为a；另设8个试验组，分别记为b、c、d、e、f、g、h、i。总共9种处理，每种处理重复4次。给予试验组中每只大白鼠500 R X线照射，对照组大白鼠不接受照射。试验因素为照射后观测结果的时间，对照组大白鼠的观测时间为0，而8个试验组的观测时间分别为1、5、12小时及1、3、7、10、14天，在这8个时间点取血样测定。每个观测时间点上观测每个区组中的一个试验单位（即3只大白鼠），观测结果变量Y为每个试验单位3只大白鼠皮质酮含量（μg/100 mL）（简称“含量”）之和。数据格式见表 3［4］。

表3 大白鼠受500 R X照射后不同时间的血浆皮质酮含量（μg/100 mL）

【试验设计类型的辨析】因v=9（试验因素的水平数），b=12（区组因素的水平数），k=3（每个区组内能容纳的受试对象数，本例中为试验单位数），r=4（每种处理重复次数），满足以下两个关系式：rv=kb=4×9=3×12=36；λ=r（k-1）/（v-1）=4（3-1）/（9-1）=8/8=1（λ必须为整数，代表每两种处理同时出现的区组个数）。

由此可知，本例的试验设计类型为“平衡不完全区组设计”。

3.2 用SAS实现方差分析

3.2.1 对例1的分析与解答

【分析与解答】设例1资料所需要的SAS程序如下：

【SAS输出结果及解释】

以上第一部分是关于总模型的方差分析结果，总模型具有统计学意义（F=21.96，P=0.013 9）。

以上第二部分结果表明：治疗方法（treat）对定量观测指标的影响有统计学意义（F=17.67，P=0.020 7），说明不同治疗方法的疗效是不同的；受试者（block）对定量观测指标的影响无统计学意义（F=6.87，P=0.071 8），说明不同患者的疗效之间的差别不明显。

由图1可看出：方法d的疗效最好，它与其他三种方法的疗效差异均有统计学意义（P均＜0.05）；方法c的疗效优于方法b，差异有统计学意义（P＜0.05）；方法a与方法b的疗效差异无统计学意义，方法a与方法c的疗效差异无统计学意义（P均＞0.05）。

图1 基于TUKEY法对4个均值进行两两比较的结果（平衡不完全区组设计）

值得一提的是，由于受试者对结果的影响没有统计学意义，故可以采用单因素4水平设计定量资料一元方差分析处理该定量资料。其对应的SAS过程步程序如下：

【SAS输出结果及解释】

以上结果表明：治疗方法（treat）对定量观测指标的影响具有统计学意义（F=10.10，P=0.004 3），说明不同治疗方法的疗效是不同的。

由图2可以看出：方法d与方法a和方法b的疗效差异均有统计学意义（P均＜0.05）；但方法d与方法c的疗效差异无统计学意义。相对来说，方法d的疗效比较好，方法c的疗效尚可，方法b和方法a的疗效最差。

图2 基于TUKEY法对4个均值进行两两比较的结果（单因素4水平设计）

3.2.2 对例2的分析与解答

【分析与解答】设例2资料所需要SAS程序如下：

【SAS输出结果及解释】

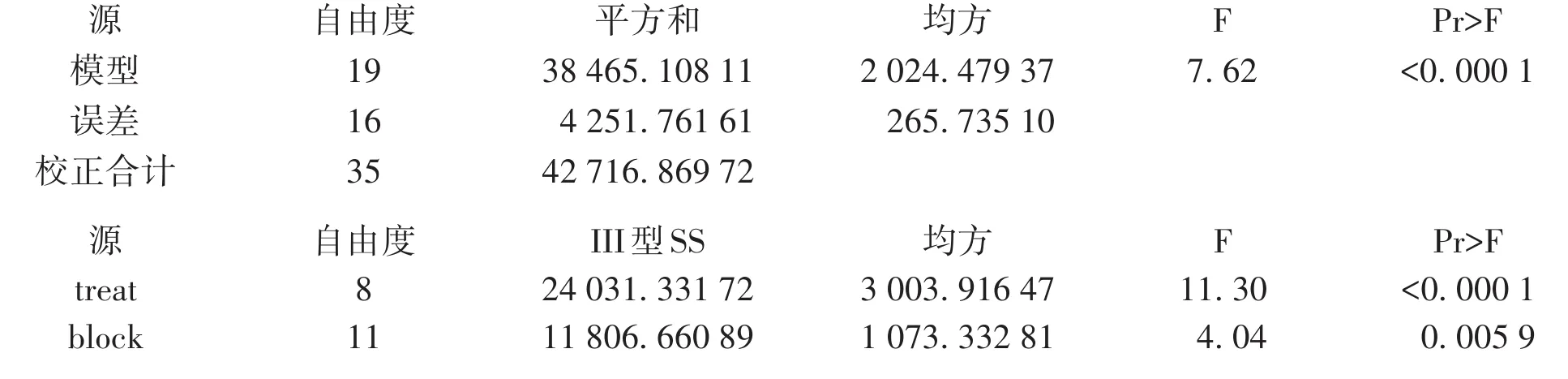
以上第一部分是关于总模型的方差分析结果，总模型具有统计学意义（F=7.62，P＜0.000 1）。

以上第二部分结果表明：试验因素（treat）和区组因素（block）对定量观测指标的影响均有统计学意义，对应的F值和P值分别为：试验因素（F=11.30，P＜0.000 1）、区组因素（F=4.04，P=0.005 9），说明考虑并设置了区组因素是有价值的。

从图3可看出，b、c、d三组的均值比较大，而其他六组的均值较接近。

图3 9个处理组观测结果变量的箱图

大白鼠接受500 R X线照射，血浆皮质酮含量均值迅速上升，从未照射时的63.950（对照组a）迅速上升到照射后1小时的117.950（试验组b），进而继续攀升到照射后5小时的128.800（试验组c），在此后的一段时间内是否继续上升不得而知（因为没有设置观测点），但到照射后12小时，均值已下降到105.525，随后缓慢下降并趋于平稳状态，到照射后第10天、14天，均值分别为51.025和51.725。

4 讨论与小结

4.1 讨论

分别采用平衡不完全区组设计和单因素4水平设计定量资料一元方差分析处理例1中的定量资料，得到的结果略有差别，这是由于设计类型的改变直接导致模型误差均方的改变。误差均方可能变大也可能变小，但误差项的自由度肯定会增大，这也就意味着计算结果的稳定性增大了。一般来说，当发现一个多因素设计定量资料一元方差分析的结果中存在多项无统计学意义的项时，从方差分析的模型中删除它们，本质上就是将它们的离均差平方和与原先模型的误差项的离均差平方和进行合并。当然，它们所对应的自由度也应与原先模型误差项的自由度进行合并。因此，合并后误差均方与原先模型的误差均方相比较，其数值可能变大也可能变小，但从理论上来讲，由于误差项的自由度增大了，合并后的方差分析模型与定量资料的吻合程度更高，结果更稳定，结论更可信。

从试验设计角度考量，本文例2在试验设计上可能存在值得商榷之处。因为处理因素有9个水平，而每个区组内也正好有9只大白鼠。这表明，每个区组内所能容纳的受试者数目恰好等于处理因素的水平数，可以采用“随机完全区组设计”，而没有必要选择“平衡不完全区组设计”。因为后者与前者相比，不仅增添了试验设计上的复杂度，而且统计分析也更复杂（特别是在缺乏统计软件的条件下），还可能降低结果的精确度（因为是不完全区组）。只有在客观条件（如例1）不允许的情况下，才考虑采用平衡不完全区组设计。

4.2 小结

本文介绍了平衡不完全区组设计的要点，介绍了该设计定量资料一元方差分析的模型和方差分析公式，基于SAS软件对两个实例进行了详细分析，并对多个均值进行了两种类型的多重比较，即两两比较和各试验组均值分别与同一个对照组均值之间的比较［5-6］。在讨论中，还阐释了随机完全区组设计与平衡不完全区组设计之间的异同点。