小学数学教学应引领学生深度思考

文|兰荣富

一、提供亲身体验，让思考更有根

小学数学教学中，建构体验学习模式，学生能更好地从现象看到事物的本质，增强教学效果，达到深度理解的学习目标。

如，教学《长方体的认识》，组织学生小组内动手操作，讨论交流哪一号的材料可以搭出长方体框架？

?

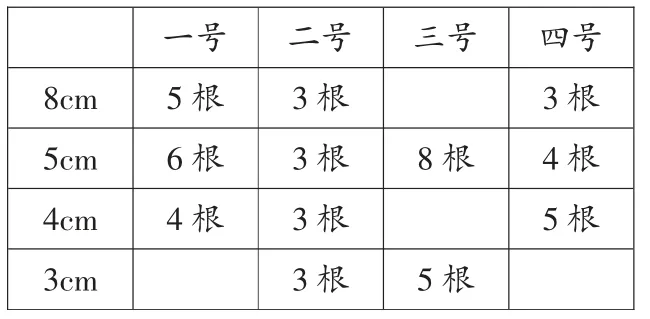
小组成员之间相互探讨，不断尝试，在动手操作中亲自感受不同长度小棒的组合，在实验、分析、思考中发现：三组不同长度的小棒，每一组至少要有4根；两组不同长度的小棒，有一组至少要有8根小棒，另一组至少要有4根。学生不再是被动接受知识，而是深度参与，积极体验，真正实现“自我发现的东西能积极地同化，从而产生深刻地理解”。不仅深化了对长方体棱特征的认知，也促进了学生数学思维能力的提升。

二、借助直观演示，让思考更有据

小学生思维以具体形象思维为主。教学中应该有目的地组织学生观察、比较，启发学生发现问题，引发学生数学思考。

如，教学一年级加减混合时，教师用课件动态演示天鹅飞行的过程：先在屏幕上出现湖里有4只天鹅，又飞来3只天鹅的场面。接着出现声音：你能从屏幕上提出一个数学问题吗？生：湖里一共有几只天鹅？紧接着追问：要算湖里一共有几只天鹅应该怎样列式？学生争先恐后回答：4+3。下一步接着在屏幕上出现原先湖里的7只天鹅飞走2只的场面。师：湖里天鹅的只数发生了什么变化，现在还有几只天鹅？教师配合学生的回答在“4+3”的后面写“-2”，把算式写完整4+3-2=5（只）。这样，学生在观察天鹅飞行的过程中，凭借直观演示过程，深刻体会到4+3-2=5的加减混合运算的意义，经历加减混合计算的过程。像这样通过生动形象的动画演示，让学生有思考的依据，在兴奋与激动中不知不觉地理解计算的过程。

三、借助动手操作，让思考更有序

在动手操作时，让学生应用数学语言有条不紊地表述操作过程，叙述自己思考的过程，把动手操作、动口表达和动脑思考三者有机地结合在一起，这样更能促使学生将感性的知识转化为抽象的思维，提高其思考能力。

如在教学《三角形内角和》一课时，教师需要让学生掌握三角形内角和是180度的知识点。除了常用的撕纸拼接法，教师还可以让学生运用三角尺，三人一组进行合作，每个人找出自己的直角三角尺、等腰三角尺，采用不同的方法进行拼接，再用量角器测量每一种拼接方法的角，无论怎样拼接，学生最终都会得到“三角形内角和为180度”的结论。此外，学生在探究时投入到实际动手操作中，可以对三角形这一图形性质的理解与掌握更加深入，便于学生运用三角形这一性质解决实际数学问题。

四、组织互动交流，让思考更宽广

课堂上，当教师提出一个问题之后，不要急于给出结果或进行评价，要留给学生足够的思考时间，让学生先在小组内进行交流，再进行汇报，互相倾听，互相启发，充分展示自己的思维过程，从而实现知识的自主建构。

如在教学一年级《百数图》一课时，先让学生认识教材中已知四支数字队伍的特点，再让学生补充百数图中剩下的数，接着引导学生进行观察、比较，发现了什么？这时让学生思考，先与同桌交流，再指名汇报：

生1：横着看，依次加1；竖着看，依次加10。

生2：我有补充，横着看从左到右依次加1，竖着看，从上到下依次加10。

师：注意观察，知道依次加的顺序。

生3：我还发现了第1列的数个位都是1，第2列的数个位都是2，第3列的数个位都是3……

师：眼睛真亮！那我们也可以怎么说？（教师手指着列数与个位上的数）

生3：也就是列数和每列的个位上的数一样。

师：谁能说得既到位又简洁？

生4：我发现行数与十位上的数相同。

师：同意吗？

生5：不行，第一行十位上没东西，第二行十位上的数都是1，第三行十位上数的都是2。

师：那这又可以怎么说呢？

生5：也就是行数比十位上数多1。

生6：斜着看，都加11。

师：这个不明确，这位同学斜着是从左上到右下。（教师指明左上、右下、右上、左下的四个方向位置）

生6：斜着，从左上到右下依次加11。

生7：从右上到左下是依次加9……

学生之间的思维碰撞，互动交流，让他们的思考得到了进一步深入。

五、引导质疑问难，让思考更明确

在日常教学中，教师经常会依循自己的经验，围绕教学目标为学生预设问题，人为地为学生搭建解决问题的支架，从而达到预设的教学目标。使学习走向深入的一个重要环节是学会质疑——即发现问题和提出问题。教学应该启发、鼓励学生提出自己的问题，让学习突破概念文本、公式法则等的约束，从研究学生的真实困惑开始，触动学生数学的理性思考,从而循着学生的思考探究知识背后蕴含的道理。

如，罗老师执教《长方体的体积》一课时，上课伊始，罗老师就问：“今天我们要学习的是长方体的体积，谁知道长方体体积怎么计算吗？”家长提前告知、书本自学、课外班接触等各种缘由，几乎全班学生都举手表示知道长方体的体积计算公式。学生都会了，这节课学什么呢？教学的任务如果只是提供现成的、僵化的、形式的知识，仅限于知道“长方体的体积＝长×宽×高”公式化的表达，那就不是真正的学习。笔者认为，教学更应该关注学生对知识产生的好奇心，鼓舞并引导学生从对知识产生困惑开始学会学习。只见罗老师一反常态，对班上的学生说：“今天我们本来要学习的是长方体的体积，但是你们都会了，那就收拾东西准备下课吧。”突如其来的下课，让学生不禁好奇，主动后退一步自我反思，并叩问自己“这节课学什么”，从而促发学生根据已知的内容来思考，进而提出疑问：“我们只知道计算公式，但不知道公式是怎么推导出来的？为什么这样计算？”关键的质疑，推动着学生对长方体体积的公式提出真实的困惑，进一步对已知的公式进行批判性思考：“我们只是知道长方体的体积计算公式，但不知道为什么要这样算？”“为什么长方体的体积＝长×宽×高呢？”产生迫切的需求：“我们还需要深一步理解。”……

因此，课堂上要引导学生质疑问难，在提出真实问题的过程中，学生已不满足于仅仅知道公式，而是主动寻求深入学习的突破口，质疑长方体公式的形成之“理”，开启探究知识本质的学习。真正的学习就此开始，伴随着问题的产生，促发学生的学习从公式化的“是什么”走向追求真理的“为什么”，激励学生进行深度思考。