凸显内核 丰盈思想——《打电话》教学例谈

文|夏向阳 张磊铭

一、教材分析

人教版五年级下册《打电话》属于综合与实践内容，设置的目的在于培养学生综合运用有关知识与方法解决实际问题，培养学生的问题意识、应用意识和创新意识，积累活动经验，提高学生解决现实问题的能力。基于此，本课时的教学目标定位：

1.创设学生熟悉的“打电话”生活情境，指导学生用画图、列表格等方式，找到“打电话”的最优方案，经历有目的、有设计、有步骤、有合作的实践活动。

2.进一步体验数学与生活的密切联系，经历针对具体问题提出设计思路、制定简单方案解决问题的过程，培养学生运用数学知识解决实际问题的能力。

3.用画图、列表格等方式发现事物隐含的规律，体会数形结合、推理、优化、模型等数学思想，进一步培养学生的归纳推理和解决简单实际问题的能力。

二、教学过程

1.阅读理解，自主解决。

师：同学们，四年级上册我们学过了烙饼问题，知道了如何合理安排时间，今天我们要继续学习合理安排时间的问题——打电话。

师：一个合唱队共有7人，暑假期间有一个紧急演出，老师需要尽快通知到每一位队员。如果用打电话的方式，每分钟通知1人，请帮助老师设计一个打电话的合理方案。

师：同学们，从题目中你获得了哪些数学信息？

生1：老师需要通知7人，每分钟通知1人。

生2：需要尽快通知到每一位队员。

师：通知的人数是7人，通知的用时是每分钟1人，通知的要求是尽快。

师：请你根据题目的要求，设计一个打电话的方案。请同学们把方案记录在《学习单》上，比一比谁设计得更合理。

2.展示评价，探究规律。

（1）交流方案，对比优化。

师：请同学们一起来看这位同学的设计方案。

生1：

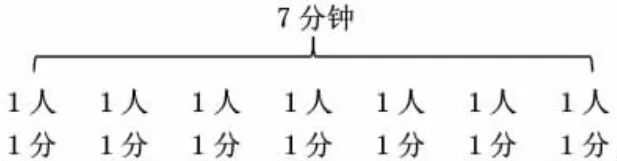
师：这位同学用了7分钟的时间。第1分钟通知第1人，第2分钟通知第2人，这样依次通知，我们就给它取个名字叫逐个通知，也就是一个个通知，一共花了7分钟时间。对他的这种设计方案，同学们有想法吗？

生2：我觉得上面这种方法太慢，我是这样设计的。

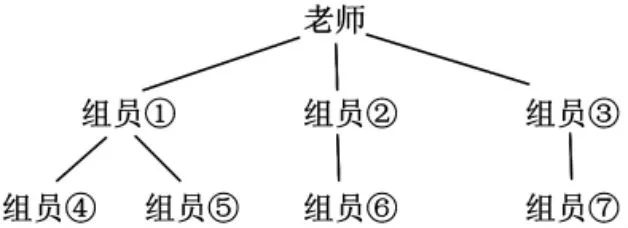
先花3分钟打给组员①、组员②、组员③，打给组员②的时候组员①可以打给组员④。

师：这样设计的方案需要几分钟？

生2：4分钟。

师：这位同学的方法是分成了3个小组进行通知，那么我们就称为分组通知。需要的时间是4分钟。

师：接下来请同学们比较一下这两种方法，想一想为什么分组通知比逐个通知花的时间更少？

生3：先通知的组员可以通知别的组员，比老师一个一个通知组员要快。

生4：我觉得逐个通知就只有老师一个人在打电话，但分组通知是很多人在打电话。

师：说得真好。逐个通知只有老师一个人通知，而分组通知的时候有多人同时在打电话。

师：下面这位同学只用了3分钟，我们一起来讨论一下这位同学的设计方案。

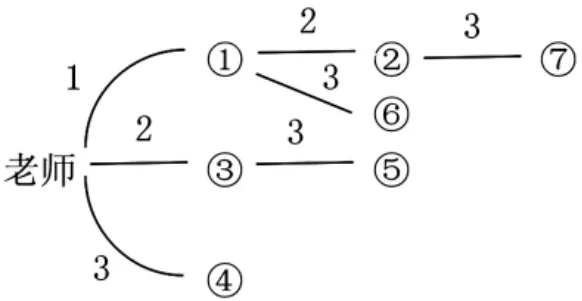
请这位同学结合自己设计的方案向同学们作一下介绍。

生5：老师先打给同学①花费一分钟，第2分钟的时候同学①打给第2个同学，同时老师打给第3个同学，第3分钟的时候接到通知的同学和老师又可以打给4个同学。

师：这位同学的方法你们看懂了吗？我们一起再来回顾一下（略）。

师：有没有比3分钟更少的方案？

生：没有。

师：为什么？

生：每一个人都在打电话，没有人出现空余。

（2）厘清思路，感受优化。

师：这位同学不仅画了图，而且还在线上注明了时间，让我们一看就很清楚。下面老师要提高难度了，请同学们不画图，在头脑中想一想，第4分钟可以通知到几个学生？

生：我觉得可以通知8个人。

师：大家都同意这位同学的想法吗？接下去我们借助图示一起来验证一下。

师：上图显示的和同学们所说的8人是完全一致的。同学们，像这位同学通知的方法我们也取个名字，叫做最优化通知，时间只要3分钟。那么请同学们想想看为什么最优化通知只要3分钟，比分组通知4分钟还少了1分钟，这又是什么道理呢？

生：因为分组通知只是3个人在同时打，出现了有空余的人不在同时打电话，而最优化通知是所有已经知道的人都在打电话，没有空余。

师：说得真好。最优化通知正如这位同学所说的，知道的每个人都在打电话，这样设计的方案时间就会少。

（3）归纳推理，建立模型。

?

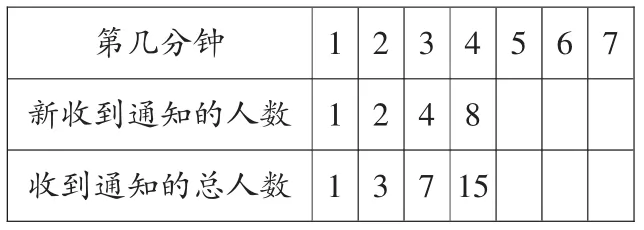
师：谁来回答一下你觉得第5分钟新收到通知的学生人数有几人？

生1：我觉得是12人。

生2：我觉得是16人。

师：她觉得是12人，你觉得是16人。下面我们来进行一下表决，同意12人的请举手，同意16人的请举手。

师：看来同学们都同意16人。那谁来说说看这16人是怎样得到的？你能不能把其中的道理和同学们说一说。

生：人数一直都是在2倍2倍地增加。

师：你能不能说得更加清楚一些？

生：第1次新通知到的人数是1人，第2次新通知到的人数是2人，第3次新通知到的人数是4人，第4次新通知到的人数是8人。

师：所以第5次你觉得是几人？

生：16人。

师：想法和这位同学一样的请举手。老师有一个问题，收到通知的学生总人数第4分钟是15人？为什么第5分钟新收到通知的学生人数是16人？这又是什么道理？

生：因为老师也可以通知1人。

师：第6分钟谁来说一说，收到通知的学生总人数是几人？

生：我觉得是63人。

师：第7分钟新收到通知的学生人数是多少？

（4）探索规律，深化突破。

?

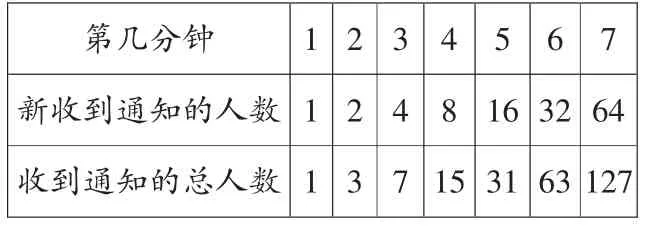
师：看了这个表格之后，刚才同学们说的新收到通知的人数呈2倍的倍数关系递增外，你还有什么新的发现？

生：总人数是乘2加1。

师：请你结合表格说一说怎样乘2加1。

生：1×2+1=3（人），3×2+1=7（人）。

师：所以你就觉得是乘2加1，是吗？那么这个加1是什么意思？

生：多出来的1人是老师通知的学生。

师：下面我们一起来验证一下这位同学的发现。谁能结合7和15来说一说。

生：因为7×2=14，14+1=15。

师：听得明白吗？说得真好。谁能解释一下7×2=14表示什么意思？

生：7是指之前通知到的学生总人数，接下去这7个人都会打电话通知学生，所以一共有7×2=14（人）知道，老师还会再通知1人，所以还要加1人，等于15人。

师：真了不起。从画图到列表你们找到了这样的规律。

生：还有一个规律，新收到通知的人数是前一分钟收到通知的总人数加1。

师：你能不能结合表格说一说？

生：1+1=2，3+1=4，7+1=8……

生：我还找到一个规律。第4分钟新通知的人数是8人，第3分钟收到通知的总人数是7人，8+7=15（人），就是第4分钟收到通知的总人数。

师：这里的7加这里的8正好是15。我们再来找一找。

生：15+16=31（人），31+32=63（人）。

师：你们觉得这个规律成立吗？我们班的同学真聪明，很会动脑筋。

3.应用规律，类比思想。

师：同学们，我们今天这节课学习了打电话，接下来请同学们完成《学习单》上的练习题。

孙悟空去西天取经的路上遇到妖精，于是它每次拔一根毫毛就能变成一个孙悟空，变出的孙悟空每次拔一根毫毛也能变成一个孙悟空，每次变化需要的时间是2秒钟。10秒钟最多能变化出多少个孙悟空？

4.回顾反思，课堂总结。

师：同学们，今天这节课我们学习了打电话的数学问题。请同学们想一想，打电话这一数学问题和我们四年级上册学习的烙饼问题、沏茶问题有什么联系？

师：学了打电话这一数学问题后，你还有什么问题呢？

生1：需要知道他人的电话号码。

生2：需要准备好打电话的方案。

师：同学们，我们打电话采用最优化的方案，前期我们也要做一些准备工作。比如哪位同学打给哪位同学，事先要有一个示意图，这样谁打给谁就很清楚了。

三、教学反思

1.紧扣核心，培养高阶思维。

尽快通知的核心是“每个接到通知的队员都不空闲”，规律的核心是“第n分钟新接到通知的队员数等于前（n-1）分钟内接到通知的队员和老师的总数”。教学时，紧紧抓住这两个核心，借助表格引领学生发现规律，帮助学生理解。在发现规律的过程中，教师要通过观察、思考和交流，提高学生概括、提炼和总结的能力，培养学生的几何直观、推理思想和模型思想，促进学生思维在更高层次上发展。

2.多元表征，彰显数学化。

无论是逐个通知，还是分组通知和最优化通知，都原生态的让学生用自己喜欢的方法尝试解决。学生大胆运用语言、文字、符号、图示、算式等不同的方式来表征自己的思维过程。即使同一种表征方式，也可以有不同的表达形式。如图示法，学生可以画出不同方式的示意图，可以让学生把每一分钟新接到通知的队员用不同的颜色或图形表示出来，也可以直接用序号来表示。把打电话的设计方案抽象成示意图，这实际是一个数学化的过程，有利于培养学生的符号意识，体会数学方法的简约之美，帮助学生形成有序、全面思考问题的品质。