小学数学高段“数与代数”领域中RMI原则的运用

江晨

【摘要】数学教学中关系映射反演原则是非常重要的数学思想，通过反演思维能够把复杂问题映射到简单问题中，从而达到化繁为简、化难为易的目的。它在“数与代数”领域中应用广泛，在数的运算、概念教学、解决问题中都起到培养学生逻辑思维能力，提高学生分析问题和解决问题的能力。

【关键词】RMI原则;数与代数;小学数学

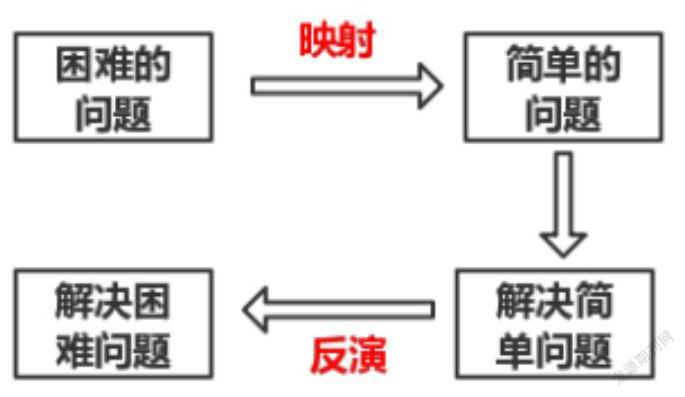
RMI原则是一种实用的数学原则，它是巧妙的把需要解决的复杂问题转化为较简单或者好理解的问题，从而达到解决原来问题的目的。简单来说就是通过问题到问题的映射，从而得到化繁为简，化难为易的目的。可以用思维图来说明如下：

一、RMI原则在小学“数与代数”中的必然性和必要性

在小學数学“数与代数”领域中，存在大量的数的运算的学习。可是现如今虽然从小学一年级开始就在着重培养学生的运算方法，提高学生分析、解决问题的能力，但是到高段之后，依旧存在部分学生计算能力弱，对于复杂问题手足无措的现象。原因可能来自于老师上课形式、教学模式没有起到很好的引导作用。我们对于数与代数领域的教学常常依赖于给学生大量的题型积累，多做多练，达到运算熟练。但这种方法导致学生只重视计算结果，只会做单调题型的计算，对于运算法则和原理了解的不够透彻。课上可能对于算理的分析描述不够，只讲究算法的多样性[]。

而学习数学不能单单学习数学知识，更要了解知识之间的联系，学习数学的精神、思想和方法。数学知识并不是单一没有逻辑的，而是呈网状向外发散，并处处连接、层层递进。在教学的过程中，教师要注重知识的上下承接，新旧联系[]。

RMI原则能够帮助学生养成良好的学习习惯和常态，在学习初期就从片状式知识转为线状式知识。更好的理解掌握并且连接已学习的知识脉络，发现数学知识在生活中的广泛应用，感受学习数学的魅力和兴趣。并且RMI原则能够帮助学生更好的进行分析和处理问题，并培养学生解决问题的方法和策略。

二、概念映射：巧变素材，具化思维

数学概念作为数学知识的思维体现形式，是数学教学中非常重要的一块。能够正确理解灵活运动数学概念，也是掌握数学知识技能，发展数学思维逻辑的大前提。但对于从具体形象思维到抽象思维高速发展的小学生来说，数学概念是不太好理解，是抽象的。很多学生往往通过记忆背诵概念的形式来学习知识，效果往往事倍功半。

（一）概念唤醒，纯化意义

【课例】5年级下册的第4单元——《分数的意义》

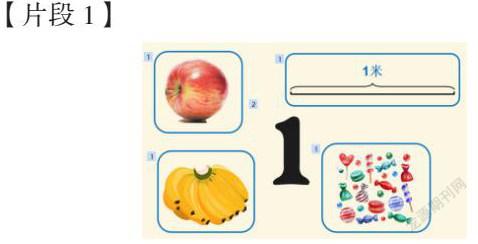
对于单位“1”的定义通过一个小游戏引入

师：游戏名字就叫做“用1说话”。你们准备好了吗？

预设：1个圆;1条线段/一个计量单位;1个菠萝;4个苹果/一堆苹果/一些苹果（用圆圈圈起来）

【分析】

在之前的数学学习中没有提过单位“1”的含义，而五年级开始把可以看作一个整体的物体叫做单位“1”，在这节课中要让学生进一步体会、领悟单位“1”，为什么存在单位“1”。所以重难点在于是对单位“1”的理解。运用RMI原则，把单位“1”的概念映射到现实存在和学过的事物，由此来确定单位“1”的含义。

分数的意义的概念展示

【分析】

在教材中为了帮助学生能够充分建立起分数的概念，通过这样两幅图片来展示分数的产生。这两幅图找到了分数的产生与现实生活的关系，因为需要测量更小的数据和分更小的量，当不能用整数来代表的时候，为了更准确的表示了所需要的结果，于是需要分数[]。把抽象的分数巧妙的映射到现实情境中来，让它有了实际的意义。

【课例】六年级上册第六单元《百分数的认识》

百分数的产生

师：在之前的篮球比赛中，我们班同学奋勇拼搏，战果累累。这是我们班三位主力平时的投篮练习情况。（出示三位学生的投篮总投球数和投中数）如果要出一名同学加入学校的校队，该怎么选择呢？

预设：比较他们的命中率，谁的命中率高选择谁。

师：那该怎么比较呢？

预设：计算每次投篮中，投中的数量占总数量的几分之几。

师：请4人为一小组，算一算谁的投中率比较高。想一想有没有什么好办法能够直接来比较他们的大小？

小组讨论，动手计算比较。引导学生将三个分数通分成分母是100的分数，并由此引出百分数的概念。

【分析】

百分数这个词对学生来说比较陌生，所以在这里创设情境，从学生已有的分数的知识基础上，加以映射，从而根据分数的意义顺理成章的引入百分数。也为之后分数、整数和小数的互换打下基础。

（三）概念提升，拓展广度

【课例】师：生活中有很多百分数，你还在什么地方见过？

展示学生搜集到的含有百分数的句子，并说说百分数的含义。

例如：小学生的近视率为18%。就是说小学生中近视的人数占全体小学生人数的。

初中生的近视率为49%。也就是初中生的近视学生是全部初中学生数量的。

【分析】

三、运算映射：巧联旧知，勾连思维

（一）数数相对，找准关系

如小数乘法3.1×20，可以先让学生利用整数乘法的31×20，得出答案620。再找到积的小数点和两个乘数的小数点的关系，确定积是几位小数。这种方法能够帮助学生快速理解小数乘法如何运算，并且能够运算的又快又对。其实这也是教材推荐的方式，把抽象难懂小数运算的变成熟悉的整数乘法。

在RMI原则中，重要的是找准新知与旧知之间的对应关系，确定好可以映射的对象，映射可以一步也可以几步进行，重点在于把学生不好理解的问题简单化，化为学生已学过熟悉的事物和知识，再反演得出答案。

四、RMI原则后续思考

RMI原则作为一种分析处理问题的重要方法，不止在小学阶段，在之后初中、高中甚至高等数学的学习中都起到非常重要的作用。运用RMI原则选取合适的映射，能够拓展学生的解题思路，降低解决问题的难度。所以，教师在教学过程中，要有意思的联系小学数学的知识体系，鼓励倡导学生利用RMI原则挖掘数学问题的本质信息来解决问题。这能够帮助学生提高数学解题的思想层次，乐于发现数学问题中的核心价值，愿意去探索、归纳、总结。

参考文献：

[1]刘大卫.“RMI”数学思想及其应用初探[M].成阳：成阳师范专科学校学报 （ 自然科学版 ），1998.

[2]戴祥领.RML方法在数学中的应用[M].贵州：遵义师范学院学报，2004.