问题驱动：让学习真实发生

黄肖慧

摘 要：文章针对学法单一、教法单一的小学数学教学现状，提出问题驱动教学方法，让学习真实发生。文章以“等式（一）”的教学为例，阐述了设计核心问题、创造问题提出的情境、进行必要的问题提出策略训练等教学策略在实践中的应用。

关键词：问题驱动;问题提出;问题解决

在日常听课调研中，笔者发现现在的数学课堂存在问题单一、学法单一的问题，学生常常处于浅层的、被动的学习状态。问题单一，就是教师热衷于循着精心安排的教学流程，采用连续的碎问，牵着学生走，学生处于被动接受状态[1]。问题设计往往过细、过窄，当学生的回答是教师所预设的答案时，这个问题的讨论就马上被终止。即便教师提出具有一定开放性的问题，但因没有为学生预留充足的思考时间，客观上也没有促使学生的思维深度和广度产生质的变化。学法单一，就是学生学习的方式呈现个体性，师生之间、生生之间虽有互动，但因缺少引导，缺乏“倾听、思考、表达”的策略支持，信息交流经常处在不畅通状态。从根本上看，这是忽视了学生主观能动性造成的。如果忽视学生的内心需求，学生就会成为被动的信息吸收者;而教师作为引导者、组织者的角色也没有发挥应有的作用。

基于建构主义支架式教学理论，采取问题驱动教学是改善课堂生态的有效策略。教师通过设计驱动性问题，发挥教师前瞻性、递进性的“导”，激发学生实质性思考的“研”，促进深度交流，使学习真实发生。下面以西师大版五年级数学下册“等式（一）”一课的教学为例加以说明。

一、课前思考

（一）教之困

本课是一节概念课，属于小学阶段数与代数领域中“方程”的教学范畴。學生之前已经学习了“用字母表示数”，本课学习的“等量”“等式”概念是代数学习的基础，是学习等式性质、解答方程的必要条件，是培养代数思维的前提。

心理学家罗斯认为，记忆中的种种概念，是以概念的具体例子来表示的，而不是以某些抽象的规则或一系列相关特征来表示的。学生头脑中的典型性范例，常常被称作概念的意象表征或心理表征。如讲到“等量”时，学生的意识中首先出现的是一个直观的例子，而不是它的文本定义。教学中，给“等量”“等式”建立形象直观的表征意义，能降低学生理解和记忆的难度。

此外，等式的意义作为一节独立的课时，在其他版本的小学数学教材是没有的。西师大版教材的处理，有其本身的道理。仅从语义上分析“用字母表示数”“等量”“等式”“方程”等知识点，它们似乎是离散的，只有把“等量”“等式”贯穿“式与方程”的整体教学，其内在的联系和知识结构才会被挖掘出来。在复杂的实际情境中，把实际问题转化为数学问题，把数学问题转化为代数问题，厘清等量关系，建立初步的代数思想，是方程教学的价值内涵，也是本单元学习的一大难点。为分散此难点而安排的本课，其铺路作用是不言而喻的。

（二）学之惑

虽然在解决实际问题后，学生积累了一定的学习经验，但是其建立问题表征的意识不强，思考问题也不够全面[2-3]。而在本课学习中，学生要灵活地对问题表征进行分析，并正确、迅速地收集、处理信息，去除多余的，选择必需的，找到数量之间的相等关系，写出等式。这一连串的步骤，环环相扣，层层推进，正是学习的难点所在。

基于以上分析，本课将结合具体情境，引导学生用多种方式表示等量，让学生知道同一种等量关系可以写成不同的等式。学生在经历用多种方法表示等量关系的探索过程后，会获得提出问题和解决问题的感性经验。在此过程中，学生能初步了解到等量关系在日常生活中是广泛存在的，并初步建立模型思想，形成用数学的眼光观察世界的意识。

二、教学过程

（一）环节一：揭示课题，问题驱动

师：同学们，请齐读课题（等式）。

今天我们一起研究等式，关于等式，你想知道些什么？

生1：什么是等式？

生2：等式有什么用？

生3：有不等式吗？

生4：等式与方程有什么关系……

小结：同学们提的问题都很有价值，有些会在这节课展开研究，有些则会留到后面进一步学习。现在，让我们一起研究“什么是等式” 。

设计意图：本课开门见山地揭示课题，让学生主动提出问题，使学生在较短的时间内明确本课的学习要点和方向，并带着问题走进数学课堂。教师引导学生自主提出问题，给予他们一种绘制自己的学习蓝图的感觉，从而让他们获得更多的学习乐趣与动力。

（二）环节二：任务驱动，引入概念

1.创设情境，小组合作

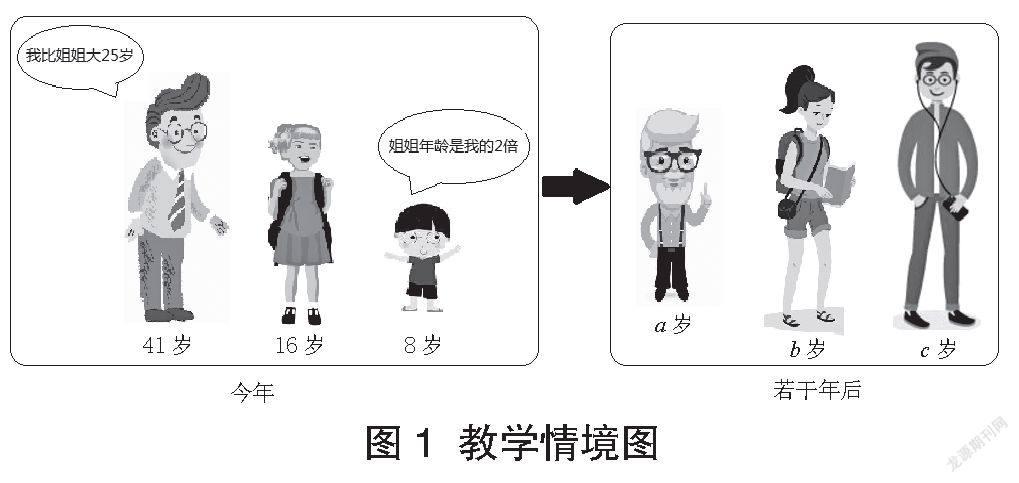
师：请看情境图（如图1），根据图中的数学信息，以四人小组为单位开展活动，完成任务单如图2。

设计意图：美国教育学家布鲁纳曾说，向学生提出有挑战性的问题，可以引导学生发展智慧。在任务驱动教学中，问题串的设计环环相扣，鼓励学生积极思考并提出自己的观点，而多元表征情境中的数量关系，是学生开拓思维、提升能力的重要途径[4]。同时，这使抽象的数量关系可视化，给“等量”“等式”概念建立了直观的形象。

2.分组反馈，揭示概念

（1）学生分组汇报

A.试一试，用文字、画图、算式等方式表示姐姐今年的年龄。

姐姐今年的年龄=爸爸的年龄-25

弟弟的年龄×2=姐姐今年的年龄

16=41-25 16= 8×2 16=8+8

B. b=a-25 b=c+8

C. 16=41-25=8×2=8+8

“今年”，姐姐的年龄有多种表示方式，图与式子、文字之间是对应的，三个式子的结果都相等。“若干年后”，三人年龄未知，字母指向的年龄不是特定的。但是他们之间的数量关系没变，这些式子表示的量也是相等的。

（2）汇总小结

师：如16与41-25、b与c+8，这样的量，大小相等但是形式不同，大小相等的这两个量称为等量（或同量）。

在等量之间加上等号，就成为等式。如16=41- 25，c+8=b。

设计意图：第一个层次，引导学生运用已学的知识对“姐姐今年的年龄”这一数量关系进行多元表征分析，有纯数字的算式、文字、线段图等方式;第二个层次，在理解数量关系的基础上尝试列出含字母的等式;第三个层次，引导学生观察、归纳，发现等式的合理性。

（3）举例巩固

师：你还能从情境图中找到其他的等式吗？请跟同伴说一说。

（4）重新认识等号

师：把b+25=a写成a=b+25，16÷2=8写成8=16÷2，它们还是等式吗？为什么？

生1：还是等式。式子中有等号，意味着等号两边的量相等。

生2：只要等号左右两边的量相等，无论是从左往右看，还是从右往左看，它都是一个等式。

设计意图：大量的例子使学生深入理解了等式的含义，而“把b+25=a写成a=b+25，16÷2=8写成8=16÷2，它们还是等式吗？”这一设问对等式的本质属性进行了更深层次的挖掘。

（三）环节三：多维提问，对比运用

1.判断提问

教师让学生独立完成课本第80页第2题。

小明：除了16+x<18、b+a>c、8x+4b不是等式，其他的都是等式。

师：同学们要向他提问题吗？

生：能说说原因吗，你怎么判断的？

小明：16+x<18中间没有等号，证明左右两边不相等，不是等式。8x+4b没有跟它相等的量，只是一个式子。

小结：如16+x<18、b+a>c这样表示不相等关系的式子，叫不等式。

设计意图：教师在揭示概念之后，进行正反类比是强化理解的有效策略。同时，引导学生提问有着隐性的教育功能。学生多提出与知识本质相关的问题，能加深自己对知识的理解。

2.阅读提问

师：请自行阅读教材第77页例1，关于“什么是等式”，你还有什么疑问？

生1：17=55-38这个等式，还可以表示哪些情境中的等量关系？

师：谁能解决？

生2：商店里有55千克苹果，卖出38千克，还剩下17千克。

总重量-卖出的重量=剩下的重量

生3：航模小组有55位男生，比女生多38人，女生有17人。

男生人数-38=女生人数

生4：妈妈的微信钱包里有零钱55元，爸爸的微信钱包里有零钱38元，妈妈的零钱比爸爸的零钱多17元。

生5：是不是在所有的情境中都能找到等式？

师：这个问题有价值！同学们先在小组里交流自己的看法。

组织学生开展相关的辩论赛。

设计意图：用数学语言进行表达比用一般语言进行表达的难度更高，且这种表达能力并不是与生俱来的。因此，数学学习过程需要把“学习”与“提问”有机融合，教师要营造民主的课堂氛围，通过师生、生生多样化的交流方式，让学生敢问、能问。

（四）环节四：全课总结

1.这节课解决了课程开始提出的哪些问题？

2.我们是怎么学习的？

設计意图：首尾呼应，对开始提出的问题做阶段性小结，引导学生反思学习的过程，这样既能进一步理清知识脉络，也能促进学生个体认知发展。不但促使学生成为知识的消费者，也有助于学生成为知识的创造者，引导学生树立正确的学习观，培养其提出问题、解决问题的能力，使之成为现代社会所需要的综合型优质人才。

三、教学反思

（一）设计核心问题引导学生深度参与学习活动

以问题为核心，就是将课时学习目标分解成若干个小目标，每个小目标以关键问题的形式呈现，即支架问题。每个支架问题再分成若干个子问题，使学生能通过尝试、探索、实验、合作、交流等活动，解决一个个问题，最终沿着问题支架一步步攀升，在问题探究的过程中建构新知识。

（二）提出问题是学生进行有效数学思维活动的桥梁

教学设计要利于学生对数学问题产生疑问，教师设计教学内容要以问题探究为重点，要树立以问题为中心的教学意识，努力激发学生的探究欲望，让学生在问题探究中获得新知识、新思想、新方法。

（三）必要的问题提出策略训练提高学生的问题解决能力

进行问题提出的专项训练，能使教学活动真正做到培养和提高学生分析问题、解决问题的能力，发展学生的智力。

[参考文献]

孙雨澜.“问题提出”的教学研究综述[J].数学教学，2018（3）：17-21，47.

张世武.小学数学教学中培养学生解决问题能力的策略[J].学周刊，2022（1）：136-137.

颜淑兰.小学生数学问题提出的现状与对策[J].亚太教育，2015（25）：13-14.

闫佳洁，于国文.他山之石：ICME-14“问题提出”研究观点综述与教学启示分析[J].教学月刊小学版（教学），2021（9）：57-62.