学生数学符号意识表现的四个维度及其培养方向

于芳

[摘  要] 学生数学符号意识的表现可以划分为四个维度，即理解维度、表征维度、运算维度和推理维度。据此，在培养学生的数学符号意识时，可相应地从以下三个方面展开：形象感知，理解符号的意义内涵;抽象概括，提升符号表征水平;创设情境，运用符号运算推理。

[关键词] 符号意识;理解;表征;运算;推理

朱立明和马云鹏认为，“数学符号意识”，即学习者在思维的引导下，对数学知识与数学符号之间抽象对应关系的一种积极主动的心理认知活动，在通过数学符号的感知与理解、运算与推理、交流与表达等数学思考方式解决数学问题的过程中所表现出来的与数学符号相关的一种数学核心素养[1]。

因此，学生数学符号意识的表现可以从四个维度进行划分和界定。

一、学生数学符号意识表现的四个维度

（一）数学符号理解维度

数学符号的理解是对数学符号的直觉认知，即理解数学符号所蕴含的意义及其使用条件。这是数学学习的基本要求，也是数学符号意识的基本要求。

对数学符号的理解有三种表现水平。

1. 只能理解数字符号、运算符号等，不能理解字母等抽象数学符号的内涵与意义。例如能理解具体的数量3，但是无法理解3a。

2. 能够理解字母的表面含义，但是不能理解字母所具有的一般现实意义。例如知道3a就是3×a，但无法将其与现实情境相联系。

3. 不仅能理解数学符号的内涵和意義，还能理解数学符号与数学知识之间的关联，能够在具体情境与抽象的数学符号之间建立联系。例如不仅知道3a是3个a相加的和，还知道a可以表示长度、质量、单价、速度……

（二）数学符号表征维度

数学符号的表征是理性思维的体现，意味着能够将数学信息用符号系统表示出来。数学符号表征是运用符号进行运算和推理的基础。

数学符号表征有三种表现层次。

1. 能运用数字表征具体数量，也能运用数学符号（字母）表征数（未知数、不确定的数等），对数学符号的表征处于简单模仿阶段。

2. 能运用数学符号表征数量关系。例如能够用含有字母的式子表征一辆公共汽车上人数的变化，或者根据数量关系列出相遇问题求速度的方程等。

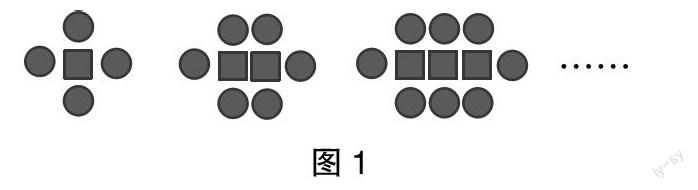
3. 能运用数学符号表征变化规律，也就是能通过探索问题中的变化关系找出问题的隐含规律，并运用数学符号进行表征。例如探索图形排列的规律（图1），并用含有字母的式子表征第n个图形中正方形和圆形个数的关系。

（三）数学符号运算维度

数学符号的运算是数学活动的基本形式，即根据数学概念、定理和运算法则，将数学符号通过计算得出确定结果的过程。

数学符号的运算包含三个阶段。

1. 数字符号运算阶段，学生可以解决具体的数字符号的运算，也就是我们所说的四则混合运算。

2. 符号形式的运算阶段，学生可以在操作层面理解数学符号的运算，但不能理解运算所得到的结果具有一般性。例如学生能够计算3a+4a=7a，但不理解式子中的a可以指代任何有理数。

3. 符号的抽象运算阶段，学生能够从算理的角度理解数学符号运算，可以很好地理解运算所得到的结果具有一般性。也就是学生不仅能够计算3a+4a=7a，还能根据乘法的意义解释这个式子的意义，并知道它的结果具有一般性。

（四）数学符号推理维度

数学符号的推理主要包括代数推理和图形推理。

1. 代数推理，根据运算法则推理出字母式子的值。

如题“已知a=2，b=3，求（ab）2的值”。

2. 几何推理，根据图形关系进行推理。

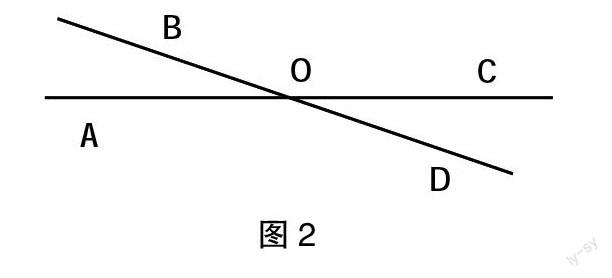
例如“两条直线相交于点O，你能推出∠AOB=∠COD吗？请说明理由（见图2）”。

二、数学符号意识的培养方向

培养数学符号意识可以围绕其四个表现维度展开，也就是要帮助学生理解符号的意义和内涵，学会使用符号表征，运用数学符号进行运算和推理。

（一）形象感知，理解符号的意义内涵

数学符号根据表示的意义可以大致分为元素符号、运算符号、关系符号、结合符号和约定符号等。这些数学符号的使用将伴随学生数学学习的始终，同时也是学生认为数学艰深难懂的重要原因。因此，让学生在形象感知中喜欢、亲近符号，接受和理解符号是培养学生符号意识的首要任务。

1. 直观形象感知

小学阶段的数学符号大多都是十分形象的，或者说是“象形”的，因此让学生通过直观形象去感知符号的意义和内涵能够激发学生的认知兴趣，有助于他们记忆符号的形象和掌握符号的书写方法。

例如在一年级认识数字符号的时候，教师都会带领学生诵读儿歌：1像铅笔，细又长;2像小鸭，水中游;3像耳朵，两道弯;4像小旗，迎风飘……

还有“=”“>”“<”，这些关系符号也是非常形象的。“=”就是两条等长的平行线段，“>”“<”则是大头（开口）对着大数，小头（尖头）对着小数。

2. 动态形象感知

虽然很多数学符号都如同象形文字一样简洁、生动、形象、传神，但要帮助学生深刻地理解其内涵还需要以动态演示的方式来呈现它们的产生过程。

例如加、减、乘、除四种运算符号。加号可以通过先画一横，再移来一竖的演示让学生理解它蕴含着的“合并”“增加”的意思。减号的演示过程则正好相反，学生能看出其表示“去掉”“减少”的意思。乘号就是把“+”转动45度，表示这是特殊的加——同数连加。除号呢？中间一横表示平均分，上下各一点，表示每份分得同样多。

约等号、不等号等也可以用动态演示的方法帮助学生理解。等于号弯一弯，表示有点不好意思，只是大概相等哦;等于号添条斜杠，就表示根本不相等，划掉吧。

数学符号如此简洁、优美，教师要用好数学符号的简约记忆功能、辅助理解功能，重视让学生通过形象感知来理解符号、欣赏符号。

（二）抽象概括，提升符号表征水平

培养学生的符号意识，本质上是培养学生的数学抽象能力，而要提升学生的符号表征水平，也应当从抽象概括入手。

1. 抽象概括，建立数的符号表征

（1）数字符号表征

小学生入学伊始首先要学习和认识的就是数字符号，也就是对数的认识和运用。数概念的形成过程就是一个抽象概括的过程，它舍弃了一切非数量关系的内容（大小、颜色、材质等），只保留了量的抽象结果。

学生在学习数字符号的过程中，要反复经历从直观到抽象、从具体到概括的认知过程。例如在一年级的“数一数”教学中，学生数图片中的多种物体，接着把所有被数的数量相同的物体抽象为对应的圆点，最后将圆点抽象为对应的数字符号。

（2）数学符号表征

学生从一年级就开始接触类似“△+3=8”这样的问题，随着学习经验的积累，在不断地抽象概括中学生会慢慢领悟和接受用“△”“☆”等符号表征特定的数或某个范围内的数，进而理解用字母表示未知数、不确定的数。

2. 对比分析，抽象概括数量关系

学生学习和掌握用数学符号表征数量关系要经历两个过程，首先是抽象和概括已有的公式、定律，其次是提炼数量关系并用數学符号表征。

（1）转换符号，抽象概括公式、定律

学生在探究活动中得到图形的周长、面积等公式后，需要将文字公式写成字母公式，这是一个将语言文字表述转换成数学符号表征的过程。同样地，在学习运算定律的时候，教师也会引导学生将发现和总结的运算定律转换成字母式子来表示。

虽然在上述教学活动中，将语言表述转换成字母式子并不是教学的重点，但我们要知道每一次字母式子的书写和运用都有利于学生符号意识的发展。在运用这些字母式子（公式）的过程中，学生知道每一个字母背后的含义，明白字母能表示整数、小数、分数，感受到数学符号表征的简洁和概括。

（2）对比分析，抽象概括数量关系

如果说学生用字母式子表示公式仅仅是一个表征方式转换的过程，那么他们在学习用字母式子表示数量关系时需要通过对比分析，转变对数学符号的认知，学会通过符号表征抽象概括数量关系。

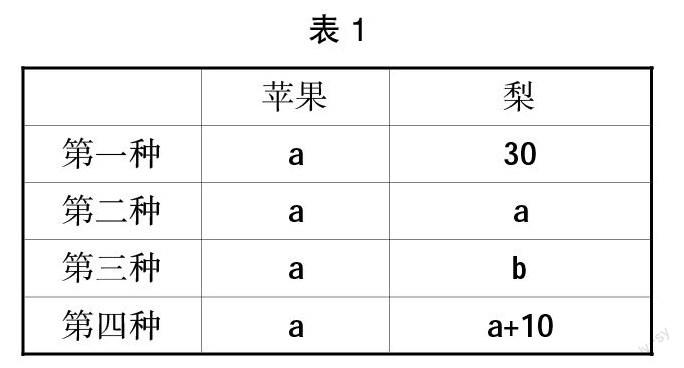
例如教师在教学“用字母表示数量关系”时，可以创设这样的教学情境：现有一箱苹果，数量我们暂不能确定，可以用字母a表示;还有一箱梨比苹果多10个，该如何表示梨的数量呢？

学生整理几种表示方法（见表1）：

全班交流对比分析后，能够理解表示梨的个数的最好方法是第四种，因为它能体现梨和苹果之间的数量关系。第二种方法中，苹果和梨的数量用相同的字母表示，意味着在同一情境下它们的数量相同;第三种方法中，苹果和梨的数量所用字母不同，表示它们的数量不同，但未能反映出梨比苹果多10个的重要信息。

有了前面的学习基础，学生在后续学习列方程解决问题等内容的时候，就能够轻松自如地实现数学符号语言和日常语言的转化，即能将日常语言叙述的数量关系或空间形式转化为数学符号语言。

3. 提炼关系，用数学符号把握变化规律

运用数学符号表征变化规律是小学阶段数学符号表征的最高水平，达到这一表征水平的关键是能够根据规律提炼数量关系，它是用数学符号表征数量关系的延续和提升。

例如在探究多边形内角和与边数的关系时，首先要思考把多边形内角和问题转化成求若干个三角形的内角和问题;接着思考每个多边形能转化成几个三角形;最后是根据三角形的内角和求出多边形的内角和。这其中蕴含着的规律也就是它们之间的数量关系。因此，在教学中教师要引导学生层层剖析其中的数量关系，第一层数量关系是多边形的边数减少2就是它划分成的三角形个数;第二层数量关系是有多少个三角形就有多少个180°累加。理清楚了这两层数量关系，就能够用数学符号表征这其中的规律了。

（三）创设情境，运用符号运算、推理

运用数学符号进行运算和推理是符号意识发展到较高水平的体现，义务教育阶段一般在第三学段（7—9年级）将这一能力纳入考查要求，但并不是说小学生就不能体验“使用符号可以进行运算和推理，得到的结果具有一般性”。如果教师能够创设恰当的数学情境，那么学生还是能够获得一定的感悟。

五年级学生学习了“用字母表示数”之后，立即展开了“多边形的面积”的学习，这一单元中的平行四边形、三角形以及梯形面积公式的推导过程，以及后续的圆面积公式的推导过程，就都运用了符号进行运算和推理。

在“用字母表示数”单元，我们还可以设计下面的数学小魔术：“请你想一个整数，把它乘3加9，再把结果乘3减27。只要你说出计算结果，我能马上写出你想的整数是多少。”

先让学生尝试，教师每次都能准确写出学生心里想的数，让学生惊讶不已，然后引导学生用字母式子解密。

“设所想的数为x，则（3x+9）×3-27=9x+27-27=9x。”

只要计算正确，结果一定能被9整除，将计算结果除以9，就是对方所想的数。

上述教学内容，不仅能极大地增强学生的学习兴趣，还能让他们体会引入数学符号的必要性，并感受到“符号的使用是数学表达和进行数学思考的重要形式”。

参考文献：

[1]  朱立明，马云鹏. “数学符号意识”研究：内涵与维度[J]. 教育理论与实践，2015（32）：6-8.